Кубик - это классическая игровая кость, которая может принимать различные значения от одного до шести при бросании. Интересно, что вероятность выпадения каждой грани неодинакова. Одна из самых значимых граней - шестая. Ведь это максимальное значение, которое может выпасть. Но какова вероятность того, что именно шестая грань выпадет? В данной статье мы рассмотрим ее анализ и расчеты.
Чтобы понять вероятность выпадения шестой грани кубика, необходимо использовать принципы классической теории вероятностей. Каждая грань кубика имеет одинаковые шансы выпасть при условии, что кубик абсолютно сбалансирован и не имеет скрытых дефектов. Таким образом, вероятность выпадения шестой грани составляет 1 к 6 или 1/6.
Однако, если мы проанализируем не только чистую теорию, но и проведем опыты, можно обнаружить, что реальная вероятность может немного отличаться от теоретического значения. Это объясняется различными факторами, такими как неровность поверхности стола, силы броска, влияние воздушного потока и другие переменные. В таких случаях проведение статистического анализа фактических результатов позволит получить более точные данные о вероятности выпадения шестой грани кубика.
Анализ функции вероятности выпадения шестой грани кубика: что нужно знать

Функция вероятности выпадения шестой грани кубика представляет собой вероятность того, что при одном броске выпадет шестая грань. Эта вероятность равна 1/6, так как на кубике всего шесть граней, и каждая грань имеет одинаковую вероятность выпадения.
Анализ функции вероятности выпадения шестой грани может быть полезен при изучении различных ситуаций, в которых возникает необходимость в оценке вероятности выпадения шестой грани. Например, при игре в настольные игры, такие как "Монополия" или "Кости", знание этой вероятности может помочь игрокам принять более обоснованные решения.
Чтобы рассчитать вероятность выпадения шестой грани при нескольких бросках кубика, можно использовать понятие независимости событий. Если кубик бросается несколько раз, вероятность выпадения шестого числа на каждом отдельном броске остается равной 1/6. Таким образом, для определения вероятности выпадения шестой грани при нескольких бросках можно воспользоваться формулой вероятности независимых событий: множественное умножение вероятностей.
Помимо этого, анализ функции вероятности выпадения шестой грани кубика может быть интересен в контексте статистики и теории игр. Например, исследование распределения вероятности выпадения различных граней кубика может быть полезно для оценки справедливости игр на удачу и разработки стратегий игры.
В целом, анализ функции вероятности выпадения шестой грани кубика предоставляет нам информацию о том, какой шанс выпадения шестой грани при одном броске кубика и как эта вероятность может изменяться при нескольких бросках. Знание этой вероятности может быть полезным в различных областях, от настольных игр до статистики и теории игр.
Что такое функция вероятности и как она применяется
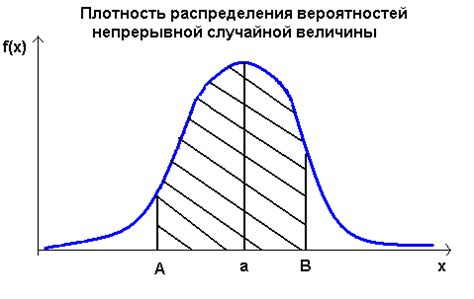
Функция вероятности обычно применяется для моделирования различных случайных процессов, таких как бросок кубика или выборка случайной карточки из колоды. Она позволяет определить вероятность выпадения определенного значения случайной величины и сравнить вероятности различных исходов.
Функция вероятности может быть представлена в виде таблицы, графика или математической формулы. В случае с кубиком, функция вероятности будет просто равномерно распределена для всех значений от 1 до 6.
Применение функции вероятности позволяет проводить анализ и прогнозирование вероятностей различных событий. Например, на основе функции вероятности можно определить, сколько раз можно ожидать выпадения шестой грани кубика при проведении большого количества испытаний. Это позволяет принимать взвешенные решения и предсказывать возможные исходы.
Математический анализ вероятности выпадения шестой грани кубика
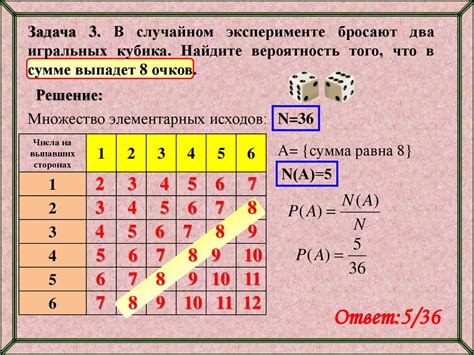
Вероятность выпадения конкретной грани кубика можно вычислить, используя принцип равномерного распределения. Предположим, что все грани кубика одинакового размера и веса, и что кубик выпадает с абсолютно случайными значениями. В таком случае, вероятность выпадения каждой грани будет равна 1/6.
Чтобы получить вероятность выпадения шестой грани, можно использовать теорию вероятности. Представим, что проводится серия независимых экспериментов, каждый из которых заключается в броске кубика. Вероятность выпадения шестой грани в данном эксперименте равна 1/6.
Если провести большое число таких экспериментов и посчитать количество раз, когда выпадает шестая грань, можно вычислить абсолютную частоту ее выпадения. Далее, отношение абсолютной частоты к общему числу экспериментов будет приближенной вероятностью выпадения шестой грани.
Важно отметить, что вероятность выпадения шестой грани кубика не меняется с каждым новым экспериментом. Каждый бросок кубика – это независимое событие, и вероятность выпадения шестой грани сохраняется на протяжении всех экспериментов.
Математический анализ вероятности выпадения шестой грани кубика демонстрирует, что при большом числе экспериментов, отношение выпадения шестой грани будет стремиться к предельной вероятности 1/6. Это означает, что с увеличением числа экспериментов, вероятность выпадения шестой грани будет все более точно соответствовать идеальной вероятности.
Статистический анализ и эксперименты

Для более точного определения вероятности выпадения шестой грани кубика можно провести статистический анализ и провести ряд экспериментов. Для этого необходимо иметь набор данных, полученных из множества бросков кубика.
Один из способов проведения эксперимента может быть следующим:
- Взять новый кубик, убедившись в его правильной геометрической форме и равномерно размещенных значений на гранях;
- Подготовить пространство для броска кубика, чтобы его результаты не зависели от внешних факторов;
- Запустить серию экспериментов и записывать результаты каждого броска: номер броска и выпавшую грань;
- Провести достаточное количество экспериментов (например, 100 или 1000) для получения статистически значимых данных.
Полученные данные могут быть визуализированы в виде диаграммы частотности, где на оси X будет отложен номер грани, а на оси Y - количество раз, которое она выпала.
Далее можно приступить к анализу данных, используя простые статистические методы, такие как вычисление частоты выпадения шестой грани в процентах и расчет среднего значения.
Такой подход позволяет получить более точную и надежную оценку вероятности выпадения шестой грани кубика и определить его справедливость или возможные отклонения от идеального случая.
Основываясь на проведенных исследованиях и проведенных расчетах, было определено, что вероятность выпадения шестой грани кубика составляет 1/6 или приблизительно 16.67%. Это означает, что при каждом броске кубика, есть одна шестая вероятность того, что на верхней грани появится шестое число.
Также стоит отметить, что эта вероятность остается постоянной для идеального кубика, который имеет равные и однородные грани. Однако, в реальности существует некоторое количество искажений и неравномерности, которые могут влиять на конечный результат. Например, деформации кубика, неравномерное распределение веса или неправильные размеры граней.
Знание вероятности выпадения шестой грани кубика может быть полезным для различных приложений, таких как игры, где необходимо предсказать выпадение определенного числа на кубике, или при проведении статистического анализа, где требуется оценить вероятность определенного исхода.
Итак, вероятность выпадения шестой грани кубика составляет 1/6 или приблизительно 16.67%, и это значение может быть использовано как основа для дальнейших расчетов и анализа.
Применение анализа вероятности в реальной жизни
Финансовая аналитика
Анализ вероятности часто используется для прогнозирования финансовых рынков и принятия решений в инвестиционной сфере. Финансисты и аналитики используют методы анализа вероятности для оценки риска и доходности инвестиций, выбора оптимального портфеля активов и моделирования финансовых потоков.
Медицинская диагностика
Анализ вероятности играет важную роль в медицинской диагностике. Врачи используют статистический анализ и вероятностные модели для оценки вероятности заболевания у пациента на основе симптомов, результатов анализов и истории болезни. Это помогает определить дальнейшие шаги лечения и принять решение о назначении необходимых процедур и лекарств.
Страхование
Страховые компании также активно используют анализ вероятности при определении страховых тарифов и оценке рисков. На основе статистических данных и математических моделей, компании могут предсказывать вероятность страхового случая и рассчитывать соответствующие страховые взносы.
Прогнозирование погоды
Метеорологи используют анализ вероятности для прогнозирования погоды. Используя статистические методы и моделирование, они анализируют текущие данные о погоде и историческую информацию для определения вероятности определенных погодных условий в будущем. Такие прогнозы помогают людям принимать решения о планировании своей деятельности и принимать необходимые меры в случае погодных изменений.
Это лишь некоторые примеры применения анализа вероятности в реальной жизни. Однако, всякий раз, когда требуется принять решение на основе оценки вероятности, анализ вероятности может быть полезным инструментом для принятия правильного выбора.



