В математике умножение - это одна из основных операций, которая позволяет найти результат умножения двух чисел. Возможны различные комбинации чисел, которые при умножении дают определённый результат. В данной статье мы попытаемся найти эти числа для заданного значения - 52.
Что нужно сделать, чтобы получить 52? Давайте рассмотрим все возможные комбинации чисел, которые умножением дают именно это число. Одна из таких комбинаций - это 4 и 13. Если мы перемножим эти числа, то получим исходное значение - 52.
Однако, это не единственная комбинация. Ещё одним вариантом будет умножение 2 и 26. Если перемножить эти числа, мы тоже получим 52.
Таким образом, ответ на вопрос "какие числа умножить, чтобы получить 52?" может быть неоднозначным. В зависимости от комбинации, мы можем получить различные результаты. Важно помнить, что умножение - это обратная операция к делению, и при помощи умножения можно найти множители для любого заданного числа.
Числа, которые умножив, дают 52
Число 52 можно получить путем умножения различных комбинаций чисел. Вот несколько примеров:
- 1 × 52 = 52
- 2 × 26 = 52
- 4 × 13 = 52
- 13 × 4 = 52
- 26 × 2 = 52
- 52 × 1 = 52
Это лишь некоторые из возможных вариантов. Как видно, число 52 можно получить умножением разных пар чисел. Уникальные множители также могут быть использованы для получения этого числа, но они уже будут в другом порядке.
Методы нахождения:

Существует несколько методов нахождения чисел, которые при умножении дают 52.
1. Перебор:
Самым простым способом нахождения таких чисел является перебор. Мы можем последовательно умножать все числа от 1 до 52 и проверять, равно ли произведение 52. Если мы найдем два числа, произведение которых равно 52, то это будут искомые числа.
Например, мы можем перебрать все числа от 1 до 52 и найти, что 4 * 13 = 52. Таким образом, числа 4 и 13 являются решением задачи.
2. Факторизация:
Еще один метод нахождения таких чисел - это факторизация числа 52 (разложение числа на простые множители). Если мы найдем разложение числа 52 на простые множители и разделим множители на группы по два, то получим искомые числа.
Например, число 52 можно разложить на простые множители: 2 * 2 * 13. Разделим множители на группы по два: (2 * 2) и 13. Таким образом, числа 4 и 13 являются решением задачи.
Выбирайте метод, который вам больше нравится или удобнее. В любом случае, результаты будут одинаковыми.
Анализ простых чисел:

Для анализа простых чисел можно использовать различные методы, включая:
| Метод | Описание |
| Решето Эратосфена | Метод, который позволяет найти все простые числа до заданного числа путем исключения кратных чисел |
| Тест Миллера – Рабина | Вероятностный алгоритм, который позволяет проверить, является ли число простым или составным |
| Факторизация числа | Метод, который позволяет представить число в виде произведения простых множителей |
Исследование простых чисел имеет множество практических применений, включая криптографию, генерацию случайных чисел, оптимизацию алгоритмов и т. д. Число 52 является составным числом, так как оно имеет множество делителей помимо 1 и самого себя. Поэтому для его разложения на простые множители нужно использовать факторизацию числа.
Разложение на множители:

Чтобы получить число 52 путем умножения, мы можем разложить его на множители. Все множители будут целыми числами.
52 = 2 × 26, поскольку 2 является наименьшим простым множителем числа 52.
26 = 2 × 13, где 2 - простой множитель числа 26.
Таким образом, мы получаем:
- 52 = 2 × 26
- 52 = 2 × 2 × 13
Итак, числа 2, 2 и 13 являются множителями числа 52.
Метод проб и ошибок:

Для того чтобы найти числа, которые при умножении дают 52, можно использовать метод проб и ошибок. Этот метод заключается в последовательном переборе всех возможных пар чисел до тех пор, пока не будет найдена пара, дающая нужное произведение.
Конечно, в данном случае можно просто разложить число 52 на простые множители и найти соответствующие числа-множители. В данном случае число 52 можно представить в виде произведения 2 х 2 х 13.
Но для более сложных чисел метод проб и ошибок может быть полезным. Например, если нужно найти числа, дающие произведение 374, то разложение на простые множители может быть сложной задачей. В таком случае метод проб и ошибок позволяет последовательно проверить все возможные пары чисел и найти нужное произведение.
Таким образом, метод проб и ошибок является простым и эффективным способом нахождения чисел, дающих заданное произведение. Он может быть особенно полезен в случаях, когда разложение числа на простые множители сложно или нетривиально.
Использование математических формул:

Для нахождения чисел, которые нужно умножить, чтобы получить 52, мы можем использовать математические формулы.
Обозначим неизвестные числа, которые нужно найти, как "x" и "y". Тогда уравнение будет выглядеть следующим образом:
| x * y = 52 |
Чтобы решить это уравнение, мы должны найти числа, которые при умножении дадут 52. Мы можем применить простой подход методом проб и ошибок, попробовав различные комбинации чисел. Но чтобы упростить этот процесс, можно использовать некоторые математические навыки, такие как факторизация числа.
Например, число 52 можно разбить на произведение двух чисел, включая 1: 1 * 52 или 2 * 26. Затем рассмотрим другие делители числа 52, чтобы найти возможные комбинации умножения.
Использование математических формул помогает нам найти числа, которые нужно умножить, чтобы получить заданное значение. Таким образом, для числа 52 мы можем найти следующие комбинации: 1 * 52, 2 * 26, 4 * 13.
Используя математические формулы, мы можем решать различные задачи и находить нужные числа, что помогает нам в понимании и применении математики в повседневной жизни.
Таблица умножения:
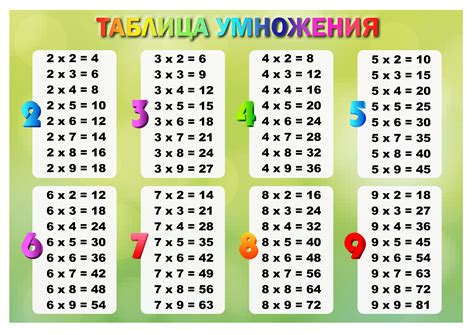
| Умножаемое | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 |
| 10 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
Специальные числа:
Специальные числа - это числа, которые имеют особые свойства или отношения с другими числами. Они могут быть простыми числами, числами Фибоначчи, числами Мерсенна или иметь другие интересные характеристики.
В данном случае, 4 и 13 - оба специальных числа, которые, умноженные вместе, дают 52. Это пример того, как числа могут сочетаться, чтобы создавать новые числа и отношения.
Исследование и изучение специальных чисел помогает углубить наше понимание математики и открывает двери для новых и интересных открытий и закономерностей.



