В мире математики существует множество вопросов, которые приходится разгадывать и искать ответы. Одним из таких вопросов является: "Что умножить на что, чтобы получить 3?". Этот вопрос может показаться простым на первый взгляд, но решение его не так уж и просто.
Чтобы найти ответ на этот вопрос, нужно вспомнить, что умножение является одной из основных арифметических операций. Оно позволяет нам увеличивать число в несколько раз путем складывания его с самим собой несколько раз. Но какое же число нужно взять и сколько раз нужно его складывать, чтобы получить 3?
Для начала, давайте вспомним основное свойство умножения: любое число умноженное на 1 остается без изменений. Из этого следует, что если мы умножим число на 1, то получим то же самое число. Однако, если нам нужно получить число 3, это означает, что нам нужно умножить число на значение больше 1.
Методы умножения
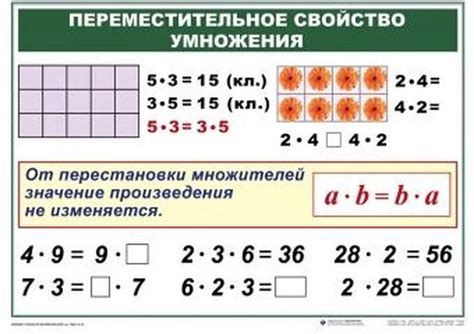
Умножение в столбик
Метод умножения в столбик является основным и наиболее простым способом умножения чисел. Для его применения необходимо записать множители столбиком, выровняв их по разрядам, и последовательно умножать каждую цифру первого множителя на каждую цифру второго множителя, начиная с младших разрядов.
Умножение в столбик с переносом
Метод умножения в столбик с переносом также основан на умножении каждой цифры первого множителя на каждую цифру второго, однако он позволяет выполнять вычисления с переносом разрядов. Необходимо записать множители столбиком, выровнять их по разрядам и начать вычисления с младших разрядов, перенося "лишние" разряды при необходимости и складывая полученные произведения.
Умножение на простые числа
Умножение на простые числа может быть упрощено путем использования известных свойств простых чисел. Например, умножение на 2 эквивалентно сдвигу всех разрядов числа на одну позицию влево, а умножение на 10 - добавлению нулей в конец числа.
Умножение при помощи дополнения до 10
Метод умножения при помощи дополнения до 10 позволяет упростить умножение чисел, близких к 10 или ее кратным. Для этого необходимо найти разность каждого множителя с 10, умножить эти разности на другой множитель и затем сложить полученные произведения с произведением разностей.
В зависимости от ситуации и требований, различные методы умножения могут быть более удобными и эффективными. Важно понимать, что любой из них позволяет достичь правильного результата при правильном применении и выполнении всех вычислений по правилам арифметики.
Простые числа

Простые числа играют важную роль в математике и криптографии. Большие простые числа, например, используются при генерации шифров и защите информации. Однако задача поиска простых чисел и определения их свойств является сложной и до сих пор активно исследуется учеными.
Известно, что простые числа распределены неравномерно, и их количество растет по мере увеличения числового ряда. Например, в интервале от 1 до 100 существует всего 25 простых чисел, а в интервале от 1 до 1000 их уже 168.
Число 2 является единственным четным простым числом, а все остальные простые числа нечетные. Интересно отметить, что сумма всех простых чисел тоже является бесконечной и беспорядочной.
В математике существует несколько алгоритмов и методов для определения простоты числа. Самым известным из них является тест на простоту по Ферма, который основан на малой теореме Ферма и позволяет проверить простоту числа на основе его делителей.
Простые числа играют важную роль не только в математике, но и во многих других областях науки и техники. Их изучение помогает улучшить понимание многих сложных задач и алгоритмов, а также находить новые применения в различных сферах деятельности.
Дроби и натуральные числа
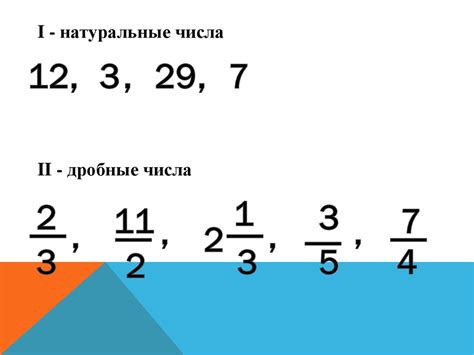
Умножение дробей и натуральных чисел может быть несколько сложнее, но совершенно возможно. Чтобы получить 3, нам нужно подобрать такие числа, которые, будучи перемноженными, дают именно такой результат.
Например, можно умножить число 1 на число 3. Получится в точности то же число, которое мы хотели получить.
Кроме того, можно воспользоваться ситуацией, когда одно из чисел равно 0. Умножив любое число на 0, мы всегда получим 0. Но так как в данном случае мы хотим получить 3, то это не подходит.
Другой подход - это разложение числа 3 на его простые множители. Число 3 является простым числом, поэтому его множители это только само число 3. Тогда мы можем умножить число 3 на 1, чтобы получить 3.
Важно понимать, что результат умножения дроби и натурального числа может быть как натуральным числом, так и дробным. В данном случае мы рассматриваем только натуральные числа и дроби вида 1/число, поэтому получаем результатом только натуральное число 3.
Комбинаторика и матрицы

Комбинаторика предоставляет нам инструменты для подсчета различных комбинаций элементов. В данном случае, нам нужно найти два числа, которые при умножении дают 3. Используя комбинаторику, мы можем перебрать все возможные комбинации чисел и найти нужные нам значения.
Матрицы позволяют нам представлять числа и их комбинации в виде таблицы. Мы можем использовать матрицы для систематического подсчета всех комбинаций чисел и их умножения, чтобы найти нужные нам значения.
Давайте представим числа в виде матрицы:
| 1 | 1 | | 3 | x |
Матрица состоит из двух строк и двух столбцов. Здесь мы заменяем одно из чисел переменной "x". Нам нужно найти значение "x", при котором произведение чисел будет равно 3.
Умножая элементы матрицы, мы получаем следующее уравнение:
1 * 1 + 3 * x = 3
Решая это уравнение, мы найдем значение "x", которое при умножении на 3 даёт 3.
Таким образом, комбинаторика и матрицы позволяют решить задачу нахождения чисел, которые при умножении дают 3, систематически и эффективно.
Алгебраические методы

Для решения этой задачи необходимо воспользоваться свойствами алгебры и анализа. Рассмотрим следующие подходы:
1. Положительные числа:
3 можно представить в виде произведения двух положительных чисел: 3 = 1 * 3.
Таким образом, одним из вариантов будет умножение числа 1 на число 3.
2. Отрицательные числа:
3 также можно представить в виде произведения отрицательного числа на отрицательное число: 3 = (-1) * (-3).
Таким образом, другим вариантом будет умножение числа -1 на число -3.
Алгебраические методы позволяют найти решение различных задач, включая задачу о нахождении чисел, при умножении которых результат будет равен определенному числу.
Иррациональные числа
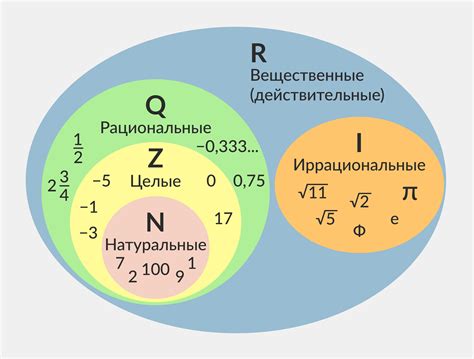
Одно из самых известных иррациональных чисел - это число π (пи), которое равно отношению длины окружности к ее диаметру. Число π является бесконечным и непериодическим десятичным числом, что делает его иррациональным.
Еще одним примером иррационального числа является число √2 (квадратный корень из 2). Это число не может быть представлено в виде десятичной дроби или обыкновенной дроби и является бесконечным и непериодическим десятичным числом.
Иррациональные числа играют важную роль в различных областях математики, таких как геометрия, алгебра, анализ и теория вероятностей. Они помогают уточнять и развивать наши представления о числах и их свойствах.
Свойства иррациональных чисел:
- Иррациональные числа не могут быть точно представлены в виде десятичной дроби;
- Иррациональные числа не могут быть точно представлены в виде обыкновенной дроби;
- Иррациональные числа являются бесконечными и непериодическими;
- Сумма или произведение иррационального числа и рационального числа всегда является иррациональным числом;
- Иррациональные числа расположены на числовой прямой между рациональными числами.
Иррациональные числа представляют собой важный аспект математики и имеют множество интересных свойств. Изучение иррациональных чисел позволяет лучше понять природу чисел и их взаимосвязи.
Специальные формулы

Есть несколько специальных формул, которые позволяют умножить разные числа, чтобы получить 3. Вот некоторые из них:
- 1 * 3 = 3
- 3 * 1 = 3
Как видите, самая простая формула - это умножение числа 1 на число 3. Также можно умножить число 3 на число 1 и получить тот же результат. Эти формулы применимы во многих ситуациях и могут быть полезными в решении различных задач.
Также существуют другие формулы, которые позволяют получить 3, но они сложнее и менее распространены. Например:
- 2 * 1.5 = 3
- 6 * 0.5 = 3
Эти формулы требуют использования нецелых чисел или чисел с плавающей точкой, что может быть не всегда удобно. Однако, они тоже могут быть полезными в определенных ситуациях.
Так что, в зависимости от конкретной задачи, вы можете выбрать одну из этих формул или использовать другую специальную формулу, чтобы умножить числа и получить 3.



