Когда речь идет о квадрате, одной из его основных характеристик является его площадь. Площадь квадрата можно найти, умножив длину его стороны на эту же длину. Таким образом, если известна площадь квадрата, можно найти длину его стороны.
Расчеты для нахождения стороны квадрата при заданной площади довольно просты: нужно извлечь корень из значения площади. В нашем случае, когда площадь квадрата равна 36, мы можем найти длину его стороны, извлекая квадратный корень из значения 36.
Корень из 36 равен 6. Итак, сторона квадрата при площади 36 равна 6. Это значит, что все 4 стороны квадрата имеют длину 6.
Как определить длину стороны квадрата при известной площади 36 квадратных единиц?
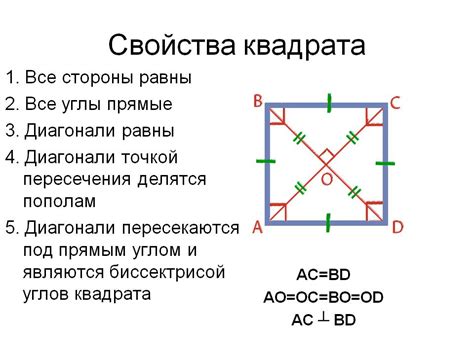
В данном случае, известно что площадь квадрата равна 36 квадратных единиц. Подставим данное значение в формулу и найдем длину стороны:
36 = a^2
Для решения данного уравнения возьмем квадратный корень от обеих сторон:
√36 = √a^2
Упростим выражение:
6 = a
Таким образом, длина стороны квадрата при известной площади 36 квадратных единиц равна 6 единицам.
Формула для вычисления стороны квадрата по его площади
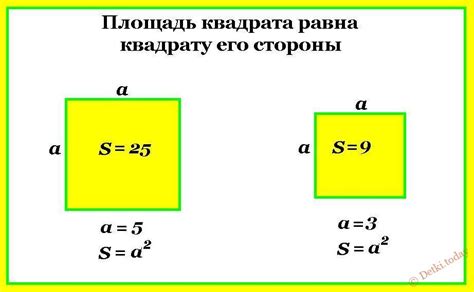
Существует формула, которая позволяет вычислить сторону квадрата по его площади. Для этого необходимо найти квадратный корень из площади. Таким образом формула выглядит следующим образом:
| Площадь квадрата: | 36 |
| Сторона квадрата: | 6 |
В данной формуле сначала находим квадратный корень из площади, а затем округляем полученное значение до ближайшего целого числа. В данном случае, когда площадь квадрата равна 36, сторона квадрата будет равна 6.
Таким образом, формула для вычисления стороны квадрата по его площади является квадратный корень из площади.
Как вычислить корень квадратный из числа

Методы вычисления корня квадратного:
1. Геометрический метод: построение квадрата со стороной, равной исходному числу, и нахождение длины стороны нового квадрата, равной корню квадратному.
2. Метод последовательных приближений: нахождение приближенного значения корня квадратного путем итеративного вычисления значения исходного числа.
3. Метод Ньютона: применение итерационной формулы, основанной на аппроксимации функции и ее производной.
Результатом вычисления корня квадратного из числа будет число, равное положительному значению корня. Чтобы найти отрицательное значение, нужно умножить результат на -1.
Важно помнить, что вычисление корня квадратного из числа может привести к бесконечной десятичной дроби, поэтому для практических целей обычно используют приближенные значения.
Пример вычисления длины стороны квадрата
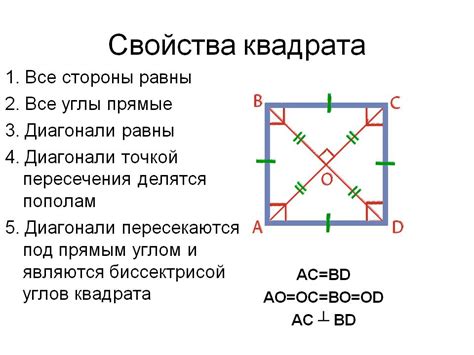
Для вычисления длины стороны квадрата, когда известна его площадь, нужно применить следующую формулу:
Сторона = √(Площадь квадрата)
Таким образом, для нахождения стороны квадрата при площади 36, нужно взять квадратный корень из 36. Квадратный корень из 36 равен 6.
Следовательно, сторона квадрата при площади 36 равна 6.



