Как вычислить значение синуса для дробного числа — простые способы и формулы

Синус - это одна из основных тригонометрических функций, которая выражает отношение противолежащего катета к гипотенузе в прямоугольном треугольнике. Обычно синус определяется для углов, которые являются действительными числами. Однако, иногда может возникнуть необходимость вычислить синус для дробных чисел, например, для аргументов, которые представляют собой результат математических выражений или расчетов.

Нахождение синуса дробного числа может быть решено с использованием различных методов и приемов. Один из таких методов - разложение в ряд Тейлора. Этот метод основан на приближенном представлении функции через сумму бесконечного ряда слагаемых. Чем больше слагаемых в ряду, тем более точное приближение получается. Однако, при использовании этого метода необходимо учитывать, что для дробных чисел результат может быть менее точным из-за ограниченного числа используемых слагаемых.

Другим методом нахождения синуса дробного числа является интерполяция. В этом методе значения синуса для целых чисел берутся из заранее подготовленной таблицы, а затем осуществляется линейная интерполяция между ближайшими значениями в таблице. Этот метод позволяет получить более точное значение синуса для дробных аргументов, однако требует заранее подготовленной таблицы значений и дополнительных вычислительных операций.

Выбор метода для нахождения синуса дробного числа зависит от требуемой точности, доступных вычислительных ресурсов и времени. Оптимальный метод может различаться в зависимости от конкретной задачи и параметров. Величина ошибки приближенного значения синуса для дробного числа также должна быть учтена и проанализирована.

Методы нахождения синуса дробного числа

Нахождение синуса дробного числа может быть выполнено с использованием различных методов и приемов. В данной статье рассмотрим несколько из них.

1. Ряд Тейлора

Один из наиболее распространенных методов нахождения синуса дробного числа - использование ряда Тейлора. В основе этого метода лежит разложение синуса в бесконечную сумму:

sin(x) = x - x^3/3! + x^5/5! - x^7/7! + ...

Данный ряд сходится для всех значений x и позволяет находить синус с заданной точностью.

2. Интерполяционный метод

Другой распространенный метод - интерполяционный метод. Он основан на аппроксимации синуса дробного числа с использованием значения синуса уже известного близкого значения. Данный метод позволяет достичь высокой точности вычислений.

3. Геометрический метод

Еще один метод нахождения синуса дробного числа - геометрический метод. Он основывается на геометрической интерпретации синуса и использовании соответствующих геометрических фигур и формул.

Выбор метода нахождения синуса дробного числа зависит от требуемой точности вычислений, доступных вычислительных ресурсов и специфики задачи.

Метод тейлоровского разложения

Принцип работы метода заключается в следующем:

1. Выбирается центр разложения, который может быть любым числом.
2. Функция синуса разлагается в ряд Тейлора в окрестности выбранного центра.
3. Ряд Тейлора содержит бесконечную сумму слагаемых, каждое из которых представляет собой производную функции синуса в точке разложения, умноженную на степень отклонения от центра.
4. Ряд Тейлора обрезается до конечного числа слагаемых, что позволяет получить приближенное значение синуса дробного числа.

Чем больше слагаемых участвует в разложении, тем точнее будет полученное приближение. Однако, для практического использования обычно достаточно использовать несколько первых слагаемых.

Метод тейлоровского разложения применяется во многих областях математики и физики, где требуется вычисление сложных функций при малых значениях аргумента. Он также широко используется в программировании и научных вычислениях.

Метод интерполяции

Идея метода заключается в том, чтобы представить синус в виде многочлена, который проходит через некоторые заданные точки. Затем, используя полином Лагранжа, искомое значение синуса может быть вычислено через вычисление значения многочлена в данной точке.

Для использования метода интерполяции необходимо задать набор узловых точек, через которые должен проходить интерполяционный многочлен. Чем больше точек, тем более точная аппроксимация может быть получена. Однако, при увеличении количества точек возрастает и сложность вычислений.

Метод интерполяции является одним из классических методов приближенного нахождения синуса дробного числа. Он позволяет достичь достаточной точности вычислений при относительно небольшом количестве узловых точек.

Метод численного интегрирования

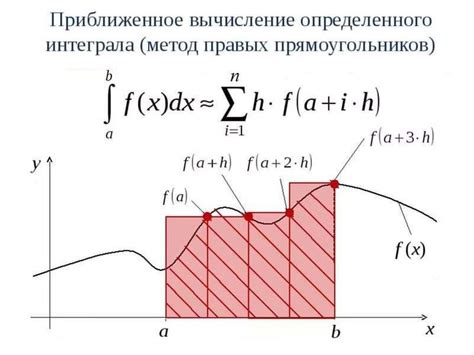
Метод численного интегрирования используется для приближенного нахождения значения определенного интеграла. Этот метод основывается на аппроксимации интеграла с помощью суммы значений функции на некотором множестве точек из заданного интервала.

Существует несколько основных методов численного интегрирования, включая метод прямоугольников, метод тrapezoid, метод Симпсона и другие. Каждый из этих методов имеет свои особенности и применяется в разных ситуациях.

Метод прямоугольников заключается в разбиении интервала на равные отрезки и аппроксимации значения интеграла с помощью суммы высот треугольников, образованных на этих отрезках.

Метод тrapezoid основан на приближении интеграла с помощью трапеций, образованных на интервале.

Метод Симпсона использует квадратичные функции для приближения значения интеграла. Этот метод обладает более высокой точностью, чем метод прямоугольников и метод trapezoid.

Выбор метода численного интегрирования зависит от конкретной задачи и требуемой точности результата. При решении задачи по вычислению синуса дробного числа, к численному интегрированию можно применить указанные методы и получить приближенное значение синуса.

Метод рациональной аппроксимации

Для начала необходимо рассмотреть разложение синуса в ряд Тейлора:

sin(x) = x - (x^3)/3! + (x^5)/5! - (x^7)/7! + ...

Возможно представление синуса дробного числа в виде суммы рациональных функций. Для этого используется аппроксимация тригонометрических функций при помощи рациональных дробей.

Процесс аппроксимации начинается с выбора рациональной функции, которая имеет вид:

f(x) = (P(x))/(Q(x)),

где P(x) и Q(x) – многочлены, ищущиеся в виде:

P(x) = a0 + a1*x + a2*x^2 + ... + an*x^n,

Q(x) = b0 + b1*x + b2*x^2 + ... + bm*x^m.

Коэффициенты a0, a1, ..., an, b0, b1, ..., bm подбираются таким образом, чтобы рациональная функция как можно лучше аппроксимировала синус дробного числа.

После определения многочленов P(x) и Q(x), коэффициенты a0, a1, ..., an, b0, b1, ..., bm находятся при помощи различных методов, таких как интерполяция, метод Ньютона или метод наименьших квадратов.

Полученная рациональная функция f(x) затем может быть использована для нахождения аппроксимированного значения синуса дробного числа.

Метод рациональной аппроксимации имеет свои преимущества и недостатки. Он может быть эффективен для достижения высокой точности при нахождении синуса дробных чисел, особенно при использовании специализированных алгоритмов и библиотек.

Однако стоит учитывать, что метод рациональной аппроксимации может быть сложным в реализации и требовать большого количества вычислительных ресурсов. Также необходимо учитывать потенциальные ограничения при использовании рациональной функции для аппроксимации синуса дробного числа в некоторых пределах.

В целом, метод рациональной аппроксимации является важным инструментом для нахождения синуса дробного числа с высокой точностью и может быть полезным в различных областях науки и техники, где требуется точный расчет значений синуса.

Метод приведения к стандартному диапазону

Для начала необходимо привести заданное дробное число к стандартному диапазону от 0 до 2π. Для этого число необходимо разделить на 2π и сохранить только дробную часть результата. Таким образом, мы получим число в интервале от 0 до 1.

Затем необходимо перемножить полученное число на 2π, чтобы вернуться к исходному диапазону.

Используя этот метод, можно вычислять синус дробного числа с высокой точностью и эффективностью. При этом не требуется вычислять синус для большого диапазона значений, а пределы вычислений ограничены установленным интервалом от 0 до 2π.

Этот метод особенно полезен при работе с компьютерными алгоритмами, где требуется быстрое и точное вычисление синуса дробного числа. Он позволяет снизить вычислительную сложность и упростить реализацию программного кода.

Метод приближенного вычисления

Согласно ряду Тейлора, синус x может быть записан как бесконечная сумма слагаемых. Каждое слагаемое зависит от степени x. Чем больше слагаемых учитывается в ряду, тем точнее будет значение синуса. Однако для дробных чисел необходимо учитывать большое количество слагаемых, что может сильно замедлить вычисления.

Метод приближенного вычисления синуса дробного числа заключается в том, чтобы сократить количество учитываемых слагаемых, не затрачивая при этом слишком много вычислительных ресурсов. Упрощенный алгоритм может быть реализован с использованием лишь нескольких первых слагаемых ряда Тейлора.

При вычислении синуса дробного числа можно также использовать методы интерполяции, при которых значения синуса для некоторых дискретных значений аргумента заранее вычисляются и сохраняются в таблице. Затем для вычисления синуса дробного числа применяется метод интерполяции, позволяющий находить значения синуса между уже известными значениями. Это позволяет существенно ускорить вычисления и получить достаточно точные значения синуса.

Метод определения приближенной периодичности

Для нахождения синуса дробного числа может быть использован метод определения приближенной периодичности. Этот метод заключается в анализе значений синуса для различных значений аргумента и поиске периодических закономерностей.

Для определения приближенной периодичности можно использовать таблицу значений синуса для различных значений аргумента. Для этого нужно выбрать несколько дробных значений аргумента, например, таких как π/4, π/2, 3π/4 и т.д., и вычислить значения синуса для этих аргументов. Затем нужно проанализировать полученные значения и найти периодические закономерности.

Определение приближенной периодичности может быть полезным при расчете синуса дробных значений аргумента, так как позволяет использовать периодические закономерности для более точного вычисления значений синуса.

Метод матричной аппроксимации

Данный метод позволяет достичь высокой точности вычисления синуса дробного числа, особенно при больших значениях аргумента. Его основной принцип заключается в использовании матриц для упрощения вычислений и сокращения количества операций.

Для начала необходимо привести дробное число к диапазону от 0 до 1, используя свойство периодичности синуса. Затем разложить синус в ряд Тейлора с заданной точностью, например, до n-го члена.

После этого можно приступить к матричной аппроксимации. Для этого необходимо создать специальную матрицу размером (2n+1) x (2n+1), где n - количество членов в разложении Тейлора. Каждый элемент матрицы будет представлять собой значение k-го члена разложения, умноженное на (2n+1 - k-й элемент вектора аппроксимации).

Далее необходимо сложить все элементы матрицы и получить конечную аппроксимацию синуса дробного числа. Результат будет представлять собой значение синуса с заданной точностью.