Площадь параллелограмма - это одно из важных понятий геометрии, которое применяется при решении простейших и сложных задач. Найти площадь параллелограмма можно различными способами, но основой является единственная формула, которая позволяет рассчитать этот параметр.
Основной принцип доказательства формулы площади параллелограмма - базируется на теореме о площади треугольника: площадь треугольника равна половине произведения длины основания на высоту, опущенную на это основание. Из этой теоремы мы можем вывести формулу площади параллелограмма.
Для этого достаточно разбить параллелограмм на два треугольника, проведя диагональ параллелограмма. Таким образом, получим два треугольника, каждый из которых можно рассчитать по формуле площади треугольника. После этого просто сложим полученные значения площадей треугольников, и мы получим площадь всего параллелограмма.
Что такое площадь параллелограмма?

Для описания площади параллелограмма используется формула, основанная на вычислении площади треугольника. Суть формулы заключается в нахождении высоты параллелограмма и умножении ее на одну из сторон.
Если обозначить основание параллелограмма как a, а высоту как h, то площадь можно выразить следующей формулой:
Площадь = a * h
Здесь a представляет собой любую сторону параллелограмма, а h - расстояние между параллельными сторонами, перпендикулярное к основанию.
Значение площади параллелограмма измеряется в квадратных единицах, таких как квадратные единицы длины, например, квадратные метры или квадратные сантиметры.
Определение и основные понятия

Стороны параллелограмма - это отрезки, соединяющие вершины параллелограмма. Они обозначаются буквами a, b, c и d.
Углы параллелограмма - это углы, образованные пересечением сторон. Обозначаются буквами A, B, C и D.
Диагонали параллелограмма - это отрезки, соединяющие вершины, не являющиеся соседними. В параллелограмме есть две диагонали: AC и BD.
Прямоугольный параллелограмм и его площадь

Формула для вычисления площади прямоугольного параллелограмма очень простая - площадь равна произведению длины одной из сторон на высоту, опущенную на эту сторону.
Для наглядности, можно представить прямоугольный параллелограмм в виде таблицы:
| Сторона | Высота | Площадь |
|---|---|---|
| a | h | S = a * h |
Где a - длина одной из сторон параллелограмма, h - высота, опущенная на эту сторону, S - площадь.
Например, если у нас есть прямоугольный параллелограмм со стороной a равной 5 и высотой h равной 3, то его площадь будет:
| Сторона | Высота | Площадь |
|---|---|---|
| 5 | 3 | S = 5 * 3 = 15 |
Таким образом, площадь данного прямоугольного параллелограмма равна 15.
Наклонный параллелограмм и его площадь
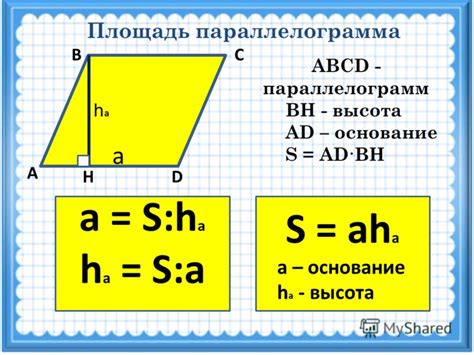
Для вычисления площади наклонного параллелограмма можно воспользоваться формулой:
| Площадь | = | Основание | * | Высота |
| = | AB | * | h |
где AB – основание параллелограмма, а h – высота параллелограмма, проведенная на основание.
Величину основания AB можно получить, измерив длину любой из его сторон. Высоту h можно определить, измерив расстояние между противоположными сторонами параллелограмма.
Таким образом, для вычисления площади наклонного параллелограмма нужно знать и основание, и высоту. Значение площади будет выражено в квадратных единицах.
Формула для вычисления площади параллелограмма
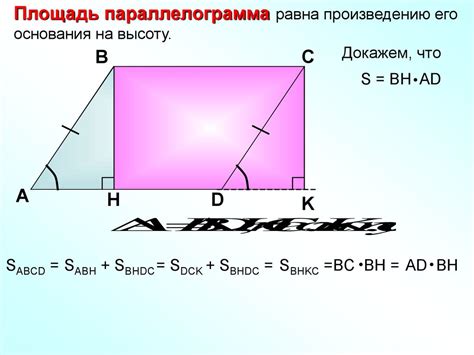
Площадь параллелограмма можно вычислить, зная длины одной стороны и высоту, опущенную на эту сторону.
Пусть a - длина стороны параллелограмма, h - высота, опущенная на эту сторону. Тогда площадь S параллелограмма равна:
S = a * h
Таким образом, чтобы найти площадь параллелограмма, нужно умножить длину одной из его сторон на высоту, опущенную на эту сторону.
Эта формула основана на том, что параллелограмм можно разбить на два треугольника, у которых одна из сторон - это сторона параллелограмма, а другая - высота. Площадь треугольника равна половине произведения длины основания на высоту. Поскольку в параллелограмме два таких треугольника, площадь параллелограмма можно найти, умножив площадь одного из треугольников на 2.
Формула для вычисления площади параллелограмма является основой для решения задач, связанных с нахождением площадей геометрических фигур.
Доказательство формулы для площади параллелограмма
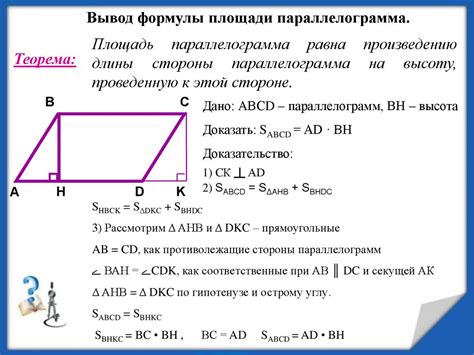
Для доказательства формулы для площади параллелограмма мы воспользуемся свойствами векторов и понятием векторного произведения.
Пусть у нас есть параллелограмм с основанием, обозначенным векторами a и b, а высота параллелограмма, проведенная к основанию, обозначена вектором h.
Векторное произведение векторов a и b можно выразить следующей формулой:
a × b = |a| * |b| * sin(θ) * n,
где |a| и |b| - длины векторов a и b, θ - угол между a и b, а n - единичный вектор, перпендикулярный плоскости, образованной векторами a и b.
Вектор h является высотой параллелограмма и перпендикулярен к основанию, поэтому он также перпендикулярен к вектору a. То есть, вектор h перпендикулярен к плоскости, образованной векторами a и b.
Таким образом, векторное произведение векторов a и h будет равно нулю:
a × h = 0.
Из этого следует, что скалярное произведение векторов a и h также будет равно нулю:
a · h = 0.
Но скалярное произведение векторов a и h можно представить в виде:
a · h = |a| * |h| * cos(θ),
где |h| - длина вектора h.
Так как скалярное произведение равно нулю, получаем:
|a| * |h| * cos(θ) = 0.
Из этого уравнения следует, что либо длина вектора a равна нулю (что является невозможным), либо длина вектора h равна нулю.
Таким образом, длина вектора h равна нулю, что означает, что площадь параллелограмма равна нулю.
Таким образом, мы доказали формулу для площади параллелограмма:
Площадь = |a| * |b| * sin(θ).



