Геометрия включает в себя множество интересных тем и концепций, одной из которых является доказательство равенства треугольников. Доказывать равенство треугольников может быть не только интересно, но и полезно, особенно при решении геометрических задач.
Основное правило для доказательства равенства треугольников - это правило равных сторон и равных углов. Если у двух треугольников все стороны равны друг другу, а также все углы равны, то эти треугольники считаются равными. Доказывая равенство треугольников, мы можем использовать различные методы, такие как сравнение сторон, равенство углов или использование свойств равных треугольников.
Один из способов доказать равенство треугольников - это построение треугольников с помощью отрезков и равенства сторон или углов. Используя конструкции с помощью циркуля и линейки, мы можем создать два треугольника с равными сторонами и углами. Этот метод позволяет визуально увидеть, что два треугольника являются равными и можно утверждать их равенство.
Равенство треугольников:
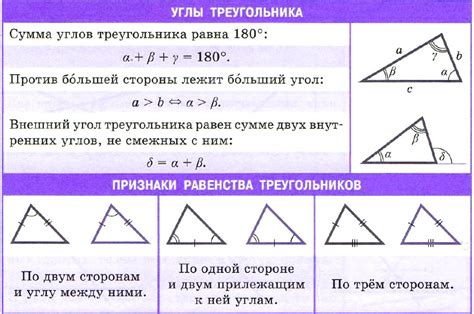
Для доказательства равенства двух треугольников достаточно установить, что соответствующие их стороны и углы равны. То есть, если каждая сторона и каждый угол одного треугольника равны соответственно каждой стороне и каждому углу другого треугольника, то эти треугольники считаются равными.
Равенство треугольников можно доказать с помощью различных методов и теорем, таких как равенство по стороне-уголу-стороне (СУС), сторона-сторона-сторона (ССС), угол-сторона-угол (УСУ) и другие.
Это понятие имеет большое значение в геометрии, так как позволяет устанавливать соответствия и связи между различными треугольниками и использовать эти свойства при решении задач и построении фигур.
Методы доказательства равенства треугольников:
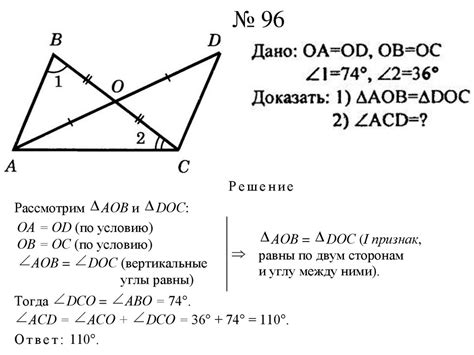
1. Метод равных сторон:
Если два треугольника имеют все стороны равными, то они равны.
2. Метод равных углов:
Если два треугольника имеют все углы равными, то они равны.
3. Метод сторона-угол-сторона (СУС):
Если два треугольника имеют соответственно равные стороны, равный угол и равные стороны, то они равны.
4. Метод угол-сторона-угол (УСУ):
Если два треугольника имеют соответственно равные углы, равную сторону и равные углы, то они равны.
5. Метод сторона-сторона-сторона (ССС):
Если два треугольника имеют соответственно равные стороны, то они равны.
6. Метод угол-угол-сторона (УУС):
Если два треугольника имеют соответственно равные углы, равные углы и равную сторону, то они равны.
Использование этих методов позволяет доказывать равенство треугольников с помощью геометрических свойств и правил.



