Как убедительно доказать перпендикулярность двух прямых а и б — эффективные способы и методы

Перпендикулярные прямые - основное понятие геометрии, о котором знает каждый школьник. Но как доказать перпендикулярность двух данных прямых? В этой статье мы рассмотрим несколько уроков и примеров, которые помогут вам разобраться в этом вопросе.

Перпендикулярность - это свойство двух прямых, означающее, что они образуют прямой угол, то есть угол равен 90 градусам. Для доказательства перпендикулярности необходимо предъявить достаточно сильные аргументы и использовать соответствующие геометрические методы. Рассмотрим несколько простых уроков и примеров, которые помогут вам в этом.

В первом уроке мы рассмотрим метод, основанный на применении свойств параллельных прямых и одного из базовых свойств перпендикулярных прямых. Во-первых, мы можем использовать свойство параллельных прямых, согласно которому две параллельные прямые пересекаются под прямым углом со своими положительными наклонами. Во-вторых, мы можем использовать базовое свойство перпендикулярных прямых - угол между перпендикулярными прямыми всегда будет равен 90 градусам.

Определение перпендикулярности

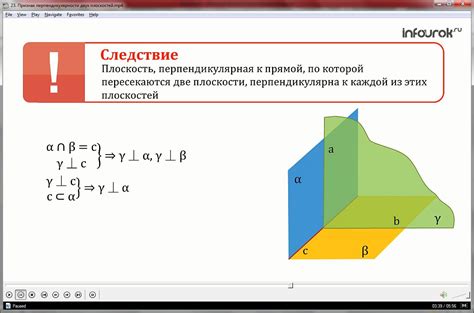
Перпендикулярными называют прямые, которые пересекаются под прямым углом. Для проверки перпендикулярности двух прямых а и б необходимо выполнить следующие действия:

1. Найдите уравнения двух прямых а и б в виде y = k₁x + b₁ и y = k₂x + b₂, где k₁ и k₂ - коэффициенты наклона, а b₁ и b₂ - свободные члены.

2. Установите, равны ли коэффициенты наклона k₁ и k₂. Если они равны, прямые а и б параллельны, а не перпендикулярны. Если коэффициенты наклона различаются, приступайте к следующему шагу.

3. Вычислите произведение k₁ * k₂. Если произведение равно -1, то прямые а и б перпендикулярны. В противном случае, они не являются перпендикулярными.

Выполнив эти шаги, вы сможете определить, перпендикулярны ли две заданные прямые а и б в данной системе координат.

Что такое перпендикулярные прямые?

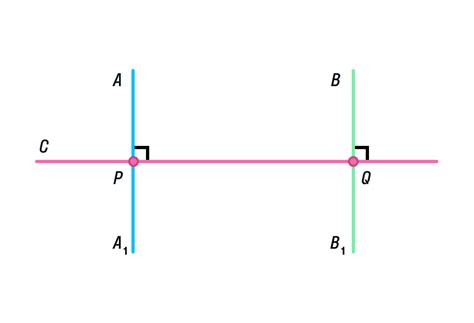
Для понимания понятия перпендикулярности прямых, важно знать, что прямые линии обращены в бесконечность и не имеют начала или конца. Когда две прямые пересекаются под прямым углом, они образуют четыре прямых угла, каждый из которых равен 90 градусов.

Перпендикулярные прямые очень важны в геометрии и на практике. Они используются для построения косметических квадратов и прямоугольников, а также для нахождения направления движения объектов на плоскости. В архитектуре, инженерии и других отраслях они служат основой для построения и измерения прямых линий.

Чтобы доказать, что две прямые являются перпендикулярными, можно использовать специальную аксиому или геометрические свойства. Например, если две прямые имеют одну общую точку и все углы, образованные этими прямыми, равны 90 градусов, то они являются перпендикулярными.

Критерии перпендикулярности

Для доказательства перпендикулярности двух прямых 'а' и 'б' существуют несколько критериев:

1. Критерий, основанный на наклонных углах. Если угол между прямыми равен 90 градусам, то они перпендикулярны друг другу.

2. Критерий, основанный на градиентах прямых. Если произведение градиентов прямых равно -1 (градиент одной прямой равен обратному числу, противоположному знаку градиента другой прямой), то прямые перпендикулярны.

3. Критерий, основанный на коэффициентах наклона. Если произведение коэффициентов наклона прямых равно -1/90 (как соотношение градусов в радианы), то прямые перпендикулярны друг другу.

Учет этих критериев позволяет легко проверить и доказать перпендикулярность двух прямых на плоскости.

Первый критерий

Второй критерий

Второй критерий перпендикулярности двух прямых а и б устанавливает, что если уравнения прямых удовлетворяют условию a1 * b2 + a2 * b1 = 0, то прямые перпендикулярны друг другу.

Для доказательства данного критерия нужно иметь уравнения двух прямых в виде:

При этом a1, a2 - коэффициенты наклона прямых, b1, b2 - коэффициенты свободного члена.

Применяя второй критерий, мы можем убедиться, что две прямые являются перпендикулярными:

a1 * b2 + a2 * b1 = (a1 * a2) * x + (a1 * b2 + a2 * b1) = a1 * b2 + a2 * b1 = 0

Следовательно, если данное равенство выполнено, то это является доказательством перпендикулярности двух прямых а и б.

Доказательства перпендикулярности

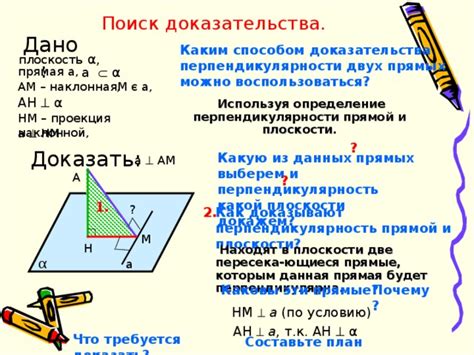
Перпендикулярность двух прямых может быть доказана различными способами. Рассмотрим некоторые из них:

1. Углы между прямыми. Если угол между двумя прямыми равен 90 градусам, то они являются перпендикулярными. Для доказательства этого факта можно использовать геометрические свойства углов: если две прямые пересекаются и угол между ними равен 90 градусам, то они перпендикулярны.

2. Коэффициенты наклона прямых. Для двух прямых, перпендикулярных друг другу, произведение их коэффициентов наклона равно -1. Если угол между двумя прямыми равен 90 градусам, то их коэффициенты наклона будут взаимно обратными числами.

3. Векторная алгебра. Если вектор, параллельный одной из прямых, перпендикулярен вектору, параллельному другой прямой, то прямые также перпендикулярны. Для доказательства перпендикулярности прямых можно использовать свойства операций над векторами, такие как скалярное произведение и векторное произведение.

4. Теорема Пифагора. Если треугольник, образованный двумя прямыми и отрезком, соединяющим их точки пересечения, является прямоугольным, то прямые перпендикулярны. Для доказательства перпендикулярности можно использовать теорему Пифагора, которая устанавливает связь между длинами сторон прямоугольного треугольника.

Использование этих и других методов позволяет доказать перпендикулярность двух прямых и установить взаимоотношение между ними.

Двумя перпендикулярными прямыми

Для доказательства перпендикулярности двух прямых a и b необходимо убедиться, что угол между ними равен 90 градусам. Существует несколько способов доказательства перпендикулярности:

1. Использование свойств перпендикулярных прямых. Если известно, что прямые a и b проходят через одну точку и перпендикулярны друг другу, то можно воспользоваться свойствами перпендикулярных прямых для доказательства их перпендикулярности.
2. Использование геометрических построений. Можно построить перпендикуляр к одной из прямых и проверить, пересекает ли он вторую прямую под прямым углом. Если это так, то прямые a и b перпендикулярны.

Все эти методы позволяют доказать перпендикулярность двух прямых a и b и являются основой для решения задач, связанных с перпендикулярными прямыми в геометрии.