Углы в треугольнике являются одним из основных элементов геометрии, и их расчет является неотъемлемой частью многих задач. В частности, косинус угла a в треугольнике имеет важное значение при решении различных задач на нахождение сторон и площадей треугольников. Косинус угла a определяет отношение длины стороны прилежащей к данному углу к длине гипотенузы.
Для расчета косинуса угла a в прямоугольном треугольнике можно использовать простую математическую формулу: cos(a) = прилежащая сторона / гипотенуза. Эта формула основана на определении косинуса через отношение катета и гипотенузы.
Для расчета косинуса угла a в общем случае треугольника можно воспользоваться более общей формулой: cos(a) = (b^2 + c^2 - a^2) / (2 * b * c), где a, b, c - стороны треугольника, противолежащие углу a. Эта формула основана на теореме косинусов, которая позволяет находить косинус угла в произвольном треугольнике.
Расчет косинуса угла a может быть полезен в различных сферах, например, при решении задач по планиметрии, геодезии или физике. Познание методов расчета косинуса позволяет более глубоко понять геометрию треугольников и применять ее в решении различных практических задач.
Определение косинуса угла а
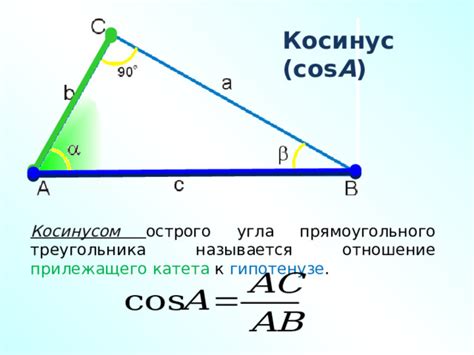
Для определения косинуса угла а с помощью формулы необходимо знать значения сторон треугольника.
- Прямоугольный треугольник ABC.
- Угол а в треугольнике ABC.
- Длины сторон треугольника: AB, BC и AC.
Формула для расчета косинуса угла а:
cos(a) = AB / AC
Данную формулу можно использовать для определения значения косинуса угла а, если известны значения сторон треугольника и угол а.
Косинус угла а может принимать значения от -1 до 1, где значению -1 соответствует угол 180 градусов, а значению 1 - угол 0 градусов.
Зная значение косинуса угла а, можно использовать его для решения различных задач, связанных с геометрией и физикой.
Основные понятия и формулы

cos(α) = adjacent/hypotenuse
где adjacent – длина прилежащего катета, а hypotenuse – длина гипотенузы.
Косинус угла α имеет значения от -1 до 1. Если угол α равен 0°, то косинус равен 1. Если угол α равен 90°, то косинус равен 0. Если угол α равен 180°, то косинус равен -1.
Косинус угла α в треугольнике также может быть выражен через расстояния между точками на плоскости. Если имеются точки A(x1, y1) и B(x2, y2), то косинус угла α между векторами AB и OA (где O(0, 0) – начало координат) можно вычислить по формуле:
cos(α) = [(x1 - x2) * x1 + (y1 - y2) * y1] / [√((x1 - x2)^2 + (y1 - y2)^2) * √(x1^2 + y1^2)]
где x1, y1 – координаты точки A, x2, y2 – координаты точки B.
Методы расчета косинуса угла α

- Геометрический метод: Для расчета косинуса угла α можно использовать геометрический метод. Для этого строится прямоугольный треугольник, в котором известны длины прилежащего катета и гипотенузы. Затем используется соотношение косинуса: cos α = a / c, где а - длина прилежащего катета и с - длина гипотенузы.
- Тригонометрический метод: Для расчета косинуса угла α можно использовать тригонометрический метод. Для этого необходимо знать значения соответствующих тригонометрических функций для угла α. Косинус угла α равен отношению длины прилежащего катета к гипотенузе, т.е. cos α = a / c.
- Использование табличных данных: В табличных данных для тригонометрических функций можно найти значения косинуса углов α. По известному значению угла α в таблице можно найти соответствующее значение косинуса угла α.
Все эти методы позволяют расчитать косинус угла α в прямоугольных треугольниках и помогают в решении различных задач, связанных с геометрией и тригонометрией.
Геометрический метод

Геометрический метод расчета косинуса угла а может быть использован для определения длин сторон треугольника и его углов на основе известных данных. Для этого необходимо использовать свойства треугольника и геометрические конструкции.
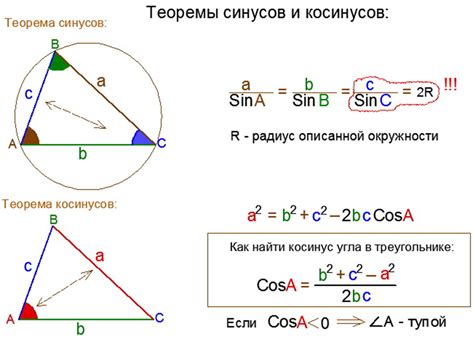
Один из основных способов расчета косинуса угла а заключается в использовании теоремы косинусов. Согласно этой теореме, квадрат длины стороны треугольника равен сумме квадратов длин двух других сторон минус двойное произведение этих сторон на косинус угла между ними. Таким образом, формула для расчета косинуса угла а выглядит следующим образом:
cos a = (b^2 + c^2 - a^2) / (2 * b * c)
Геометрический метод позволяет удобно определять значения углов треугольника на основе известных длин его сторон. Также с его помощью можно определить длины сторон треугольника, если известны углы и одна из сторон.
Применив геометрический метод расчета косинуса угла а, можно получить точное значение этого тригонометрического параметра и использовать его для решения различных задач из области геометрии и тригонометрии.
Тригонометрические формулы

В математике существуют различные тригонометрические формулы, которые позволяют вычислять различные значения и свойства тригонометрических функций. Рассмотрим некоторые из них:
1. Формулы сложения и вычитания аргументов:
sin(a ± b) = sin a * cos b ± cos a * sin b
cos(a ± b) = cos a * cos b ∓ sin a * sin b
tan(a ± b) = (tan a ± tan b) / (1 ∓ tan a * tan b)
2. Формулы двойного угла:
sin(2a) = 2 * sin a * cos a
cos(2a) = cos² a - sin² a
tan(2a) = 2 * tan a / (1 - tan² a)
3. Формула понижения степени:
sin² a = (1 - cos 2a) / 2
cos² a = (1 + cos 2a) / 2
tan² a = (1 - cos 2a) / (1 + cos 2q)
Эти формулы позволяют связывать значения тригонометрических функций при различных углах и проводить различные тригонометрические преобразования. Знание этих формул является важным для решения множества задач в различных областях науки и техники.
Применение косинуса угла а в треугольнике
Косинус угла а в треугольнике имеет широкое применение в геометрии и физике. С его помощью можно вычислять различные параметры треугольника и решать задачи, связанные с его конструкцией и свойствами.
Одним из основных применений косинуса угла а является вычисление длины стороны треугольника. Используя формулу косинуса, можно найти длину стороны, зная длины двух других сторон и величину противолежащего угла. Это позволяет решать задачи на построение треугольников и нахождение неизвестных сторон.
Также косинус угла а используется для нахождения площади треугольника. При известных длинах двух сторон и величине между ними угла, можно вычислить площадь треугольника, используя формулу площади треугольника через полупериметр.
Другим важным применением косинуса угла а является нахождение высоты треугольника. Высота - это перпендикуляр, опущенный из вершины треугольника на противоположную сторону. Используя формулу косинуса, можно вычислить длину высоты, зная длины двух сторон и угол между ними.
Косинус угла а также применяется в задачах на нахождение площади параллелограмма и ромба. Параллелограмм является особой формой четырехугольника, у которого противолежащие стороны параллельны. Используя формулу косинуса, можно вычислить площадь параллелограмма по длинам его сторон и углу между ними.
Ромб - это четырехугольник, у которого все стороны равны. Используя косинус угла а, можно вычислить площадь ромба, зная длины его сторон.
Все эти применения косинуса угла а делают его важным инструментом для решения задач в геометрии и физике. Используя эту формулу, можно находить неизвестные стороны и углы треугольника, а также вычислять площадь различных фигур.



