Как понять, что такое степень по алгебре в 7 классе и как с ней работать

Степень – это основное понятие алгебры, которое знакомят учеников уже в седьмом классе. Степень является мощным инструментом для упрощения математических выражений и решения уравнений. В данной статье мы рассмотрим, что такое степень, какие правила ее используют и как применять их в практике.

Степень – это обозначение для того, чтобы упростить запись чисел и алгебраических выражений. Число или выражение, возведенное в степень, представляет собой произведение данного числа или выражения на себе самое определенное количество раз.

Степень имеет две части: основание (число или выражение) и показатель (натуральное число, выражение или величина). Основание возведено в степень, определяемую показателем.

Определение степени

Степень числа обозначается с помощью числа, называемого основанием, и числа, называемого показателем степени. Основание - это число, которое умножается само на себя несколько раз, а показатель степени - это количество раз, сколько умножается основание.

Например, число 2 в степени 3 (2³) означает, что число 2 умножается на себя три раза: 2 * 2 * 2 = 8.

Степень может быть выражена с помощью записи в виде индекса. Например, 2³ можно записать в виде числа 2 с нижним индексом 3.

Степени можно обозначать и отрицательными числами. Например, 2^-2 означает, что число 2 возводится в степень -2 и является обратным значением 2².

Степень положительного числа

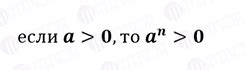
Степень положительного числа выражается с помощью символа '^', где показатель указывается справа от основания. Например, 3^2 означает, что число 3 возводится во вторую степень.

Возведение числа в степень позволяет получить результат, который является произведением данного числа на себя нужное количество раз.

Например, если мы возведем число 2 в степень 3, то получим:

• 2^3 = 2 × 2 × 2 = 8

При возведении положительного числа в степень возможны следующие случаи:

1. Если показатель степени равен 0, то результат равен 1: a^0 = 1.
2. Если показатель степени равен 1, то результат равен самому числу: a^1 = a.
3. Если показатель степени больше 1, то результат равен произведению числа на себя указанное количество раз: a^m = a × a × ... × a (m раз).

Вычисление степени положительного числа осуществляется путем умножения числа на себя указанное количество раз. Например, чтобы вычислить результат 3^4, нужно умножить число 3 на себя 4 раза:

• 3^4 = 3 × 3 × 3 × 3 = 81

Таким образом, зная правила возведения числа в степень, можно вычислять результаты различных математических задач и заданий, связанных со степенями положительных чисел.

Степень отрицательного числа

Для нахождения степени отрицательного числа сначала нужно проверить, является ли показатель степени четным или нечетным числом. Если показатель степени четный, то результат будет положительным числом. Если показатель степени нечетный, то результат будет отрицательным числом.

Например, если у нас есть отрицательное число -2 и показатель степени равен 3, то мы должны умножить -2 на себя 3 раза:

-2 × -2 × -2 = -8

Получаем результат -8, который является отрицательным числом, так как показатель степени нечетный.

Если показатель степени равен 0, то результат всегда будет равен 1, так как любое число, возведенное в степень 0, равно 1.

Таким образом, степень отрицательного числа определяется показателем степени и может быть как положительным, так и отрицательным числом, а также нулем в случае, если показатель степени равен 0.

Свойства степеней

Основные свойства степеней:

• Свойство 1: Произведение степеней с одинаковыми основаниями равно степени с тем же основанием и суммой показателей. То есть, аⁿ * а^m = а^n+m.
• Свойство 2: Частное степеней с одинаковыми основаниями равно степени с тем же основанием и разностью показателей. То есть, аⁿ / а^m = а^n-m.
• Свойство 3: Степень степени равна степени с тем же основанием и произведением показателей. То есть, (аⁿ)^m = а^n*m.
• Свойство 4: Степень числа 1 равна 1. То есть, 1ⁿ = 1.
• Свойство 5: Степень числа 0, кроме 0⁰, равна 0. То есть, 0ⁿ = 0 (при n ≠ 0).

Свойства степеней помогают упростить расчеты и выполнять операции с числами в степени более эффективно и удобно.

Примеры задач по степеням

Разберем несколько примеров задач, чтобы лучше разобраться с понятием степеней и их свойствами.

Пример 1:

Вычислите значение выражения \(3^2 + 2 \cdot 3^3 - 4 \cdot 3^1\).

Решение:

Сначала выполним операции внутри скобок: \(3^2 = 9\), \(3^3 = 27\), \(3^1 = 3\).

Теперь подставляем полученные значения в выражение: \(9 + 2 \cdot 27 - 4 \cdot 3\).

Дальше выполняем умножение и сложение: \(9 + 54 - 12 = 51\).

Ответ: \(51\).

Пример 2:

Вычислите значение выражения \((2^3)^2 - 2^4\).

Решение:

Сначала выполним возведение в степень: \((2^3)^2 = 8^2 = 64\), \(2^4 = 16\).

Теперь подставляем полученные значения в выражение: \(64 - 16\).

Выполняем вычитание: \(64 - 16 = 48\).

Ответ: \(48\).

Пример 3:

Вычислите значение выражения \(\left(\frac{1}{3^2} + \frac{1}{3^3}

ight) \cdot 3^4\).

Решение:

Сначала выполним операции внутри скобок: \(\frac{1}{3^2} = \frac{1}{9}\), \(\frac{1}{3^3} = \frac{1}{27}\).

Сложим дроби: \(\frac{1}{9} + \frac{1}{27} = \frac{3}{27} + \frac{1}{27} = \frac{4}{27}\).

Теперь умножим полученную дробь на \(3^4 = 81\): \(\frac{4}{27} \cdot 81 = \frac{4}{243} \cdot 81 = \frac{324}{243}\).

Упростим дробь: \(\frac{324}{243} = \frac{4}{3}\).

Ответ: \(\frac{4}{3}\).