Учебная программа по геометрии в 7 классе предусматривает изучение различных свойств треугольников. Одно из наиболее интересных и важных свойств треугольника - его прямоугольность. А если мы знаем, как доказать, что треугольник является прямоугольным, то этот навык нам пригодится при решении различных задач.
Для доказательства прямоугольности треугольника 7 классов вам понадобятся знания о различных типах треугольников и их свойствах. В частности, вам нужно будет знать о прямоугольном треугольнике, в котором вершина прямого угла (90 градусов) должна быть обозначена. Обычно в учебниках используется символ "гамма" (γ), чтобы обозначить вершину прямого угла.
Одним из способов доказательства прямоугольности треугольника является применение теоремы Пифагора. Согласно этой теореме, в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Эта теорема может быть использована для проверки прямоугольности треугольника, если известны длины его сторон.
Как убедиться, что треугольник прямоугольный в 7 классе
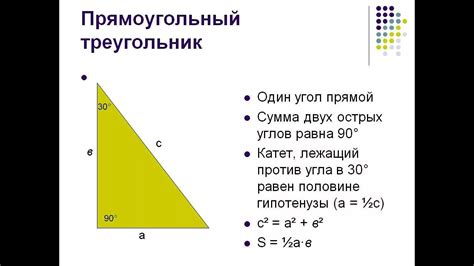
Теорема Пифагора: В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Итак, если у тебя есть треугольник со сторонами a, b и c, и ты хочешь узнать, является ли он прямоугольным, следует выполнить следующие шаги:
- Определи длины сторон треугольника.
- Возведи эти длины в квадрат.
- Сравни полученные значения: если сумма квадратов двух меньших сторон равна квадрату большей стороны, то треугольник является прямоугольным.
Если полученное уравнение не выполняется, то треугольник не является прямоугольным.
Определение треугольника прямоугольного в 7 классе

Прямоугольный треугольник - это треугольник, у которого один из углов является прямым (равным 90 градусов). Для того чтобы доказать, что треугольник является прямоугольным, необходимо использовать свойства прямоугольных треугольников.
Основное свойство прямоугольного треугольника заключается в теореме Пифагора. Эта теорема гласит, что квадрат длины гипотенузы (стороны, лежащей напротив прямого угла) равен сумме квадратов длин катетов (других двух сторон).
Используя теорему Пифагора, можно доказать, что треугольник является прямоугольным. Для этого необходимо знать длины всех трех сторон треугольника. Если квадрат наибольшей стороны равен сумме квадратов двух остальных сторон, то треугольник является прямоугольным.
Если треугольник прямоугольный, то его прямой угол помечают символом ∠
Важно помнить, что для доказательства прямоугольности треугольника необходимы все три длины сторон. Если одна сторона отсутствует или неизвестна, то нельзя утверждать, что треугольник является прямоугольным.
Типичные задачи с треугольниками в 7 классе
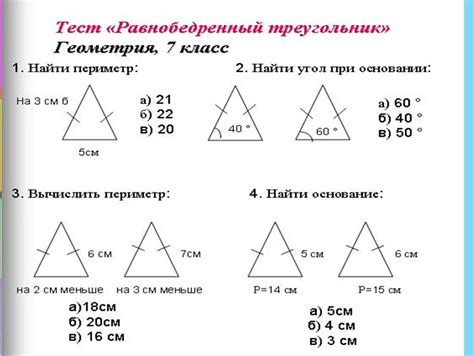
1. Определение типа треугольника по длинам его сторон и углам. В этой задаче нужно определить, является ли треугольник равносторонним, равнобедренным, прямоугольным или обычным. Для решения этой задачи необходимо знать основные определения и свойства треугольников.
2. Доказательство равенства треугольников. В этой задаче требуется доказать равенство двух треугольников по заданным условиям. Для доказательства равенства треугольников необходимо использовать свойства равенства треугольников (равенство сторон и углов).
3. Поиск недостающих сторон и углов треугольника. В этой задаче требуется найти значение недостающих сторон или углов треугольника по заданным условиям и известным данным. Для решения этой задачи необходимо использовать свойства треугольников (сумма углов треугольника, связь между углами и сторонами).
4. Построение треугольника по заданным условиям. В этой задаче требуется построить треугольник по заданным условиям (длины сторон, значения углов). Для решения этой задачи необходимо знать основные правила построения треугольников.
Эти типичные задачи помогут закрепить знания о треугольниках и развить навыки анализа геометрических объектов. Они являются основой для более сложных задач, которые будут рассматриваться в старших классах.
Методы доказательства прямоугольности треугольника

1. Теорема Пифагора
Одним из основных методов доказательства прямоугольности треугольника является применение теоремы Пифагора. Согласно этой теореме, в прямоугольном треугольнике сумма квадратов длин катетов равна квадрату длины гипотенузы. Таким образом, если известны длины сторон треугольника, можно проверить выполняется ли данное равенство и тем самым доказать его прямоугольность.
2. Признаки равенства углов
Если известны значения углов треугольника, возможно использовать признаки равенства углов в прямоугольном треугольнике. Например, если угол между катетами равен 90 градусов, а основной угол равен 45 градусов, то треугольник будет прямоугольным.
3. Геометрические свойства
Существуют также геометрические свойства, которые позволяют доказать прямоугольность треугольника. Например, если высота треугольника, проведенная из прямого угла, проходит через вершину основания, то треугольник будет прямоугольным.
4. Таблица соотношений сторон
Существуют специальные таблицы соотношений сторон в прямоугольных треугольниках, так называемые тригонометрические таблицы. Используя эти таблицы, можно определить прямоугольность треугольника, зная значения сторон и углов.
5. Использование того, что треугольник подобен другому прямоугольному треугольнику
Если треугольник подобен другому прямоугольному треугольнику, то он сам является прямоугольным. Для доказательства подобия треугольников можно использовать различные способы, например, соотношения сторон или углов.
В зависимости от доступных данных о треугольнике, можно выбрать подходящий метод доказательства его прямоугольности. Овладение этими методами позволяет корректно определить, является ли треугольник прямоугольным в 7 классе.
Правила применения теорем Пифагора и Талеса

Треугольник называется прямоугольным, если один из его углов равен 90 градусов. Для доказательства того, что треугольник прямоугольный, можно использовать теоремы Пифагора и Талеса.
- Теорема Пифагора утверждает, что в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. Данную теорему можно использовать для проверки, является ли треугольник прямоугольным. Если квадрат гипотенузы равен сумме квадратов катетов, то треугольник является прямоугольным.
- Теорема Талеса устанавливает соотношение между длинами сторон двух подобных треугольников. Эта теорема позволяет доказать, что треугольник прямоугольный, если две его стороны пропорциональны сторонам другого прямоугольного треугольника.
Для доказательства прямоугольности треугольника с помощью теоремы Пифагора можно следовать простым алгоритмом:
- Измерьте стороны треугольника и определите, какая из них является гипотенузой.
- Возведите в квадрат длины каждой стороны треугольника.
- Сравните сумму квадратов длин катетов с квадратом длины гипотенузы. Если они равны, то треугольник прямоугольный.
Для применения теоремы Талеса для доказательства прямоугольности треугольника нужно:
- Измерьте стороны треугольника и определите, какая из них является гипотенузой.
- Измерьте соответствующие стороны другого треугольника и установите их пропорциональность с соответствующими сторонами первого треугольника.
- Если две стороны треугольников пропорциональны, а третья сторона одного из треугольников является гипотенузой, то оба треугольника являются прямоугольными.
С помощью этих правил вы можете доказать, является ли треугольник прямоугольным, что поможет вам решать различные геометрические задачи.
Практические примеры решения задач на доказательство прямоугольности треугольника

- Используйте теорему Пифагора. Если известны длины сторон треугольника, можно применить теорему Пифагора для проверки прямоугольности. Теорема Пифагора гласит, что квадрат длины гипотенузы (стороны противоположной прямого угла) равен сумме квадратов длин катетов (других двух сторон треугольника). Используйте формулу a^2 + b^2 = c^2, где "а" и "b" - это длины катетов, а "с" - длина гипотенузы. Если формула выполняется, то треугольник является прямоугольным.
Используя эти методы и техники, вы сможете решить задачи на доказательство прямоугольности треугольника. Помните, что в каждой конкретной задаче могут применяться разные методы и подходы. Важно анализировать данные и использовать доступные свойства геометрии для достижения результата.



