Окружность и треугольник – две геометрические фигуры, с которыми мы сталкиваемся повседневно. Интерес представляет вопрос о вписанности треугольника в окружность. В таком случае, все вершины треугольника лежат на окружности, что создает ряд интересных свойств и отношений между его сторонами и углами. Предлагаем разобраться, как определить, вписан ли треугольник в окружность.
Основным критерием вписанности треугольника в окружность является условие, согласно которому расстояние от центра окружности до каждой из вершин треугольника должно быть одинаковым. Другими словами, отрезки, соединяющие центр окружности с каждой из вершин треугольника, должны иметь одинаковую длину. Это свойство, безусловно, свидетельствует о вписанности треугольника в окружность.
Для проверки вписанности треугольника в окружность можно использовать теорему о равенстве прямых углов. Если у нас имеется треугольник, каждый угол которого прямой, то он является вписанным в окружность. По теореме касательные, проведенные к окружности в точках пересечения сторон треугольника, являются перпендикулярами к этим сторонам. Это доказывает вписанность треугольника в окружность и является еще одним критерием, который можно использовать для проверки данного свойства.
Определение вписанности треугольника в окружность
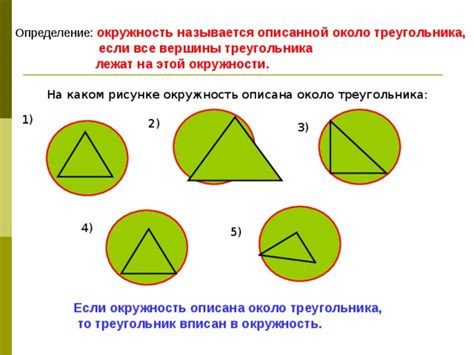
Для определения, вписан ли треугольник в окружность, необходимо провести ряд проверок:
- Проверить, что все вершины треугольника лежат на окружности.
- Убедиться, что все стороны треугольника касаются окружности.
- Проверить, что центр окружности лежит на пересечении биссектрис треугольника.
Для проверки, что вершины треугольника лежат на окружности, можно вычислить расстояние от каждой вершины до центра окружности и убедиться, что все эти расстояния равны радиусу окружности.
Проверка, что стороны треугольника касаются окружности, может быть выполнена путем проведения перпендикуляров из центра окружности к каждой стороне треугольника. Если перпендикуляры пересекают стороны треугольника в их серединах, то это говорит о том, что стороны треугольника касаются окружности.
Для проверки, что центр окружности лежит на пересечении биссектрис треугольника, необходимо найти точку пересечения биссектрис и убедиться, что эта точка совпадает с центром окружности.
Метод полупериметра

В данном методе рассматривается отношение полупериметра треугольника к радиусу окружности. Если это отношение равно 1, то треугольник является вписанным в окружность, если оно меньше 1, то треугольник невписанный.
Для реализации метода необходимо:
| Шаг | Описание |
|---|---|
| 1 | Вычислить длины сторон треугольника. |
| 2 | Вычислить полупериметр треугольника (сумма длин сторон, разделенная на 2). |
| 3 | Вычислить радиус окружности, описанной вокруг треугольника (произведение длин сторон, разделенное на 4-кратное значение площади треугольника). |
| 4 | Вычислить отношение полупериметра к радиусу окружности. |
| 5 | Сравнить полученное отношение с 1. |
Если отношение равно 1, то треугольник вписан в окружность, иначе треугольник невписанный.
Метод полупериметра является достаточно простым и эффективным способом определения, вписан ли треугольник в окружность. Он основывается на геометрических свойствах треугольника и окружности, и его можно легко реализовать в программном коде.
Метод радиусов описанной и вписанной окружностей
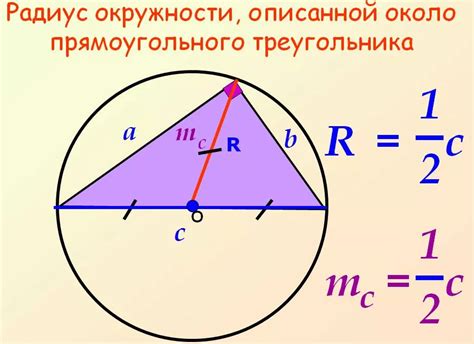
Чтобы применить этот метод, необходимо найти радиус описанной и вписанной окружностей треугольника.
Радиус описанной окружности можно найти по формуле:
Ro = a/2sinA = b/2sinB = c/2sinC
- Ro - радиус описанной окружности
- a, b, c - стороны треугольника
- A, B, C - соответствующие углы треугольника
Радиус вписанной окружности можно найти по формуле:
Ri = p/p
- Ri - радиус вписанной окружности
- p - полупериметр треугольника
- S - площадь треугольника
Если радиус описанной окружности равен радиусу вписанной окружности, то это означает, что треугольник является вписанным.
Метод радиусов описанной и вписанной окружностей является эффективным инструментом для определения, вписан ли треугольник в окружность. Он позволяет сделать это достаточно быстро и точно.
Существование вписанного треугольника
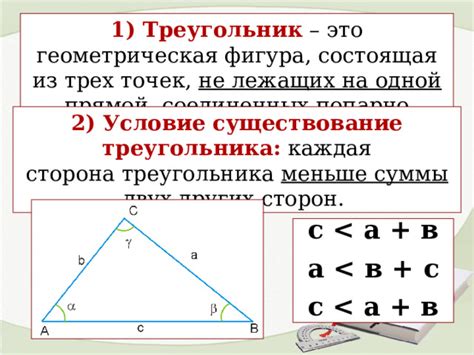
В зависимости от заданных условий, треугольник может быть вписанным в окружность или нет.
Если известны три точки треугольника, можно проверить, существует ли окружность, которая проходит через все три точки. Если да, то треугольник является вписанным.
Существуют различные методы определения вписанного треугольника, такие как:
- Использование формулы окружности и проверка, лежат ли все три точки на одной окружности.
- Использование свойства, что угол, образованный двумя хордами, равен полусумме углов, которые они отсекают на окружности.
- Проверка, являются ли все три угла треугольника прямыми углами, так как вписанный треугольник всегда является прямоугольным.
Важно помнить, что вписанный треугольник существует только в случаях, когда все условия для этого выполняются. В противном случае, треугольник не является вписанным.
Понимание существования вписанного треугольника в окружность является важным для различных математических и геометрических задач, а также для понимания связей между различными элементами треугольника и окружности.
Геометрические свойства вписанного треугольника
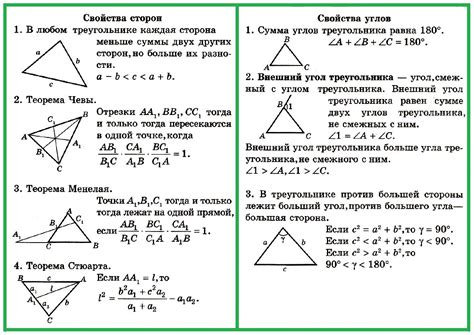
Вписанный треугольник имеет несколько уникальных свойств:
- Описанная окружность: Вокруг вписанного треугольника можно описать окружность, проходящую через все его вершины. Данная окружность называется описанной окружностью. Центр описанной окружности лежит на пересечении перпендикуляров, проведенных к серединам сторон треугольника.
- Центр вписанной окружности: Вписанный треугольник также имеет вписанную окружность, которая касается всех его сторон. Центр вписанной окружности лежит внутри треугольника и является точкой пересечения биссектрис его углов.
- Углы: Вписанный треугольник имеет интересные свойства относительно его углов. Угол, образованный хордой окружности и касательной к ней в точке касания, равен половине вписанного угла, опирающегося на ту же хорду. В данном случае, величина средней линии треугольника, проведенной из любой его вершины к середине противоположной стороны, также равна половине основания сегмента, образованного этими сторонами.
- Длины сторон: Вписанный треугольник имеет особое соотношение между длинами его сторон. Если a, b и c - длины сторон треугольника, а r - радиус вписанной окружности, то сумма длин сторон a + b + c всегда будет больше или равна удвоенному радиусу вписанной окружности 2r.
Геометрические свойства вписанного треугольника открывают возможности для решения разнообразных задач и расчетов в геометрии. Изучение и применение данных свойств может быть полезным для математического анализа и решения различных задач в области строительства, дизайна и других сферах науки и жизни.
Применение вписанных треугольников

Одним из основных свойств вписанного треугольника является то, что его вершины лежат на окружности. Это свойство позволяет использовать вписанные треугольники для нахождения различных параметров окружности, например, радиуса или длины дуги.
Вписанные треугольники также часто используются для построения геометрических конструкций. Например, с их помощью можно построить описанную окружность, проходящую через все вершины треугольника. Это свойство позволяет упростить решение некоторых задач, связанных с треугольниками.
Более того, вписанные треугольники имеют свои приложения в компьютерной графике и архитектуре. Определение и использование вписанных треугольников позволяет создавать красивые и гармоничные композиции, а также упростить конструкцию и расчет различных форм и фигур.



