Многоугольники - это фигуры, ограниченные замкнутой ломаной линией, состоящей из отрезков. Часто возникает необходимость определить, принадлежит ли заданная точка внутренности многоугольника или нет. Решение этой задачи может быть полезно во многих сферах - от компьютерной графики до геодезии.
Существуют различные методы определения принадлежности точки многоугольнику. Один из наиболее распространенных методов - это алгоритм пересечения линий. Его суть заключается в том, чтобы провести линию из данной точки в любую сторону, и посчитать количество пересечений этой линии с ребрами многоугольника. Если количество пересечений нечетное, то точка находится внутри многоугольника, если четное - вне его.
Существуют и другие методы определения принадлежности точки многоугольнику, например, метод векторных произведений или метод проверки наличия точки на одном из углов многоугольника. Каждый из этих методов имеет свои преимущества и недостатки, и выбор метода зависит от конкретных требований и условий задачи.
Определение принадлежности точки многоугольнику
Алгоритм "точка внутри многоугольника" основан на следующей идее: если провести линию из данной точки в любую другую точку на плоскости и подсчитать количество пересечений с границей многоугольника, то, в зависимости от четности или нечетности этого количества, можно определить, внутри или снаружи многоугольника находится данная точка.
Для реализации этого алгоритма необходимо выполнить следующие шаги:
- Установить начальное значение переменной-счетчика количества пересечений в ноль.
- Проити по всем сторонам многоугольника.
- Для каждой стороны проверить, пересекается ли она с прямой, проведенной из данной точки и направленной вправо.
- Если сторона пересекается, увеличить значение счетчика.
- Если количество пересечений нечетное, то точка лежит внутри многоугольника. Иначе, она находится снаружи.
Этот алгоритм работает для простых и выпуклых многоугольников. Однако, для сложных или самопересекающихся многоугольников, его применение может привести к неверному результату. В таких случаях, необходимо использовать другие алгоритмы для определения принадлежности точки многоугольнику.
Простой вариант решения

Определение принадлежности точки внутренности многоугольнику можно осуществить с помощью простого алгоритма.
Шаги алгоритма:
- Построить отрезки, соединяющие каждую вершину многоугольника с заданной точкой.
- Подсчитать количество пересечений отрезков с горизонтальной прямой, проходящей через заданную точку и не пересекающую многоугольник.
- Если количество пересечений нечетное, то точка находится внутри многоугольника.
- Если количество пересечений четное, то точка находится снаружи многоугольника.
Данный алгоритм работает для произвольного многоугольника, однако необходимо быть внимательными при выборе точек на границе многоугольника, так как они могут находиться как внутри, так и снаружи.
Алгоритм пересечения луча
Для начала необходимо определить, является ли точка внутренней или внешней точкой многоугольника. Для этого проводится прямая линия (луч) из этой точки в любом направлении. Затем считается количество пересечений этого луча со сторонами многоугольника.
Если количество пересечений четное, то точка находится вне многоугольника, если нечетное – внутри многоугольника.
Описание алгоритма:
1. Построение луча, проведение линии из определяемой точки (x0, y0) в бесконечность в направлении, отличном от оси OX.
2. Подсчет количества пересечений луча со сторонами многоугольника.
3. Если количество пересечений четное, то точка находится вне многоугольника. Если количество пересечений нечетное, то точка находится внутри многоугольника.
Алгоритм пересечения луча является достаточно простым и эффективным способом определения принадлежности точки внутренности многоугольнику. Он может быть применен в различных областях, где требуется определение принадлежности точек. Этот алгоритм можно реализовать с использованием различных программных языков и технологий.
Алгоритм поиска пересечений
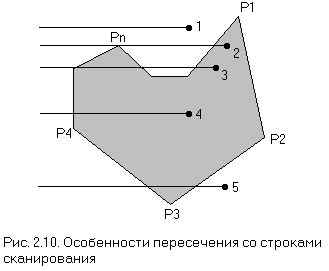
При определении принадлежности точки внутренности многоугольнику может возникнуть необходимость в поиске пересечений. Пересечения могут возникнуть, когда луч, проведенный из точки, пересекает одну или несколько граней многоугольника.
Для поиска пересечений можно использовать алгоритм пересечения луча с отрезком. Алгоритм заключается в последовательном переборе всех граней многоугольника и проверке их пересечения с лучом.
Алгоритм пересечения луча с отрезком может быть реализован следующим образом:
- Для каждого отрезка, образующего грань многоугольника:
- Проверить, пересекает ли луч отрезок. Для этого можно использовать формулу пересечения луча с отрезком.
- Если луч пересекает отрезок, определить точку пересечения.
- Запомнить точку пересечения и продолжить перебор остальных отрезков.
После завершения алгоритма, будут найдены все точки пересечения луча с гранями многоугольника. Полученные точки пересечения могут быть использованы для дальнейшей проверки принадлежности точки многоугольнику.
Усложнение задачи: многоугольник с самопересечениями
Многоугольник с самопересечениями представляет собой фигуру, у которой стороны пересекаются друг с другом. Такие многоугольники могут быть сложными для решения задачи определения принадлежности точки внутренности.
При наличии самопересечений сторон многоугольника возникает несколько особых ситуаций:
- Если точка лежит на самопересекающейся стороне многоугольника, то её принадлежность не определена однозначно, поскольку можно допустить различные варианты пути от одной стороны многоугольника к другой.
- Если точка находится внутри области самопересечения, то её принадлежность также не определена, поскольку можно провести бесконечное количество путей для достижения данной точки.
- Если точка находится внутри многоугольника, но вне его самопересекающихся сторон, то принадлежность точки определяется по привычным алгоритмам.
Решение задачи определения принадлежности точки внутренности многоугольнику с самопересечениями является более сложной и требует применения алгоритмов, специально рассчитанных для обработки таких случаев.
Примечание: В реальных приложениях, как правило, избегают использования самопересекающихся многоугольников, поскольку они могут вызывать проблемы при обработке их в программных системах или визуализации на экране.
Алгоритм обхода ребер многоугольника

Для определения принадлежности точки внутренности многоугольнику необходимо применить алгоритм обхода его ребер. Алгоритм состоит из следующих шагов:
- Выбрать произвольную точку внутри многоугольника и установить текущее положение.
- Найти пересечение текущего положения с каждым ребром многоугольника.
- Записать точку пересечения в таблицу.
- Изменить текущее положение на точку пересечения.
- Повторить шаги 2-4 для всех ребер многоугольника.
- Если количество пересечений четное, то точка лежит вне многоугольника, иначе - внутри.
Таблица, в которую записываются точки пересечения, представляет собой двухколоночный список, где в первой колонке указывается координата X точки, а во второй - координата Y.
Этот алгоритм обладает линейной сложностью и позволяет определить принадлежность точки внутренности многоугольнику с высокой точностью.



