Перпендикулярность векторов – важное понятие в линейной алгебре и геометрии. Она используется для нахождения углов между векторами, а также для решения многих задач в различных областях знаний. Знание способов определения перпендикулярности векторов является необходимым для понимания и решения множества задач, связанных с аналитической геометрией.
Определение перпендикулярности векторов может быть дано в несколько формах. Одним из методов является проверка равенства нулю скалярного произведения данных векторов. Если скалярное произведение равно нулю, то векторы перпендикулярны между собой.
Векторы в трехмерном пространстве можно задать с помощью координат. Но как определить перпендикулярность векторов по их координатам? Существует простой метод: если векторы заданы в виде координат, то их координаты можно сравнить. Векторы будут перпендикулярными, если определители, составленные из координат этих векторов, равны нулю.
Определение перпендикулярности векторов

Чтобы определить, являются ли два вектора перпендикулярными, можно воспользоваться геометрической и аналитической методиками.
Геометрический метод предполагает нахождение угла между векторами. Если угол равен 90 градусам, то векторы являются перпендикулярными.
Аналитический метод основывается на свойствах векторного произведения. Если векторное произведение двух векторов равно нулю, то они перпендикулярны друг другу.
Для определения перпендикулярности векторов по их координатам следует вычислить их скалярное произведение и проверить, равно ли оно нулю:
a · b = 0
Если выражение выполняется, то векторы a и b перпендикулярны.
Это простой способ определить, являются ли векторы перпендикулярными, используя их координаты.
Векторы в трехмерном пространстве
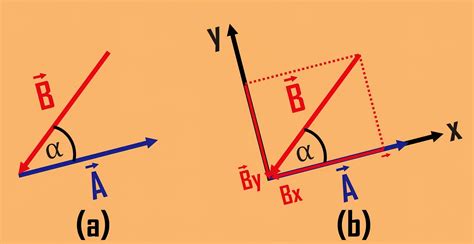
Каждый вектор в трехмерном пространстве можно представить с помощью трех координат: x, y и z. Эти координаты описывают положение вектора в трехмерной системе координат. При задании вектора в координатной форме, его направление и длина могут быть определены исходя из этих координат.
Векторы в трехмерном пространстве могут быть складываться и вычитаться друг из друга, а также умножаться на скаляры. Сложение векторов происходит покоординатно: x-координаты складываются, y-координаты складываются, и z-координаты складываются. Аналогично, вычитание и умножение на скаляр также выполняются покоординатно.
Перпендикулярность векторов в трехмерном пространстве определяется с помощью их скалярного произведения. Два вектора A и B являются перпендикулярными, если и только если их скалярное произведение равно нулю. Другими словами, если A = (a1, a2, a3) и B = (b1, b2, b3), то A и B перпендикулярны, если a1*b1 + a2*b2 + a3*b3 = 0.
Перпендикулярность векторов имеет важное значение во многих областях, например, при определении ортогональности плоскостей или при решении задач на геометрическое положение объектов в трехмерном пространстве.
Пример:
Пусть у нас есть два вектора: A = (1, 2, 3) и B = (-2, 1, 0). Для определения их перпендикулярности, мы вычисляем их скалярное произведение:
A · B = (1)(-2) + (2)(1) + (3)(0) = -2 + 2 + 0 = 0
Таким образом, векторы A и B являются перпендикулярными.
Понимание свойств и характеристик векторов в трехмерном пространстве является важным для решения различных математических и физических задач. Это позволяет нам лучше визуализировать и понимать объекты и процессы, происходящие в трехмерном пространстве.
Условия перпендикулярности

x1*x2 + y1*y2 + z1*z2 = 0
Таким образом, чтобы проверить, перпендикулярны ли два вектора, необходимо вычислить их скалярное произведение и проверить, равно ли оно нулю.
Геометрическая интерпретация
Геометрическая интерпретация перпендикулярности векторов базируется на представлении векторов в виде отрезков прямых на плоскости или в пространстве. Если два вектора перпендикулярны, то они образуют прямой угол друг с другом.
Для определения перпендикулярности векторов по их координатам можно использовать следующий алгоритм:
- Рассмотрим два вектора в виде отрезков прямых на плоскости или в пространстве.
- Измерим угол между этими векторами при помощи специального инструмента, например, универсального угломера.
- Если полученный угол равен 90 градусов, то векторы являются перпендикулярными.
- Если полученный угол не равен 90 градусам, то векторы не являются перпендикулярными.
Таким образом, геометрическая интерпретация позволяет определить перпендикулярность векторов, исходя из их угла между собой.
Вычисление скалярного произведения

S = x1 * x2 + y1 * y2 + z1 * z2
где:
- S - результат скалярного произведения
- x1, y1, z1 - координаты первого вектора
- x2, y2, z2 - координаты второго вектора
Скалярное произведение может принимать значения отрицательные, положительные или нулевые. Оно равно нулю, если векторы перпендикулярны друг другу, и принимает максимальное значение, если векторы сонаправлены.
Формула скалярного произведения

Для двух векторов a и b в трехмерном пространстве формула скалярного произведения имеет вид:
a · b = ax * bx + ay * by + az * bz |
Где ax, ay и az – координаты вектора a, а bx, by и bz – координаты вектора b.
Если скалярное произведение равно нулю (a · b = 0), то векторы ортогональны, а значит, перпендикулярны друг другу.
Скалярное произведение и перпендикулярность

Формула для вычисления скалярного произведения двух векторов в координатной форме выглядит следующим образом:
| a · b = a₁ * b₁ + a₂ * b₂ + a₃ * b₃ |
где a₁, a₂, a₃ и b₁, b₂, b₃ - координаты векторов a и b соответственно.
Если скалярное произведение двух векторов равно нулю:
| a · b = 0 |
то это означает, что векторы a и b перпендикулярны друг другу. Иными словами, двухмерные векторы будут перпендикулярными, если их координатное произведение будет равно нулю.
С помощью скалярного произведения и его равенства нулю можно определить перпендикулярность векторов, что широко используется в различных областях науки и техники. Например, в физике и геометрии, знание перпендикулярности векторов позволяет решать задачи на построение перпендикуляров, нахождение углов между векторами и другие геометрические задачи.
Вычисление векторного произведения

Для вычисления векторного произведения векторов a и b можно воспользоваться следующей формулой:
a × b = |a| |b| sin(θ) n
- a и b – исходные векторы
- |a| и |b| – длины векторов a и b
- θ – угол между векторами a и b
- n – вектор, перпендикулярный плоскости, образованной a и b
Таким образом, чтобы определить, являются ли два вектора перпендикулярными, необходимо вычислить их векторное произведение и проверить его равенство нулю. Если векторное произведение равно нулю, то векторы a и b перпендикулярны.
Векторное произведение имеет несколько свойств, которые могут быть полезны при его вычислении:
- Если векторы a и b коллинеарны, то их векторное произведение равно нулю.
- Векторное произведение антикоммутативно, то есть a × b = -b × a.
- Длина вектора, полученного в результате векторного произведения a и b, равна |a| |b| sin(θ), где θ – угол между векторами.
Формула векторного произведения

Формула векторного произведения используется для определения перпендикулярности векторов по их координатам. Она позволяет найти новый вектор, который перпендикулярен исходным векторам.
Пусть у нас есть два вектора: a и b. Тогда формула векторного произведения имеет вид:
a × b = (a2 * b3 - a3 * b2, a3 * b1 - a1 * b3, a1 * b2 - a2 * b1)
где a1, a2, a3 и b1, b2, b3 - координаты векторов a и b соответственно.
Таким образом, если результат векторного произведения равен нулю, то исходные векторы a и b перпендикулярны друг другу.



