Ортогональная проекция - это процесс преобразования трехмерных объектов в двумерное пространство путем отражения точек на плоскости. Когда речь идет о прямой, ортогональная проекция делает возможным представление ее на плоскости в виде отрезка, сохраняя все основные свойства и отношения.
Ортогональная проекция применяется в различных областях, включая графику, инженерию и архитектуру. Она позволяет представить сложные трехмерные модели в более простом и понятном виде. Например, отрезок прямой, который является проекцией боковой грани параллелепипеда, может служить основой для построения плоских чертежей зданий или машин.
Давайте рассмотрим пример ортогональной проекции прямой на плоскость. Представим себе прямую, заданную уравнением y = 2x + 1, и плоскость, заданную уравнением z = 3. Чтобы найти ортогональную проекцию прямой на плоскость, мы должны найти точку пересечения прямой и плоскости. Сначала найдем эту точку, подставив значения y и z из уравнений прямой и плоскости соответственно: 2x + 1 = 3. Решив это уравнение, мы получаем x = 1.
Что такое ортогональная проекция?

Ортогональная проекция применяется в различных областях, таких как инженерное дело, архитектура и компьютерная графика. Она позволяет упростить сложные трехмерные модели и представить их в удобном для анализа и визуализации двумерном виде.
Проекция может быть осуществлена на различные плоскости. Например, ортогональная проекция прямой на плоскость XY даст ее изображение в виде отрезка, перпендикулярного плоскости XY. Точки линии будут отображены на плоскость с сохранением их расположения и относительных расстояний.
Ортогональная проекция позволяет визуализировать и анализировать пространственные объекты в двухмерном виде, что делает ее полезной инструментом для проектирования и построения.
Ортогональная проекция: определение и особенности
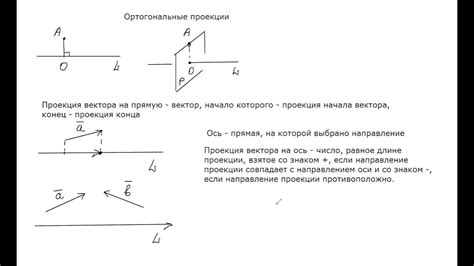
Ортогональная проекция широко применяется в графике, инженерии и архитектуре. Проекция позволяет упростить изображение сложных трехмерных конструкций и анализировать их особенности. Ортогональная проекция также используется для создания чертежей, планов зданий и машин, а также для моделирования пространственных объектов в компьютерной графике.
Особенностью ортогональной проекции является то, что она сохраняет углы между прямыми и плоскостями при проецировании. Это значит, что если в трехмерном пространстве две прямые или плоскости образуют определенный угол, то этот угол будет сохранным и на плоскости проекции.
Ортогональная проекция имеет несколько видов, включая проекцию параллельных линий (точка пересечения прямых параллельна плоскости проекции), проекцию перпендикулярных линий (точка пересечения прямых перпендикулярна плоскости проекции) и проекцию точки (точка пространства отображается в соответствующую точку плоскости).
Ортогональная проекция имеет много применений в нашей повседневной жизни. Она помогает инженерам создавать точные чертежи и модели, а архитекторам – представлять сложные здания и пространства. Ортогональная проекция также используется в компьютерной графике и визуализации, где она позволяет создавать реалистичные трехмерные модели и виртуальные миры.
Ортогональная проекция прямой на плоскость: основные моменты

Для вычисления ортогональной проекции прямой на плоскость необходимо знать координаты точек, через которые проходит прямая, а также вектор нормали к плоскости.
Основной момент ортогональной проекции заключается в том, что она позволяет упростить работу с трехмерными объектами, представляя их на двумерной плоскости. Это особенно полезно при решении различных геометрических задач, таких как построение, нахождение расстояния до прямой и т.д.
Проекция прямой на плоскость может быть представлена в виде собственной формулы, которая позволяет точно определить координаты проекции на плоскости. Формула зависит от выбранного базиса и может быть уточнена с помощью математических методов и дополнительных условий.
Примером ортогональной проекции прямой на плоскость может служить строительство. Проекция стен и фундамента здания на плоскость позволяет более точно определить их положение и размеры. Также ортогональная проекция применяется в картографии и компьютерной графике для отображения трехмерных объектов на двумерном экране.
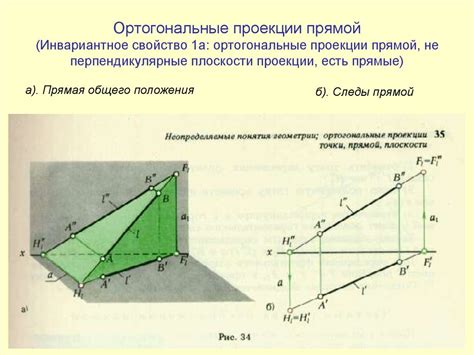
Примеры ортогональной проекции прямой на плоскость
| Пример | Описание |
|---|---|
| Проекция окружности на плоскость | Если прямая является осью окружности, ее ортогональная проекция на плоскость будет представлять собой эллипс с осями, параллельными осям плоскости. |
| Проекция прямой на горизонтальную плоскость | Если прямая находится в вертикальной плоскости, ее ортогональная проекция на горизонтальную плоскость будет представлять собой отрезок, горизонтальный по отношению к плоскости. |
| Проекция прямой на наклонную плоскость | Если прямая находится в наклонной плоскости, ее ортогональная проекция на эту плоскость будет представлять собой отрезок, перпендикулярный плоскости. |
Это лишь несколько примеров ортогональной проекции прямой на плоскость. В реальных задачах может быть множество ситуаций, когда необходимо проектировать прямую на плоскость, и ортогональная проекция является одним из способов достижения этой цели.
Пример 1: проекция прямой перпендикулярна плоскости
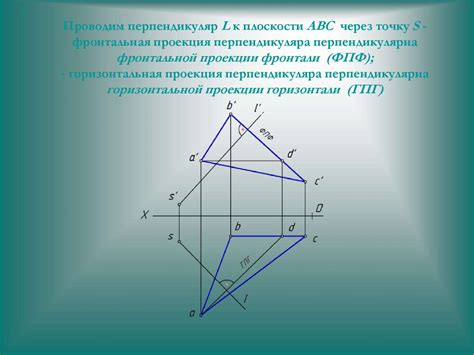
Предположим, у нас есть прямая линия и плоскость. Мы хотим найти ортогональную проекцию этой прямой на плоскость.
В данном примере предположим, что прямая линия проходит через точку A(2, 3, 1) и точку B(4, 1, 2), а плоскость задана уравнением 2x + y - z = 0.
Для начала, нам необходимо найти вектор нормали к плоскости, который является перпендикулярным к плоскости. Используя коэффициенты уравнения плоскости, мы получаем вектор нормали N(2, 1, -1).
Затем мы должны найти вектор направления прямой, который можно получить из координат точек A и B. Используя формулу для вычисления вектора направления, мы получаем вектор D(2, -2, 1).
Ортогональная проекция прямой на плоскость будет лежать на плоскости и будет параллельна вектору нормали N.
Используя формулу для нахождения проекции вектора на другой вектор, мы получаем проекцию вектора D на вектор N:
P = (D • N /



