Многие функции имеют особенность - они могут быть либо четными, либо нечетными. Четная функция обладает свойством симметрии относительно оси ординат, то есть f(x) = f(-x) для любого значения x. Нечетная функция же обладает свойством симметрии относительно начала координат, то есть f(x) = -f(-x) для любого значения x.
Для определения, является ли функция четной или нечетной, нужно проанализировать ее алгебраическую формулу. Если при подстановке -x вместо x функция остается неизменной, то она является четной. Если же знак функции меняется при подстановке -x, то она является нечетной. Это свойство функции может быть полезным при решении различных задач и определении их особенностей.
Однако, есть и функции, которые не являются ни четными, ни нечетными. В таких случаях нужно применять дополнительные методы анализа. Например, можно разложить функцию в ряд Тейлора и проверить, остаются ли все нечетные степени одинаково нулевыми. Если нет, то функция не является ни четной, ни нечетной.
Определение нечетной функции
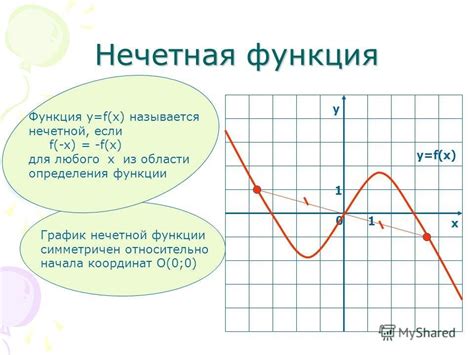
Для этого применяем следующий алгоритм:
| Шаг | Действие | Результат |
|---|---|---|
| 1 | Подставляем вместо x значение -x | Получаем f(-x) |
| 2 | Вычисляем значение функции f при x | Получаем f(x) |
| 3 | Умножаем значение функции f(x) на -1 | Получаем -f(x) |
| 4 | Сравниваем полученные значения f(-x) и -f(x) |
|
Если функция не является нечетной, то можно проверить, является ли она четной или ни одним из этих видов функций. Для этого нужно выполнить аналогичные действия, но сравнивать значения f(-x) и f(x). Если они равны, то функция является четной. Если значения не равны, то функция не является ни четной, ни нечетной, а следовательно, обладает произвольными свойствами.
Определение четной функции

Четной функцией называется функция, которая удовлетворяет следующему условию:
| f(x) = f(-x) |
То есть, если значение функции в точке x равно значению функции в точке -x, то функция считается четной.
У четной функции ось симметрии проходит через начало координат (0,0). График четной функции симметричен относительно оси ординат. При этом, если функция является четной и график функции трехмерный, то он симметричен относительно плоскости XOY.
Если функция не является ни четной, ни нечетной, то она может быть общей функцией. В этом случае ее график не обладает ни осевой, ни центральной симметрией. Общие функции могут принимать значения как на положительной полуоси, так и на отрицательной.
Что делать, если функция не является ни нечетной, ни четной
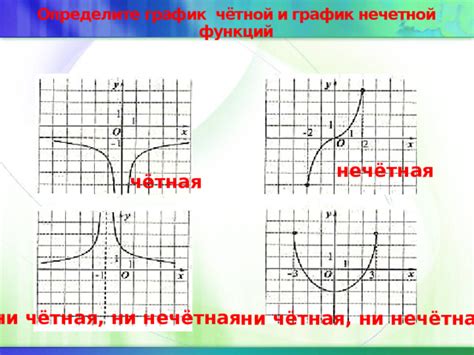
Возможные действия при исследовании такой функции:
| Шаг | Описание |
|---|---|
| 1 | Определить область определения функции, то есть найти множество значений аргумента, при которых функция определена. |
| 2 | Исследовать поведение функции на границах области определения, чтобы выяснить ее свойства в этих точках. |
| 3 | Найти точки разрыва функции, если они есть, и проанализировать ее свойства в этих точках. |
| 4 | Выяснить, является ли функция монотонной на интервалах области определения. |
| 5 | Исследовать функцию на наличие экстремумов и точек перегиба. |
В результате проведенных исследований можно получить информацию о поведении функции и использовать ее в дальнейшем анализе. Необходимо учесть, что функция может обладать различными свойствами и выявление их требует детального анализа. Поэтому, при исследовании функции, не являющейся ни нечетной, ни четной, важно проводить все шаги анализа и учитывать все возможные особенности функции.



