Один из фундаментальных навыков, которые требуются в математике, это умение находить значения выражений. Этот навык развивается со временем, поэтому восьмой класс - прекрасная возможность улучшить его - понять, как раскрывается значение выражения и как его вычислить.
Выражение - это математическая комбинация чисел, переменных и операторов, таких как знаки сложения, вычитания, умножения или деления. Но как определить, чему равно выражение? Процесс нахождения значения выражения включает в себя замену переменных на известные числа и выполнение операций по порядку.
Например, рассмотрим простое выражение: 2 + 3 * 4. Чтобы найти его значение, сначала умножим 3 на 4, получим 12, а затем сложим 2 с 12 и получим 14. Значение выражения равно 14. Это важно знать и понимать, так как при решении уравнений и задач, значения выражений помогают выявить правильные ответы.
Найдите значение выражения в 8 классе

Значение выражения - это число, которое получается в результате его вычисления. Чтобы найти значение выражения, нужно заменить переменные числами и выполнить все вычисления внутри скобок, по правилам приоритета операций.
Например, рассмотрим выражение 3 * (4 + 2). Для его вычисления, мы сначала выполняем операцию в скобках 4 + 2, получаем 6, а затем умножаем его на 3. Таким образом, значение выражения равно 18.
Другой пример - выражение 10 - (3 * 2) / 4. Здесь, внутри скобок выполняется умножение 3 * 2, получаем 6. Затем деление 6 на 4 дает нам 1.5. И наконец, вычитание 10 - 1.5 равно 8.5.
Важно помнить, что в выражениях также могут применяться различные математические операции, такие как сложение, вычитание, возведение в степень, извлечение корня и др. Правильное выполнение всех операций и последовательность их применения помогут найти правильное значение выражения.
Таким образом, нахождение значения выражения в 8 классе - это несложная задача, требующая понимания правил приоритета операций и правильного выполнения математических операций. Этот навык будет полезен для решения более сложных задач, которые ждут вас в дальнейшем обучении математике.
Понятие "значение"

В математике понятие "значение" означает результат вычисления выражения или функции. Значение может быть числовым или символьным, в зависимости от задачи и типа данных, используемых в выражении.
Примеры:
1. Дано выражение 2 + 3. Чтобы найти его значение, нужно сложить числа 2 и 3, получив в результате значение 5.
2. Рассмотрим выражение a + b, где a = 4 и b = 7. Значение этого выражения будет равно 4 + 7 = 11.
3. Функция f(x) = 3x^2 + 2 определена для любого значения переменной x. Например, при x = 2, значение функции будет равно 3*2^2 + 2 = 14.
Значение выражения или функции может быть использовано в различных математических операциях и задачах, например, для построения графиков, решения уравнений или анализа данных. Понимание понятия значения является важным элементом в изучении математики и других точных наук.
Методы нахождения значения выражения

| Метод | Описание | Пример |
|---|---|---|
| Подстановка значения переменных | Замена переменных числовыми значениями и последующее вычисление | Выражение: 2x + 5Значение x: 3Вычисление: 2(3) + 5 = 6 + 5 = 11 |
| Использование таблицы значений | Составление таблицы со значениями переменных и вычисление выражения для каждой комбинации | Выражение: 3x + yЗначения x и y: x: {1, 2, 3}y: {4, 5}Вычисление: 3(1) + 4 = 73(1) + 5 = 83(2) + 4 = 103(2) + 5 = 113(3) + 4 = 133(3) + 5 = 14 |
| Использование графиков | Построение графика функции и нахождение значения на основе координатной сетки | Выражение: 4x - 3Значение x: 2На графике: соответствует точке с координатами (2, 5)Значение: 5 |
Эти методы позволяют учащимся более наглядно представлять значения выражений и проверять правильность своих решений. Каждый из них имеет свои преимущества и применяется в зависимости от конкретной задачи.
Примеры решения задач
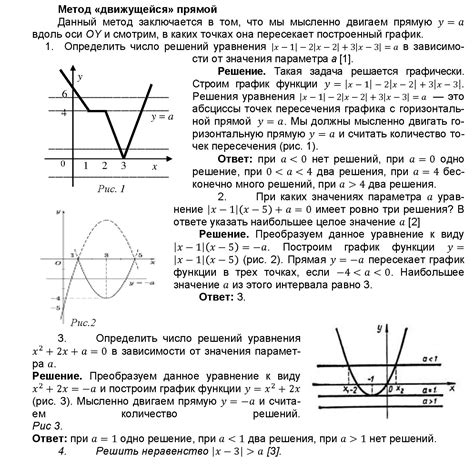
Для наглядности и лучшего понимания, предоставим несколько примеров решения задач по вычислению значения выражений в 8 классе.
Пример 1:
Вычислить значение выражения: 2 * (4 + 3) - 5 / 2.
Решение:
Сначала выполняем операцию в скобках: 4 + 3 = 7.
Затем умножаем полученный результат на 2: 2 * 7 = 14.
Далее выполняем деление: 5 / 2 = 2.5.
И, наконец, вычитаем результат деления из полученного ранее результата: 14 - 2.5 = 11.5.
Ответ: 11.5.
Пример 2:
Вычислить значение выражения: 3 * (8 - 4) + 2^2.
Решение:
Сначала выполняем операцию в скобках: 8 - 4 = 4.
Затем возводим 2 в степень 2: 2^2 = 4.
Далее умножаем результат вычитания на 3: 3 * 4 = 12.
И, наконец, прибавляем полученный результат к результату возведения в степень: 12 + 4 = 16.
Ответ: 16.
Таким образом, решая подобные задачи, следует последовательно выполнять операции по приоритету: сначала внутри скобок, затем возведение в степень, затем умножение и деление, и, наконец, сложение и вычитание.
Значение выражения в 8 классе: итоги

Значение выражения обычно находится путем замены переменных или чисел, указанных в выражении, на их соответствующие значения и последующего выполнения операций.
Например, рассмотрим следующее выражение:
3 * x + 10
Для того чтобы найти значение этого выражения, нужно заменить переменную x на ее значение и выполнить указанные операции. Например, если x = 2, то
3 * 2 + 10 = 6 + 10 = 16
Таким образом, значение данного выражения при x = 2 равно 16.
Важно уметь правильно выполнять операции с переменными и числами, а также учитывать особенности порядка операций, чтобы получить правильный ответ. Ученики также учатся решать уравнения и системы уравнений, находя значения неизвестных.
Расчеты значений выражений в 8 классе помогают развивать логическое мышление, математическую скорость и точность подсчетов. Постепенно уровень сложности выражений возрастает, и ученики запоминают все больше правил и алгоритмов для нахождения значений.
Помимо определения значений выражений, в 8 классе также изучают сведения о числах и их типах, анализируют графики функций и решают задачи на применение математических методов в реальной жизни.
Таким образом, изучение и нахождение значений выражений в 8 классе является важным этапом в обучении математике и подготовке учеников к изучению более сложных математических концепций.



