Прямоугольники – это одна из самых распространенных и изучаемых геометрических фигур. Они применяются в различных областях науки, техники и дизайна. Одним из важных аспектов изучения прямоугольников является понимание свойств и характеристик их сторон. Один из вопросов, который может возникнуть при работе с прямоугольниками – это вопрос о равенстве сторон.
Доказательство равенства сторон прямоугольника может потребовать использования различных методов и правил геометрии. В данной статье мы рассмотрим несколько простых и эффективных способов, которые помогут вам доказать равенство сторон в прямоугольнике.
Равенство сторон прямоугольника - важное понятие
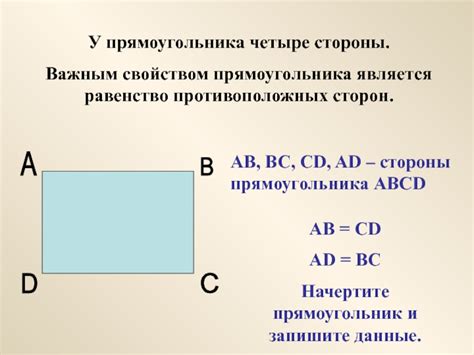
Доказательство равенства сторон прямоугольника может быть выполнено с помощью различных методов и правил геометрии. Одним из самых простых способов является использование свойств противоположных сторон прямоугольника.
- Свойство 1: Противоположные стороны прямоугольника равны.
- Свойство 2: Диагонали прямоугольника равны и делят его на два равных треугольника.
- Свойство 3: Противоположные углы прямоугольника равны.
Используя данные свойства, можно провести доказательства равенства сторон прямоугольника. Например, если известна одна из сторон и диагональ прямоугольника, то можно использовать свойство 2, чтобы найти длины оставшихся сторон. Также можно использовать свойство 3, чтобы доказать равенство углов и, следовательно, равенство соответствующих сторон.
Равенство сторон прямоугольника является важным понятием, поскольку оно позволяет нам лучше понимать геометрические свойства этой фигуры. Кроме того, это понятие имеет практическое применение в различных областях, включая архитектуру, строительство и дизайн. Поэтому важно уметь доказывать равенство сторон прямоугольника и понимать его значение в контексте геометрии.
Способы доказательства равенства сторон
Существует несколько простых и эффективных способов доказательства равенства сторон в прямоугольнике. Ниже приведены несколько из них:
1) Диагональ делит прямоугольник на два равных треугольника: Если провести диагональ прямоугольника, она разделит его на два равных треугольника. Поскольку треугольники равны, их стороны должны быть равны.
2) Противоположные стороны прямоугольника параллельны и равны: В прямоугольнике противоположные стороны всегда параллельны и равны друг другу. Если мы можем доказать этот факт, то равенство сторон будет очевидно.
3) Признак равенства сторон: Если можно показать, что две стороны прямоугольника равны друг другу, то остальные стороны также будут равны. Например, если сторона AB равна стороне CD, а сторона BC равна стороне AD, то AB = CD = BC = AD.
Использование одного или нескольких из этих способов может помочь доказать равенство сторон прямоугольника и убедиться в его геометрической симметрии и пропорциональности.
Использование геометрических фигур
Геометрические фигуры играют важную роль в математике и могут быть полезными при доказательстве равенства сторон прямоугольника. Вот несколько примеров, как использовать некоторые геометрические фигуры для этой цели:
1. Квадраты: при наличии квадратов со сторонами, равными сторонам прямоугольника, можно сравнить их площади. Если площади квадратов равны, то и стороны прямоугольника равны.
2. Прямоугольники: можно создать несколько прямоугольников с помощью дополнительных линий или разделением прямоугольника на несколько частей. Затем можно сравнить площади этих прямоугольников. Если площади прямоугольников равны, то и стороны прямоугольника равны.
3. Треугольники: можно использовать разные виды треугольников для доказательства равенства сторон прямоугольника. Например, равнобедренный треугольник может быть сконструирован так, чтобы его боковые стороны были равны сторонам прямоугольника. Затем можно сравнить площади этих треугольников. Если площади треугольников равны, то и стороны прямоугольника равны.
| Пример использования геометрических фигур: | Иллюстрация: |
|---|---|
| Сравнение площадей квадратов |  |
| Сравнение площадей прямоугольников |  |
| Использование равнобедренного треугольника |  |
Рассмотрение углов и диагоналей
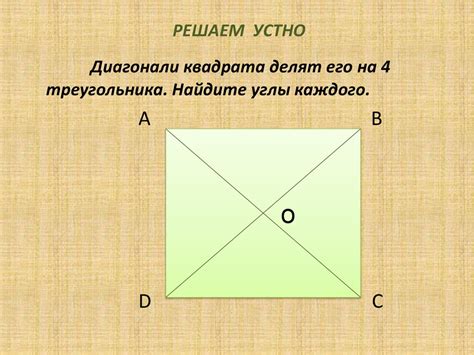
Для доказательства равенства сторон прямоугольника можно применить рассмотрение его углов и диагоналей.
У прямоугольника все углы равны между собой и равны 90 градусам. Это означает, что каждый угол на противоположных сторонах прямоугольника должен быть равным соответствующему углу на другой параллельной стороне.
Если известно, что в прямоугольнике есть две диагонали, можно использовать их свойства для доказательства равенства сторон. Диагонали прямоугольника являются его характерными элементами и всегда пересекают друг друга в точке, которая делит каждую диагональ на две равные части. Исследуя диагонали прямоугольника, можно обнаружить, что они равны между собой, и, следовательно, прямоугольник является равнобоким. Это означает, что все его стороны равны друг другу.
Исходя из рассмотренных свойств углов и диагоналей, можно заключить, что равество сторон прямоугольника доказывается с использованием геометрических свойств фигуры.
Измерение сторон и углов прямоугольника
Для доказательства равенства сторон прямоугольника необходимо иметь точные измерения длины каждой из сторон. Для этого можно использовать инструменты измерения, такие как линейка или метр. Обычно стороны прямоугольника измеряются в сантиметрах или метрах.
Для измерения длины стороны прямоугольника необходимо поместить линейку или метр вдоль стороны и считывать измерение на ее шкале. Важно помнить, что измерение должно быть точным, чтобы доказательство равенства было корректным.
Для измерения углов прямоугольника можно использовать угломер или гониометр. Эти инструменты позволяют точно измерить угол между двумя сторонами прямоугольника. Важно помнить, что прямоугольник имеет два прямых угла, которые равны 90 градусам. Если измерения показывают, что углы прямоугольника равны 90 градусам, то это также является доказательством равенства сторон.
Проверка равенства сторон с помощью формул
Существует несколько простых формул, которые можно использовать для проверки равенства сторон прямоугольника. Эти формулы основаны на свойствах прямоугольника и его геометрии.
Если у нас есть прямоугольник ABCD, где AB - основание, BC - высота, и CD - диагональ, мы можем использовать следующие формулы:
1. Формула равенства сторон: AB = CD. Если основание прямоугольника равно его диагонали, то все стороны прямоугольника будут равны.
2. Формула равенства сторон: AB = BC. Если основание прямоугольника равно его высоте, то прямоугольник будет квадратом, и все его стороны будут равны.
3. Формула для нахождения длины диагонали: CD = √(AB^2 + BC^2). С помощью этой формулы можно проверить, равны ли основание и диагональ прямоугольника.
Используя данные формулы, можно убедиться в равенстве сторон прямоугольника. Это может быть полезно при решении геометрических задач или проверке правильности прямоугольного объекта.



