Существует несколько эффективных методов доказательства равенства и параллельности сторон. Один из наиболее простых и часто используемых методов - метод сопоставления. Этот метод основывается на использовании одной или нескольких уже доказанных фигур, которые сравниваются с другими фигурами для определения равенства или параллельности сторон.
Еще одним популярным методом доказательства равенства сторон является метод измерения. Этот метод предполагает использование геометрических инструментов, таких как линейка или угломер, для определения длины и углов сторон фигур. После измерения сторон с помощью этих инструментов можно сравнить их между собой и подтвердить или опровергнуть равенство сторон.
Доказательство равенства сторон
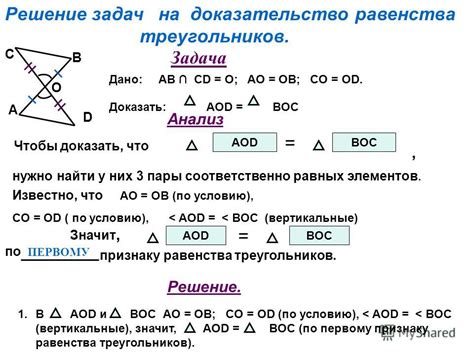
Согласно свойству равенства треугольников, если у двух треугольников все соответствующие стороны и углы равны, то эти треугольники равны. Используя это свойство, можно доказать равенство сторон в различных геометрических фигурах.
Допустим, у нас есть два треугольника ABC и DEF, и необходимо доказать, что сторона AB равна стороне DE. Для этого необходимо проверить, что соответствующие стороны этих треугольников равны. Например, если сторона AB равна стороне DE, а сторона BC равна стороне EF, то можно заключить, что треугольники ABC и DEF равны, и стороны AB и DE равны.
Кроме применения свойств равенства треугольников, также можно использовать другие методы доказательства равенства сторон. Например, метод подобия треугольников, метод углового смежного треугольника, метод равенства противоположных сторон и т.д. Каждый из этих методов имеет свои особенности и используется в зависимости от конкретной задачи.
Доказательство равенства сторон является одним из основных шагов при решении задач по геометрии. После доказательства равенства сторон можно приступить к решению задачи, используя полученное равенство в дальнейших вычислениях или преобразованиях.
Методы подсчета длин сторон
1. Использование известных длин сторон:
Если вам известны длины некоторых сторон фигуры, вы можете использовать их для определения длины остальных сторон. Например, если вы знаете длины двух сторон треугольника, вы можете использовать теорему Пифагора для вычисления длины третьей стороны.
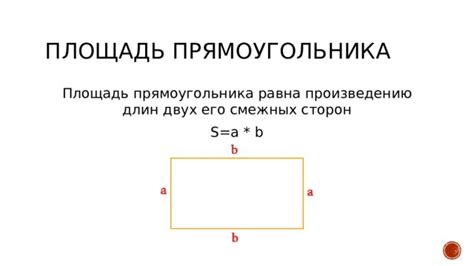
2. Применение свойств фигур:
Каждая фигура имеет свои уникальные свойства, которые можно использовать для определения длин сторон. Например, в прямоугольнике все стороны параллельны и перпендикулярны друг другу.
3. Использование геометрических построений:
Геометрические построения могут помочь в определении длин сторон фигуры. Например, если вам даны две точки на прямой, вы можете провести отрезок между ними с помощью линейки и измерить его длину.
При использовании данных методов необходимо аккуратно и точно работать с известными данными, а также правильно применять геометрические законы и теоремы.
Использование геометрических построений

Один из основных методов геометрических построений – построение перпендикуляра. Для этого нужно использовать циркуль и линейку. Построение перпендикуляра позволяет доказать параллельность двух отрезков или сторон.
Еще одним полезным геометрическим построением является построение равных отрезков. Для этого нужно использовать циркуль и линейку. Построение равных отрезков позволяет доказать равенство сторон или отрезков в геометрических фигурах.
Для создания геометрических построений важно следовать определенным правилам и использовать правильные шаги. При этом нужно быть внимательным и точным, чтобы получить правильные результаты.
Доказательство параллельности сторон

Один из способов доказательства параллельности сторон - это использование соответствующих углов. Если углы между прямыми, которые образуют данные стороны, равны, то можно заключить, что стороны параллельны.
Также можно использовать теорему о параллельных линиях, которая гласит, что если две прямые пересекают третью прямую так, что сумма внутренних углов на одной стороне равна 180 градусам, то эти две прямые параллельны.
Важно отметить, что при доказательстве параллельности сторон необходимо использовать все доступные в задаче факты и свойства геометрии. Кроме того, применение построений, измерений и анализа может помочь в получении дополнительных доказательств.
В общем, доказательство параллельности сторон требует логического мышления и хорошего знания геометрии. Важно быть внимательным к деталям и точно применять нужные методы и теоремы для достижения нужного результата.
Использование свойств углов
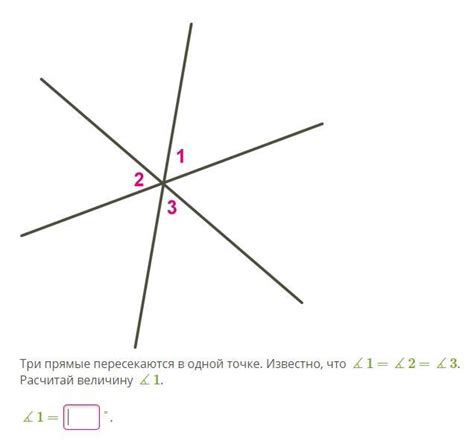
В геометрии существуют определенные свойства углов, которые можно использовать для доказательства равенства и параллельности сторон. Рассмотрим некоторые из них:
- Углы, оборотные друг к другу, равны. Если две стороны пересекаются и образуют смежные углы, то сумма этих углов равна 180 градусам.
- В вертикальных углах стороны параллельны. Если две стороны пересекаются и образуют вертикальные углы, то эти стороны параллельны между собой.
- В прилежащих углах стороны образуют продолжение друг друга. Если две стороны пересекаются и образуют прилежащие углы, то они образуют продолжение друг друга.
- Углы, смежные с одним из вертикальных углов, равны. Если две стороны пересекаются и образуют углы, смежные с вертикальными углами, то эти углы равны между собой.
- Углы, смежные с одним из прилежащих углов, сумма которых равна 180 градусам, равны. Если две стороны пересекаются и образуют углы, смежные с прилежащим углом, и сумма этих углов равна 180 градусам, то эти углы равны между собой.
Методы сравнения длин отрезков
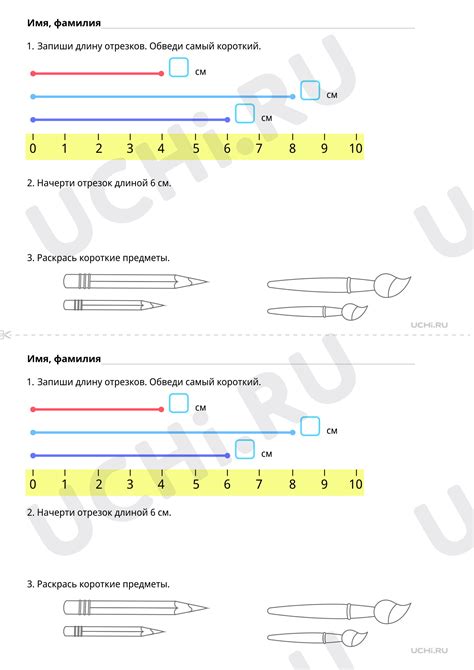
2. Использование геометрических построений. Сравнение длин отрезков можно осуществить путем создания геометрических построений с использованием циркуля и линейки. Например, можно построить квадраты на каждом из отрезков и сравнить их площади. Если площади квадратов будут равны, то длины отрезков также будут равны.
3. Использование таблиц. Для сравнения длин отрезков можно также воспользоваться таблицами. В таблице можно представить координаты концов отрезков, а затем вычислить их длины и сравнить полученные значения. Этот метод особенно удобен при сравнении большого количества отрезков.
4. Использование программных средств. Сравнение длин отрезков можно выполнять с помощью программных средств, таких как САПР (системы автоматизированного проектирования) или математические пакеты вроде MATLAB или Python. Эти инструменты позволяют вычислить длины отрезков и автоматически сравнить их.
Следуя этим методам, можно эффективно сравнить длины отрезков и определить их равенство или неравенство. При этом необходимо учитывать возможные круглые ошибки при вычислениях и использовать соответствующие методы округления значений.



