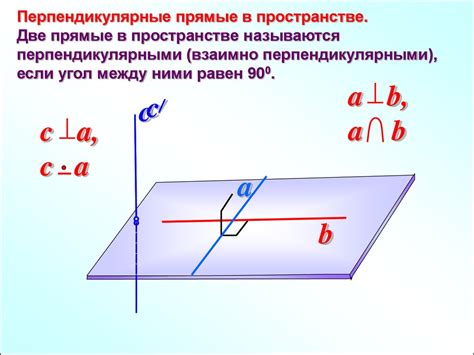
Перпендикулярность - это одно из важных свойств геометрических фигур и объектов. Перпендикулярные линии пересекаются под прямым углом, образуя особый тип геометрических фигур. В призме также можно доказать перпендикулярность прямых, и это доказательство может быть полезным для решения различных геометрических задач.
Призма - это трехмерная геометрическая фигура, которая состоит из двух равных и параллельных многоугольников, называемых основаниями, и боковых граней, которые соединяют соответствующие точки оснований. В призме также присутствуют ребра и вершины, которые являются важными элементами структуры этой фигуры.
Для доказательства перпендикулярности прямых в призме необходимо использовать особое свойство этой фигуры. Основания призмы являются равными и параллельными многоугольниками, поэтому боковые грани имеют одинаковую высоту, а также расположены вдоль прямой, перпендикулярной основанию призмы. Это означает, что боковые грани будут перпендикулярны основанию и другим боковым граням.
Перпендикулярность прямых в призме
Для того чтобы доказать перпендикулярность прямых в призме, можно использовать несколько методов. Один из них основан на свойствах призмы как трехмерной геометрической фигуры:
- Выберем две прямые, которые предположительно могут быть перпендикулярными.
- Найдем две пары смежных граней призмы, составленных из этих прямых. Обозначим их как ABDC и AEFC.
- Если AEFC является прямоугольником и одна из его диагоналей AC пересекается с прямой ABDC под прямым углом, то прямые AB и DC перпендикулярны.
- Если то же самое справедливо и для диагонали CE, то прямые AE и BC также являются перпендикулярными.
Другим способом доказательства перпендикулярности прямых в призме является использование аналитической геометрии:
- Представим прямые в призме в виде уравнений прямых в пространстве. Например, первая прямая может быть задана уравнением l1: x = a1 + t⋅u1, y = b1 + t⋅v1, z = c1 + t⋅w1, где (a1, b1, c1) - произвольная точка на прямой, (u1, v1, w1) - направляющий вектор прямой, t - параметр.
- Аналогично, зададим уравнение второй прямой l2: x = a2 + s⋅u2, y = b2 + s⋅v2, z = c2 + s⋅w2.
- Для доказательства перпендикулярности прямых в призме нужно убедиться, что скалярное произведение векторов направляющих прямых равно нулю:
u1⋅u2 + v1⋅v2 + w1⋅w2 = 0.
Если полученное равенство выполняется, то прямые перпендикулярны друг другу.
Определение перпендикулярности
- Выберите две прямые, которые предположительно могут быть перпендикулярными.
- Постройте плоскости, содержащие эти прямые. Для этого проведите по две отрезка, образующих эти прямые, на каждую сторону от них.
- С помощью угломера, линейки или других измерительных инструментов измерьте угол между плоскостями, содержащими прямые.
- Повторите эти шаги для других предположительно перпендикулярных прямых в призме, чтобы удостовериться в их перпендикулярности.
Помните, что доказательство перпендикулярности прямых в призме требует аккуратного измерения углов и точного построения плоскостей. Ошибки в измерениях или построениях могут привести к неточным или неправильным результатам.
| Пример: | Призма ABCDEFGH с прямыми AB и FG |
| Шаг 1: | Выберите прямые AB и FG |
| Шаг 2: | Постройте плоскости, содержащие AB и FG |
| Шаг 3: | Измерьте угол между плоскостями |
| Шаг 4: | Если угол равен 90 градусам, прямые AB и FG перпендикулярны |
Структура призмы
Основания призмы могут быть различной формы, например, многоугольником или окружностью. Боковые грани призмы представляют собой прямоугольные треугольники, которые соединяют вершины оснований.
Помимо оснований и боковых граней, в призме также присутствуют ребра и вершины. Ребра призмы соединяют соответствующие вершины, а вершины представляют собой точки пересечения ребер призмы.
Чтобы лучше понять структуру призмы, можно использовать таблицу, в которой будут указаны основные характеристики и элементы призмы:
| Элемент | Описание |
|---|---|
| Основания | Две параллельные плоскости, образующие призму. |
| Боковые грани | Прямоугольные треугольники, соединяющие вершины оснований. |
| Ребра | Отрезки, соединяющие соответствующие вершины призмы. |
| Вершины | Точки пересечения ребер призмы. |
| Высота призмы | Отношение высоты призмы к длине ее основания. |
Изучение структуры призмы позволяет лучше понять ее свойства и особенности, а также применять полученные знания при решении задач по геометрии.
Методы доказательства перпендикулярности

1. С помощью допущений в геометрии:
Метод доказательства перпендикулярности основан на аксиомах и постулатах геометрии, которые определены без доказательства. Один из самых простых способов доказательства - это использование аксиомы о перпендикулярности прямых. Если две прямые перпендикулярны к одной и той же прямой, то они перпендикулярны друг другу.
2. С помощью свойств прямых углов:
Если две прямые имеют по одному общему точке и углы, соседствующие с этими прямыми, являются прямыми углами, то прямые перпендикулярны. Для доказательства перпендикулярности можно использовать теорему о сумме углов в треугольнике, если треугольник образован двумя перпендикулярными прямыми и еще одной прямой.
3. С помощью пересечения:
Если две прямые пересекаются и образуют две пары вертикальных углов, то прямые перпендикулярны друг другу. Для доказательства можно использовать принципы вертикальных углов и параллельности, используя определение перпендикулярности и противоположности углов.
Заметим, что вышеуказанные методы доказательства применяются не только для перпендикулярных прямых в призме, но и для перпендикулярных прямых в общем случае.
Примеры решения

Для доказательства перпендикулярности прямых в призме, можно использовать различные методы и свойства геометрии. Вот несколько примеров решений:
1. Доказательство с использованием свойств прямых и плоскостей.
Пусть AB и CD - две прямые в призме, и они должны быть перпендикулярными. Для этого можно воспользоваться следующими шагами:
- Предположим, что прямые AB и CD не перпендикулярны.
- Пусть M - точка пересечения прямых AB и CD.
- Поскольку AB и CD не перпендикулярны, то существует плоскость, проходящая через эти прямые и не пересекающая их перпендикулярно.
- Плоскость, проходящая через прямые AB и CD, также проходит через точку M.
- Таким образом, прямые AB и CD должны быть пересекающимися в точке M, что противоречит начальному предположению.
- Следовательно, прямые AB и CD должны быть перпендикулярными.
2. Доказательство с использованием свойства прямых в призме.
Другой способ доказать перпендикулярность прямых в призме - использовать свойство прямых, проходящих через боковые грани призмы.
- Пусть AB и BC - две прямые в призме, и они должны быть перпендикулярными.
- Предположим, что прямые AB и BC не перпендикулярны.
- Пусть P - точка на прямой AB, лежащая на боковой грани призмы.
- Пусть Q - точка на прямой BC, лежащая на боковой грани призмы.
- Так как прямые AB и BC не перпендикулярны, они должны пересекаться в некоторой точке R.
- Таким образом, точки P, Q и R лежат на одной плоскости, проходящей через боковую грань призмы.
- Но это противоречит свойству прямых, проходящих через боковые грани призмы: они должны быть параллельными.
- Следовательно, прямые AB и BC должны быть перпендикулярными.
Таким образом, с помощью различных методов и свойств геометрии можно доказать перпендикулярность прямых в призме.



