Треугольник ABC – это одна из базовых фигур геометрии, изучаемых с школьных лет. Эта геометрическая фигура состоит из трех отрезков, называемых сторонами, и трех углов, образованных при пересечении этих сторон. Треугольники встречаются повсюду: они образуют строительные конструкции, играют важную роль в тригонометрии и находят применение в различных научных и технических областях. Изучение свойств треугольников имеет большое значение для понимания многих физических и математических явлений.
Один из важных аспектов изучения треугольников – это их напряженные вопросы. Существует множество свойств треугольника, которые могут быть использованы для решения различных задач. Например, известно, что сумма углов треугольника равна 180 градусам. Это свойство позволяет решать задачи на нахождение неизвестных углов треугольника, либо находить значения сторон треугольника, зная значения углов. Это всего лишь одно из множества свойств, которые можно использовать для решения задач на треугольники.
Следует также отметить, что треугольники могут быть различными по типу и размеру. Треугольники делятся на прямоугольные, остроугольные и тупоугольные, а также на равносторонние, равнобедренные и разносторонние. Каждый тип треугольника имеет свои особенности и свойства. Они могут иметь разную форму и размеры, но все они имеют общие свойства, которые могут быть использованы для решения задач на треугольники в различных областях знания, начиная от физики и заканчивая астрономией.
Известные свойства треугольника ABC
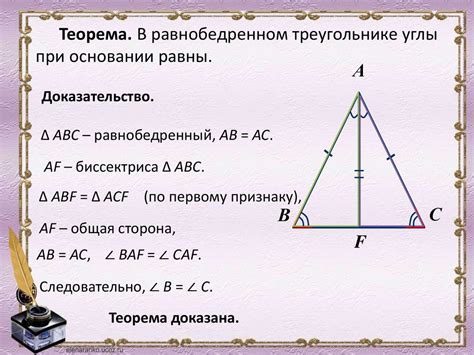
Свойство 1: В треугольнике ABC сумма всех трёх углов равна 180 градусам.
Свойство 2: Сторона AB может быть меньше или равной сумме сторон BC и AC.
Свойство 3: Треугольник ABC может быть разделен на два или более треугольников путем проведения одной или нескольких прямых внутри треугольника.
Свойство 4: Сумма длин двух сторон треугольника всегда больше, чем длина третьей стороны.
Свойство 5: Треугольник ABC может быть классифицирован по длинам сторон и значениям углов. Например, треугольник может быть равносторонним, равнобедренным или разносторонним.
Эти свойства треугольника ABC представляют собой лишь часть его характеристик и могут быть использованы в различных задачах геометрии и физики.
Геометрические свойства треугольника ABC
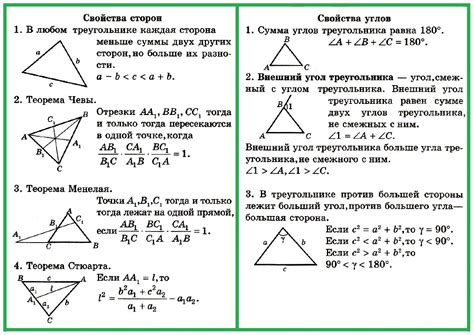
Некоторые известные свойства треугольника ABC:
- Углы треугольника: треугольник ABC имеет три угла - угол A, угол B и угол C.
- Сумма углов: внутренние углы треугольника ABC всегда суммируются до 180 градусов.
- Стороны треугольника: стороны треугольника ABC обозначаются как отрезки AB, BC и AC.
- Высоты: треугольник ABC имеет три высоты - высоту, опущенную из вершины A на основание BC, высоту, опущенную из вершины B на основание AC, и высоту, опущенную из вершины C на основание AB.
- Медианы: треугольник ABC имеет три медианы - медиану, проведенную из вершины A к середине стороны BC, медиану, проведенную из вершины B к середине стороны AC, и медиану, проведенную из вершины C к середине стороны AB.
- Биссектрисы: треугольник ABC имеет три биссектрисы - биссектрису угла A, биссектрису угла B и биссектрису угла C. Биссектриса угла делит соответствующий угол на два равных угла.
- Радиусы вписанной и описанной окружностей: треугольник ABC можно описать вокруг окружности и вписать внутрь окружности. Радиус окружности, описанной вокруг треугольника, называется описанным радиусом и обозначается R. Радиус окружности, вписанной в треугольник, называется вписанным радиусом и обозначается r.
Изучение геометрических свойств треугольника ABC помогает в решении различных задач и задач построения, а также в понимании более сложных математических концепций.
Определение и основные понятия

В треугольнике существуют следующие основные понятия:
- Стороны треугольника: это отрезки, соединяющие вершины треугольника.
- Вершины треугольника: это точки, в которых пересекаются стороны треугольника.
- Углы треугольника: это пространственные фигуры, образованные двумя сторонами треугольника.
- Высота треугольника: это отрезок, соединяющий вершину треугольника с противоположной стороной и перпендикулярный этой стороне.
- Медианы треугольника: это отрезки, соединяющие каждую вершину треугольника с серединой противоположной стороны.
- Биссектрисы треугольника: это отрезки, делящие каждый угол треугольника на две равные части.
- Вписанный угол: это угол, вершина которого лежит на окружности, вписанной в треугольник, а стороны проходят через вершины треугольника.
Понимание этих основных понятий является фундаментом для изучения и понимания свойств и отношений в треугольниках.
Соотношения между сторонами и углами
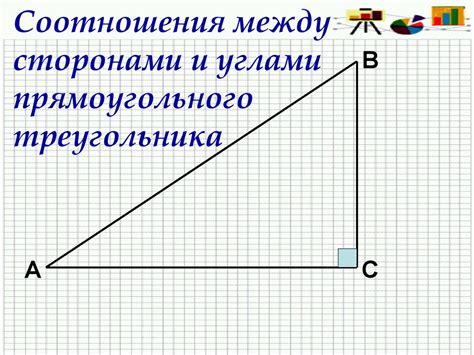
Треугольник ABC имеет несколько важных соотношений между своими сторонами и углами:
1. Теорема синусов: в любом треугольнике отношение длин сторон к синусам противолежащих им углов одинаково. Таким образом, для треугольника ABC с углами A, B и C и сторонами a, b и c соответственно, справедлива формула:
a / sin(A) = b / sin(B) = c / sin(C)
2. Теорема косинусов: углы треугольника и длины его сторон связаны с помощью косинусов. Для треугольника ABC со сторонами a, b, c и углами A, B, C соответственно, справедлива формула:
c^2 = a^2 + b^2 - 2ab * cos(C)
и аналогичные формулы для сторон a и b.
3. Теорема о сумме углов треугольника: сумма углов треугольника всегда равна 180 градусам. Таким образом, для треугольника ABC с углами A, B и C, справедливо:
A + B + C = 180°
Эти соотношения помогают в решении различных задач, связанных с треугольником ABC.
Треугольник ABC в теории вероятности
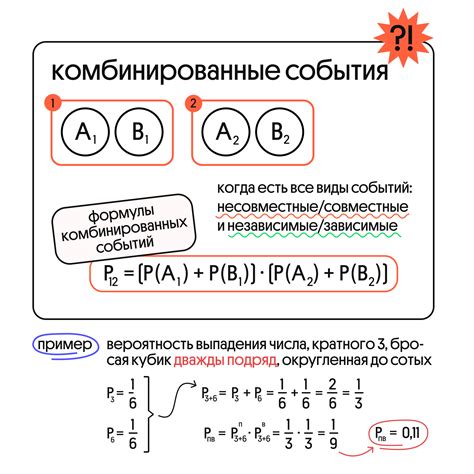
В теории вероятности треугольник ABC может быть использован для моделирования различных случайных событий. Свойства треугольника ABC могут быть использованы для вычисления вероятностей и решения различных задач.
Некоторые из известных свойств треугольника ABC могут быть полезными в теории вероятности, такие как:
- Сумма углов треугольника равна 180 градусам. Это свойство может быть использовано для вычисления вероятности наступления событий, связанных с углами треугольника.
- Соотношение между сторонами треугольника ABC может быть использовано для вычисления вероятностей, связанных с длинами отрезков.
- Теорема Пифагора может быть применена для вычисления вероятностей, связанных с гипотенузой треугольника ABC.
Эти свойства могут быть использованы для построения моделей, вычисления вероятностей и решения различных задач в теории вероятности.
Вероятность появления заданного треугольника
Вероятность появления заданного треугольника может быть рассчитана на основе известных свойств треугольника ABC. Для этого необходимо учесть следующие факторы:
| Свойство треугольника | Влияние на вероятность |
|---|---|
| Длины сторон треугольника | Чем длины сторон ближе к заданным значениям, тем выше вероятность появления заданного треугольника. |
| Углы треугольника | Чем углы треугольника ближе к заданным значениям, тем выше вероятность появления заданного треугольника. |
| Площадь треугольника | Чем площадь треугольника ближе к заданному значению, тем выше вероятность появления заданного треугольника. |
| Тип треугольника (остроугольный, тупоугольный, прямоугольный) | В зависимости от типа треугольника вероятность может быть различной. Некоторые типы треугольников могут иметь более высокую вероятность появления. |
Для расчета вероятности необходимо учесть все указанные свойства и применить соответствующие формулы. Однако, точные значения вероятности появления заданного треугольника могут быть сложны для вычисления. В данном случае, более реалистичным подходом может быть сравнение вероятностей появления различных треугольников на основе известных свойств.



