Расчет параметров геометрических фигур является важным этапом при решении различных задач в науке и технике. Конус – одна из наиболее распространенных фигур, которая часто используется в промышленности, архитектуре и других отраслях деятельности. Для определения объема и площади поверхности конуса часто требуется знать его осевое сечение.
Осевое сечение конуса – это плоская фигура, которую можно получить путем пересечения конуса плоскостью, параллельной его основанию. Длина сторон осевого сечения является ключевым параметром, поскольку она определяет форму и размеры осевого сечения конуса.
Существует несколько методов расчета длины сторон осевого сечения конуса. Один из самых распространенных методов основан на использовании подобия треугольников. При данном методе известны длины сторон основания и высота конуса. С помощью подобия треугольников можно вычислить длины сторон осевого сечения, используя пропорциональность сторон.
Определение длины сторон осевого сечения конуса
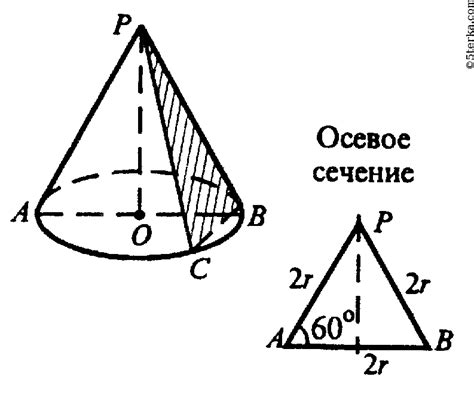
Существует несколько методов расчета длины сторон осевого сечения конуса, но один из наиболее использованных - это использование тригонометрии и формулы для расчета длины окружности.
Для начала определяется радиус осевого сечения конуса, который является расстоянием от вершины конуса до точки сечения по прямой, проходящей через ось конуса. После нахождения радиуса, можно применить формулу для расчета длины окружности:
Длина окружности = 2 * π * радиус
Где π (пи) - это математическая константа, приблизительно равная 3.14159.
Таким образом, по известной длине осевого сечения конуса и формуле для расчета длины окружности, мы можем определить длину сторон осевого сечения конуса.
| Известная длина сторон осевого сечения конуса | Длина окружности |
|---|---|
| 5 см | 10π см |
| 10 см | 20π см |
| 15 см | 30π см |
Таким образом, для конуса с известной длиной сторон осевого сечения 5 см, длина окружности будет 10π см.
Понятие и значение
Длина сторон осевого сечения имеет важное значение при расчете некоторых параметров и свойств конуса. Например, зная длину стороны осевого сечения, можно вычислить площадь этого сечения, объем конуса, а также найти высоту и радиус основания конуса.
При работе с конусами важно правильно понимать и использовать понятие осевого сечения и знать методы расчета его длины. Это поможет более точно определить форму и размеры конуса, а также решить задачи, связанные с его применением в науке, технике и других областях. Важно иметь представление о том, как поведут себя свойства и параметры конуса при изменении длины сторон осевого сечения.
Геометрическое описание сечения
В зависимости от положения плоскости относительно вершины конуса, сечение может быть окружностью, эллипсом, параболой или гиперболой.
Окружность – это сечение конуса плоскостью, параллельной основанию. Радиус окружности в осевом сечении конуса будет равен радиусу основания конуса.
Эллипс – это сечение конуса плоскостью, не параллельной основанию и не проходящей через вершину конуса. Эллипс в осевом сечении конуса будет иметь форму эллипсоида.
Парабола – это сечение конуса плоскостью, параллельной одной из боковых граней и проходящей через вершину конуса. Парабола в осевом сечении конуса будет иметь форму параболоида.
Гипербола – это сечение конуса плоскостью, пересекающей оба листа поверхности конуса. Гипербола в осевом сечении конуса будет иметь форму гиперболоида.
Способы расчета длины сторон
Для расчета длины сторон осевого сечения конуса с известной длиной, существуют несколько методов:
1. Использование формулы для расчета длины окружности:
| Формула | Расчет |
|---|---|
| Длина окружности | Л = 2πr |
| Длина стороны осевого сечения | длина осевого сечения = Длина окружности |
2. Использование теоремы Пифагора для расчета длины сторон осевого сечения прямоугольного треугольника. В данном случае, длина стороны осевого сечения будет равна гипотенузе треугольника.
| Формула | Расчет |
|---|---|
| Теорема Пифагора | a^2 + b^2 = c^2 |
| Длина стороны осевого сечения | длина осевого сечения = √(a^2 + b^2) |
3. Использование тригонометрических функций для расчета длины сторон осевого сечения в случае, если известны углы и длины других сторон треугольника.
При выборе способа расчета, необходимо учитывать доступные данные и требования задачи, чтобы получить точные результаты.
Примеры расчета длины сторон
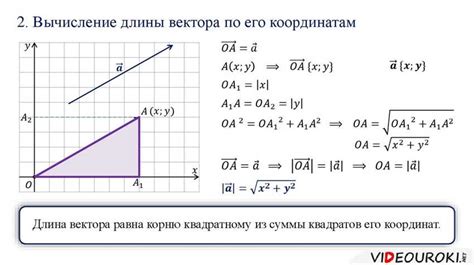
Пример 1:
Для конуса с радиусом основания 5 см и высотой 10 см, найдем длину боковой стороны.
Используя теорему Пифагора, найдем длину образующей конуса:
l = √(r² + h²) = √(5² + 10²) = √(25 + 100) = √125 ≈ 11.18 см
Таким образом, длина боковой стороны осевого сечения этого конуса составляет приблизительно 11.18 см.
Пример 2:
Рассмотрим конус с радиусом основания 8 см и высотой 15 см. Найдем длину основания этого конуса.
Используя формулу для длины окружности, найдем длину окружности основания:
C = 2πr = 2π × 8 = 16π ≈ 50.27 см
Таким образом, длина основания осевого сечения этого конуса составляет приблизительно 50.27 см.



