Десятичная дробь - это числовая величина, состоящая из целой части и дробной части, разделенных точкой. Насколько точной будет десятичная дробь, зависит от количества десятичных знаков, которые мы используем для ее записи. Например, если у нас есть число 3.14, то целая часть равна 3, а дробная - 14. В данном случае дробная часть содержит два десятичных знака.
Представление десятичной дроби имеет свои особенности. Одна из них - наличие бесконечного количества десятичных знаков после запятой при представлении некоторых чисел. Например, число пи (π) является бесконечной десятичной дробью. Его представление начинается с 3.141592653589793238 и не имеет окончания.
Для удобства чтения и записи десятичных дробей часто используется знак препинания - запятая. Однако, в некоторых странах, включая США, принято использовать точку вместо запятой в качестве разделителя между целой и дробной частями числа. Это может привести к некорректному представлению числа, если при чтении его использовать другой стандарт.
Представление десятичной дроби:

Для удобства чтения и записи десятичных дробей используется десятичная система счисления, которая основана на использовании десяти цифр: от 0 до 9. Каждый десятичный разряд в дроби имеет свое значение, зависящее от его позиции в числе. Например, в числе 123.456 сотые и десятые это цифры 4 и 5, соответственно.
Для записи десятичных дробей в удобной форме используется таблица. В данной таблице целая часть числа записывается слева от разделительного символа (запятой или точки), а десятичная часть записывается справа от разделительного символа. В каждой позиции таблицы указывается значение цифры в соответствующем разряде.
| Сотые | Десятые | Единицы | Десятки | Сотни |
|---|---|---|---|---|
| 4 | 5 | 3 | 2 | 1 |
Таким образом, представление десятичной дроби позволяет наглядно и понятно записывать и интерпретировать дробные значения в различных контекстах, например, в науке, финансах или ежедневной жизни.
Определение и основные понятия:

В десятичной дроби целая часть представляет количество целых единиц, а дробная часть показывает количество долей целой единицы. Дробная часть записывается после запятой и состоит из чисел от 0 до 9.
Каждая цифра дробной части десятичной дроби имеет свое значение, которое зависит от ее позиции относительно запятой. Например, в числе 0,25 цифра 2 стоит в позиции десятых, а цифра 5 - в позиции сотых долей.
Десятичная дробь может быть конечной или бесконечной. В случае конечной десятичной дроби, дробь имеет конечное число десятичных разрядов после запятой. В случае бесконечной десятичной дроби, дробь имеет бесконечное число десятичных разрядов или повторяющийся цикл чисел.
Для удобства чтения и записи более длинных десятичных дробей, используются специальные обозначения, такие как знак "..." или символы многоточия. Например, число Пи может быть записано как 3,14159...
Показательная форма:

Например, десятичная дробь 0.001 может быть представлена в показательной форме как 1 * 10^(-3), где основание равно 10, а показатель степени равен -3. Это означает, что запятая сдвигается три разряда влево.
Показательная форма особенно полезна для работы с очень малыми или очень большими числами, так как позволяет упростить запись чисел с большим количеством нулей или цифр.
Например, число 250 000 000 может быть записано в показательной форме как 2.5 * 10^8, что делает его более компактным.
Показательная форма также используется при научных вычислениях, в физике, химии и других науках, где требуется работа с очень малыми или очень большими числами.
Бесконечная десятичная дробь:

Запись бесконечных десятичных дробей зачастую требует использования округления или приближения для удобства использования и представления числа. Например, число "e" (основание натурального логарифма) равно примерно 2.71828..., но для удобства записи и использования в математических формулах часто округляется до 2.718.
Бесконечные десятичные дроби широко используются в науке, физике, математике, статистике и других областях, где точность и приближение имеют значение. Они являются неотъемлемой частью работы с великими числами, а также использования представления чисел с большой точностью.
Повторяющиеся десятичные дроби:

Повторяющимися десятичными дробями называются числа, в которых после запятой в десятичной записи одна или несколько цифр повторяются бесконечно. Они представляются в виде одного или нескольких периодов, которые повторяются в бесконечности.
Например, десятичная дробь 0,12121212... имеет период 12, а дробь 0,7777777... - период 7. Такие числа обычно записывают с помощью символа повторения над периодом, например 0,12̅ и 0,7̅, чтобы обозначить бесконечное повторение.
Повторяющиеся десятичные дроби можно представить с помощью обыкновенных дробей. Для этого нужно обозначить период числителем и знаменателем, состоящими из цифр этого периода. Например, дробь 0,12121212... можно представить как 12/99, а дробь 0,7777777... - как 7/9.
Повторяющиеся десятичные дроби важны, так как они используются в разных математических и научных расчетах. Изучение их свойств позволяет понять особенности и закономерности, которые проявляются при работе с такими числами.
Периодическая десятичная дробь:
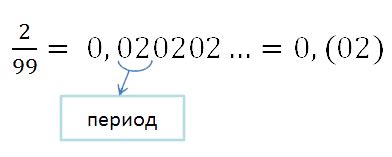
Периодическая десятичная дробь может быть конечной или бесконечной. Конечная периодическая дробь имеет конечное количество цифр в периоде, тогда как бесконечная периодическая дробь имеет бесконечное количество цифр в периоде.
Примеры конечных периодических десятичных дробей: 0.3333333... (1/3), 0.6666666... (2/3).
Примеры бесконечных периодических десятичных дробей: 0.142857142857... (1/7), 0.12121212... (12/99).
Для представления периодической десятичной дроби в числовом виде можно использовать знания о периодах и их повторяемости. Существуют также специальные алгоритмы для преобразования периодической десятичной дроби в рациональную дробь.
Конечная десятичная дробь:
Например, десятичная дробь 0,25 является конечной, так как после запятой идут только два знака. Она может быть записана в десятичной форме без приближения или округления: 0,25.
Другим примером конечной десятичной дроби может быть 1,75. В этом случае после запятой идут два знака, и дробь может быть представлена в десятичной форме без потери точности.
Основное свойство конечной десятичной дроби состоит в том, что она может быть записана в виде рационального числа, то есть в виде дроби, где числитель и знаменатель - целые числа.
Если в десятичной дроби после запятой идут бесконечно повторяющиеся знаки (например, 0,333...), то такая дробь называется периодической. Однако, если в десятичной дроби после запятой идут только конечное количество повторяющихся знаков (например, 0,5353), то такая дробь также является конечной десятичной дробью.
Конечные десятичные дроби широко используются в реальной жизни для представления точных значений в различных областях, таких как финансы, наука и инженерия.



