Введение

Графы - одна из наиболее важных абстрактных структур данных в информатике и математике. Они широко применяются для моделирования и анализа сложных систем, таких как социальные сети, транспортные сети или сети связи. В данной статье мы рассмотрим различные виды графов и дадим определение каждого из них.
Ориентированный граф
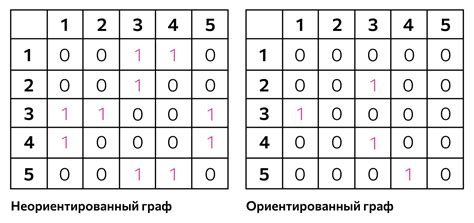
Ориентированный граф - это граф, в котором каждое ребро имеет направление. Это означает, что ребро соединяет одну вершину (начальную) с другой (конечной). Направление ребра можно представить как стрелку, указывающую от начальной к конечной вершине. Ориентированный граф может использоваться для моделирования направленных отношений или потоков данных.
Пример:
Допустим, у нас есть ориентированный граф, представляющий транспортные маршруты в городе. Каждая вершина представляет остановку, а ребро указывает наличие маршрута от одной остановки к другой. Направление ребра отражает направление движения по маршруту.
Неориентированный граф
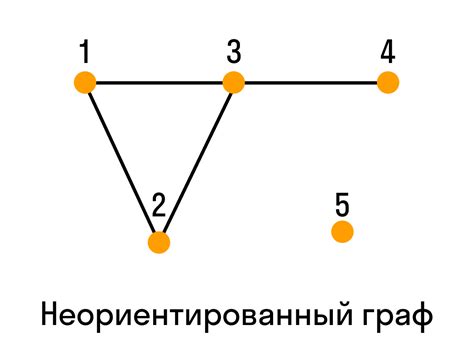
Неориентированный граф - это граф, в котором ребра не имеют направления. Это означает, что связь между двумя вершинами является симметричной, и мы можем перемещаться между ними в обоих направлениях. Неориентированный граф может использоваться для моделирования ненаправленных связей, таких как дружеские отношения или коммуникационные сети.
Пример:
Рассмотрим неориентированный граф, представляющий дружеские связи между людьми в сети социальных контактов. Каждая вершина представляет человека, а ребро указывает наличие дружеской связи между двумя людьми. Дружба является взаимной, поэтому ребра в этом графе не имеют направления.
Взвешенный граф
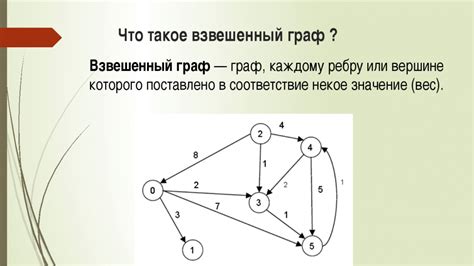
Взвешенный граф - это граф, в котором каждое ребро имеет некоторую числовую характеристику, называемую весом. Веса могут представлять различные характеристики или стоимости, связанные с ребром. Взвешенный граф может использоваться для моделирования различных ситуаций, таких как стоимость перевозки груза или пропускной способности сети.
Пример:
Представим сеть транспортных маршрутов в виде взвешенного графа, где каждое ребро имеет вес, отражающий стоимость поездки по данному маршруту. Например, маршрут с более высокой стоимостью может означать большую длительность пути или наличие платы за проезд.
Заключение

Графы представляют собой мощный инструмент для моделирования и анализа сложных систем. Ориентированные, неориентированные и взвешенные графы предоставляют различные способы представления и работы с данными. Знание основных видов графов и их определений является важным для понимания и применения графовых алгоритмов и структур данных в реальных приложениях.
Определение графа и его приложения
Графы являются универсальным языком для моделирования и анализа различных систем. Они находят широкое применение в различных областях, включая компьютерные науки, телекоммуникации, социальные сети, транспортные сети и многое другое.
Применения графов:
- Анализ социальных сетей: Графы могут быть использованы для анализа связей между людьми в социальных сетях. Это позволяет исследовать структуру и характеристики социальных сетей, а также предсказывать потенциальные связи между людьми.
- Маршрутизация в транспортных сетях: Графы используются для поиска оптимальных маршрутов в транспортных сетях, таких как дороги, авиалинии или железные дороги. Это позволяет улучшить эффективность и экономичность транспортных систем.
- Анализ данных: В области анализа данных графы используются для моделирования сложных отношений и взаимодействий между объектами, такими как пользователи, товары или события. Это помогает выявлять скрытые паттерны и структуры в данных.
- Алгоритмы и искусственный интеллект: Графы являются основой для многих алгоритмов искусственного интеллекта, таких как поиск в глубину, поиск в ширину, алгоритм Дейкстры и алгоритмы кластеризации.
Это лишь некоторые примеры того, как графы применяются в различных областях. Они являются мощным инструментом для моделирования и анализа сложных систем и отношений.



