Квадратичная функция – это функция вида f(x) = ax^2 + bx + c, где a, b и c – это коэффициенты функции, причем коэффициент a не равен нулю. График квадратичной функции является параболой, которая может быть направленной вверх или вниз, в зависимости от знака коэффициента a. Важно понимать, что график квадратичной функции представляет собой важное геометрическое представление ее поведения и характеристик.
График квадратичной функции может раскрывать много полезной информации о функции. Во-первых, его форма может указывать на то, каково направление открытия параболы. Если коэффициент a положительный, то парабола открывается вверх, а если отрицательный, то вниз. Это может иметь важные последствия для поиска экстремумов функции или решения уравнений. Во-вторых, график также может показать вершину параболы, которая является экстремальной точкой функции. Вершина имеет координаты (h, k), где h и k можно найти с использованием формул: h = -b/2a и k = f(h).
Кроме того, график квадратичной функции может также показать оси симметрии, прямую, перпендикулярную оси OX в точке вершины параболы. Отражение параболы относительно оси симметрии может помочь определить ее дополнительные характеристики, такие как наличие симметричных корней или боковых точек разворота. Важно изучить график квадратичной функции, чтобы более глубоко понять ее свойства, поведение и решение уравнений, а также использовать его для представления данных и анализа.
Что показывает график квадратичной функции?
График квадратичной функции представляет собой кривую, которая показывает зависимость изменения значений функции от значения независимой переменной. График квадратичной функции имеет форму параболы, которая может быть направленной вверх или вниз.
Парабола графика квадратичной функции может иметь различное положение относительно оси абсцисс и оси ординат. Если парабола направлена вверх, то это означает, что функция имеет минимум, который является наименьшим значением функции. Если парабола направлена вниз, то функция имеет максимум, который является наибольшим значением функции.
График квадратичной функции также может иметь вершину, которая представляет точку на параболе, где она достигает своего минимума или максимума. Вершина параболы может быть определена с помощью формулы, которая зависит от коэффициентов квадратичной функции.
Кроме того, график квадратичной функции может также показывать особые точки, такие как точки пересечения параболы с осями абсцисс и ординат, а также точки экстремума функции.
Изучение графика квадратичной функции позволяет понять, как функция меняется в зависимости от значения независимой переменной, и помогает решать различные задачи, такие как нахождение точек экстремума или решение уравнений.
Математика уровень средней школы

Одной из важных тем математики уровня средней школы является изучение графиков квадратичных функций. График квадратичной функции представляет собой параболу, которая может иметь различные формы и положение на координатной плоскости.
Квадратичная функция задается уравнением вида y = ax^2 + bx + c, где a, b и c - коэффициенты, определяющие форму и положение параболы. График квадратичной функции состоит из точек, удовлетворяющих уравнению функции.
Изучение графиков квадратичных функций позволяет анализировать особенности их поведения. Например, по графику можно определить вершину параболы, направление ее выпуклости, а также наличие или отсутствие корней функции.
График квадратичной функции может иметь различные формы. В зависимости от значений коэффициентов a, b и c парабола может быть направлена вверх или вниз, смещена влево или вправо, сужена или растянута. Исследование графика квадратичной функции и определение ее особых точек позволяет получить полное представление о ее форме и поведении в различных областях определения.
Изучение графиков квадратичных функций не только развивает навыки работы с координатной плоскостью и алгебраическими выражениями, но и позволяет увидеть практическое значение математики в реальной жизни. Квадратичные функции широко применяются в физике, экономике, инженерии и других областях науки и техники.
Таким образом, изучение графиков квадратичных функций является важным компонентом математики уровня средней школы и создает прочную основу для дальнейшего изучения математики в высшей школе и вузе.
Как изображается график квадратичной функции
Для изображения графика квадратичной функции необходимо выбрать некоторое количество значений переменной (x) и рассчитать соответствующие им значения функции (y). Затем эти точки могут быть отмечены на координатной плоскости и соединены кривой линией.
График квадратичной функции может иметь различную форму, в зависимости от значений коэффициентов a, b и c. Например, если коэффициент a положителен, график будет иметь форму параболы, направленной вверх. Если a отрицателен, график будет направлен вниз. Коэффициенты b и c также влияют на форму и положение графика.
Особенности графика квадратичной функции также могут быть определены с помощью дискриминанта, который является выражением подкоренного выражения в формуле для нахождения корней квадратного уравнения. Например, если дискриминант положителен, квадратичная функция имеет два различных вещественных корня, что может отразиться на графике.
Отражение формы графика относительно оси ординат
Квадратичная функция имеет общий вид y = ax^2 + bx + c, где a, b и c - это коэффициенты. Коэффициент a отвечает за форму графика и определяет, будет ли он направлен вниз или вверх. Если a > 0, то график будет направлен вверх, если a < 0, то график будет направлен вниз.
Отражение формы графика относительно оси ординат происходит, когда коэффициент a меньше нуля. При таком положении квадратичной функции, график будет симметричным относительно оси ординат. Это значит, что если на графике есть точка (x, y), то точка (-x, y) тоже будет находиться на графике.
Отражение формы графика относительно оси ординат позволяет наглядно представить симметричность функции, а также упрощает анализ его свойств. Например, если график квадратичной функции имеет вершину в точке (2, 4), то мы можем сразу заключить, что точка (-2, 4) также находится на графике.
Анализ вершины графика
Определение положения вершины графика квадратичной функции осуществляется путем решения системы уравнений:
x = -b/2a
y = -D/4a
где a, b и c - коэффициенты уравнения квадратичной функции, а D - дискриминант.
Анализ вершины графика позволяет определить такие характеристики функции, как:
- Максимум или минимум функции: Если коэффициент a больше нуля, то функция имеет минимум в вершине графика. Если коэффициент a меньше нуля, то функция имеет максимум.
- Значение функции в вершине: Значение y в точке вершины графика показывает, какое значение достигает функция в своем экстремуме.
- Симметричность графика: Вершина графика является осью симметрии. В то же время, сам график симметричен относительно вертикальной прямой, проходящей через вершину.
Анализ вершины графика квадратичной функции позволяет получить важную информацию о ее форме и особенностях. Это помогает лучше понять поведение функции и использовать ее в математических моделях и практических задачах.
Процесс нахождения осей симметрии квадратичной функции
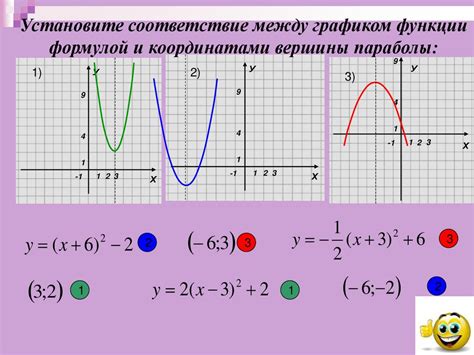
Для нахождения оси симметрии квадратичной функции, необходимо записать функцию в канонической форме: y = a(x - h)^2 + k, где координаты вершины параболы равны (h, k). В данной форме ось симметрии находится в точке x = h.
Процесс нахождения оси симметрии включает следующие шаги:
- Записать квадратичную функцию в канонической форме.
- Найти координаты вершины параболы по формулам h = -b / 2a и k = f(h), где a, b и c - коэффициенты квадратичной функции, а f(x) - функция выражающая значение квадратичной функции для данного значения x.
- Ось симметрии проходит через точку вершины параболы, поэтому x = h.
Процесс нахождения оси симметрии квадратичной функции позволяет легко определить симметричность графика, что в свою очередь помогает в изображении и анализе функции.
Примеры графиков квадратичных функций
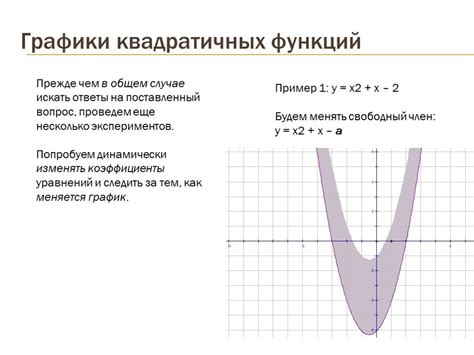
Рассмотрим несколько примеров графиков квадратичных функций:
Пример 1:
Пусть у нас есть функция f(x) = x^2. График этой функции будет параболой, которая открывается вверх и проходит через точку (0,0). Чем больше значение x, тем больше будет значение f(x).
Пример 2:
Рассмотрим функцию f(x) = -2x^2 + 3x + 1. График этой функции тоже будет параболой, но уже с отрицательным коэффициентом a. Такая парабола будет открываться вниз и проходить через точку (0,1).
Пример 3:
Представим функцию f(x) = x^2 - 4. График этой функции будет параболой, смещенной вниз на 4 единицы по оси OY. Он также будет проходить через точку (0,-4).
Это лишь несколько примеров графиков квадратичных функций, их форма и положение зависят от значений коэффициентов a, b и c.



