Прямоугольные треугольники - это фигуры, которые привлекают внимание своей простотой и геометрической гармонией. Они имеют особую структуру, которая предлагает аналитическим решениям широкие возможности. Одной из важных характеристик прямоугольных треугольников является средняя линия, которая играет важную роль в изучении их свойств.
Средняя линия в прямоугольном треугольнике является отрезком, соединяющим середины двух сторон, не являющихся гипотенузой. Таким образом, она делит гипотенузу пополам. Свойства средней линии позволяют провести ряд аналитических рассуждений о прямоугольных треугольниках и использовать их в решении геометрических задач.
Средняя линия играет важную роль в вычислении площади прямоугольного треугольника. Для прямоугольных треугольников площадь можно вычислить по формуле: площадь = половина произведения катетов. Также средняя линия служит для определения медианы и медиатрицы, которые имеют свои особенности и применение в различных задачах.
Роль средней линии в прямоугольных треугольниках
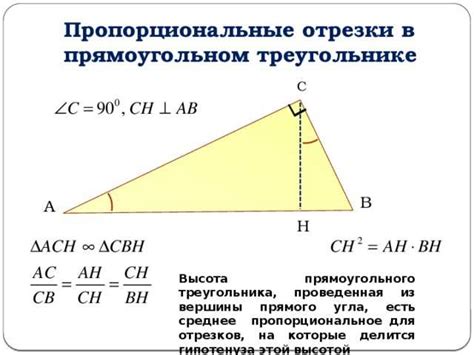
Одной из основных функций средней линии является разделение треугольника на две равные части. Таким образом, средняя линия делит площадь треугольника пополам. Это свойство может быть использовано, например, для вычисления площади треугольника, зная площадь одной из его половин.
Кроме того, средняя линия также является основой для нахождения высоты треугольника. Высотой треугольника называется отрезок, проведенный из вершины прямого угла треугольника к противоположной стороне и перпендикулярный ей. Очевидно, что средняя линия является основой для проведения такого отрезка и позволяет определить его длину.
Также средняя линия относится к теореме Пифагора. Теорема Пифагора утверждает, что квадрат длины гипотенузы прямоугольного треугольника равен сумме квадратов длин катетов. Средняя линия в прямоугольных треугольниках предоставляет дополнительные возможности для проверки этой теоремы путем использования ее длины.
| Признак | Связь с средней линией |
|---|---|
| Равнобедренность | Средняя линия является высотой и медианой |
| Серединный перпендикуляр | Средняя линия равна половине гипотенузы |
| Непосредственное применение теоремы Пифагора | Средняя линия является диагональю прямоугольного треугольника |
Таким образом, средняя линия в прямоугольных треугольниках имеет не только визуальное значение, но и выполняет ряд важных функций, связанных с разделением площади треугольника на равные части, определением высоты треугольника и проверкой теоремы Пифагора.
Функции средней линии в прямоугольных треугольниках
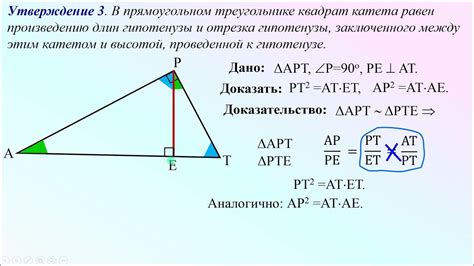
1. Длина средней линии. Чтобы найти длину средней линии, нужно сложить длины двух сторон и разделить полученную сумму на 2. Формула для расчета выглядит следующим образом:
| Длина средней линии | = | (Длина первой стороны + Длина второй стороны) / 2 |
2. Свойства средней линии. В прямоугольном треугольнике средняя линия:
- Проходит через вершину прямого угла.
- Половина длины гипотенузы. Гипотенуза - самая длинная сторона прямоугольного треугольника, и средняя линия является ее половиной.
- Делит треугольник на два треугольника равной площади.
3. Применение в расчетах. Средняя линия в прямоугольных треугольниках может использоваться для нахождения площади. Если известны длины средней линии и одной из сторон треугольника, можно вычислить площадь по формуле:
| Площадь треугольника | = | (Длина средней линии * Длина известной стороны) / 2 |
Также средняя линия в прямоугольных треугольниках может использоваться для нахождения высоты. Высота - это отрезок, проведенный из вершины прямого угла к противоположной стороне треугольника. Длину высоты можно вычислить, зная длину средней линии и длину стороны, к которой проведена высота, по формуле:
| Длина высоты | = | (Длина средней линии * Длина стороны) / Длина гипотенузы |
Функции средней линии в прямоугольных треугольниках имеют практическое применение в различных областях, таких как архитектура, строительство и геометрия.
Связь средней линии с другими элементами треугольника
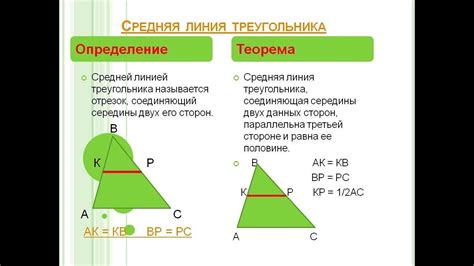
Средняя линия также связана с другими элементами треугольника. Например, она параллельна и имеет длину, равную половине основания треугольника. Это значит, что длина средней линии равна половине длины основания. Также средняя линия делит высоту треугольника на две равные части.
Следовательно, средняя линия является важным инструментом для изучения их свойств и взаимосвязей с другими элементами треугольника. Она предоставляет нам ценную информацию о пропорциях и симметрии треугольника.
| Свойство | Описание |
|---|---|
| Параллельность | Средняя линия параллельна основанию треугольника и одной из боковых сторон |
| Длина | Длина средней линии равна половине длины основания треугольника |
| Разделение | Средняя линия делит высоту треугольника на две равные части |
Изучение связи средней линии с другими элементами треугольника позволяет нам лучше понять его геометрические свойства и использовать их для решения задач и построения геометрических моделей.
Влияние средней линии на свойства треугольника
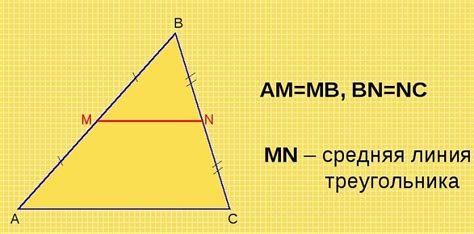
Во-первых, средняя линия делит треугольник на два равных треугольника. Каждый из них имеет равные углы и стороны, что делает их подобными друг другу. Если мы знаем свойства одного из этих треугольников, мы можем вывести свойства второго треугольника с помощью подобия.
Во-вторых, средняя линия является медианой треугольника. Медиана – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Средняя линия делит медиану пополам, а также делит треугольник на две равные по площади части. Кроме того, точка пересечения медиан треугольника называется центром тяжести треугольника. От этой точки до вершин треугольника все медианы равны и пересекаются в одной точке – центре тяжести.
Средняя линия также влияет на длины и площади треугольников. Если длины сторон треугольника равны, то длина средней линии будет равна половине длины стороны треугольника. Поэтому, зная длины сторон треугольника, мы можем найти длину средней линии с помощью простых математических расчетов.
Таким образом, средняя линия является важным элементом треугольника, влияющим на его свойства и характеристики. Изучение средней линии помогает нам лучше понять структуру и особенности треугольника в геометрии.
Применение средней линии в практических задачах

Одно из применений средней линии - нахождение площади треугольника. Площадь треугольника можно выразить через длину его средней линии. Если мы знаем длины обоих сторон треугольника и длину его средней линии, мы можем использовать формулу: площадь треугольника = (длина средней линии * длина боковой стороны) / 2. Это может быть полезным при решении задач, если у нас есть информация о длине средней линии и одной из боковых сторон.
Средняя линия также может быть использована для определения радиуса вписанной окружности в прямоугольный треугольник. Радиус вписанной окружности - это расстояние от центра окружности до любой из сторон треугольника. Если мы знаем длины двух сторон треугольника и длину его средней линии, мы можем использовать формулу: радиус вписанной окружности = (площадь треугольника) / (полупериметр треугольника), где полупериметр треугольника = (длина средней линии + длина двух сторон) / 2. Это может помочь в решении задач, связанных с вписанными окружностями в треугольник.
Еще одним применением средней линии является определение высоты треугольника. Высота треугольника - это перпендикуляр, проведенный от вершины до основания треугольника. Если мы знаем длины средней линии и основания треугольника, мы можем использовать теорему Пифагора для нахождения высоты треугольника. Формула для высоты треугольника: высота треугольника = √(длина средней линии^2 - (половина основания треугольника)^2). Это может быть полезно для вычисления высоты треугольника, когда у нас есть информация о длине средней линии и основания.
Средняя линия прямоугольного треугольника имеет много применений в решении задач. Она может помочь нам определить площадь, радиус вписанной окружности и высоту треугольника. Зная эти свойства, мы можем использовать среднюю линию в практических задачах различной сложности.
Примеры использования средней линии в реальной жизни
Средняя линия в прямоугольных треугольниках имеет широкий спектр применений в реальной жизни. Ниже приведены некоторые примеры:
- Строительство зданий: средняя линия может использоваться для вычисления расположения опорных столбов, балок и других конструкций.
- Дизайн интерьера: нахождение средней линии помогает создать гармоничное размещение мебели и других объектов в помещении.
- Медицина: при определении положения и кривизны позвоночника, средняя линия может быть использована в диагностике и лечении спинальных проблем.
- Графический дизайн: средняя линия может играть важную роль при создании симметричных и сбалансированных композиций.
- Спорт: в некоторых видов спорта, таких как гимнастика и фигурное катание, средняя линия используется для оценки положения и движения тела.
- Навигация: средняя линия может помочь в навигации при путешествиях на море или в горах.
- Архитектура и дизайн ландшафта: средняя линия может использоваться для планирования геометрических форм и создания симметрии в строительстве зданий и ландшафтным дизайне.
- Фотография: средняя линия может использоваться для создания баланса и направления в кадре.
Это только некоторые примеры использования средней линии в реальной жизни. Её геометрические свойства делают её полезной для многих областей деятельности.



