Треугольник – одна из самых изучаемых фигур в геометрии. Он имеет свои особенности и свойства, которые позволяют нам рассчитывать его параметры и характеристики. Одним из самых интересных и полезных параметров треугольника является его высота.
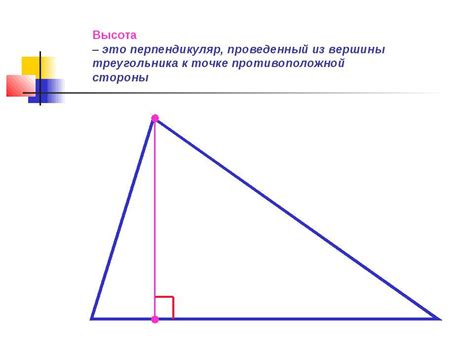
Высота треугольника – это отрезок, проведенный из вершины до основания и перпендикулярный к основанию. Зная длины сторон треугольника, можно вычислить его высоту с помощью специальной формулы. Формула высоты треугольника через стороны позволяет нам определить длину высоты без необходимости знать углы и другие параметры треугольника.
Формула высоты треугольника через стороны основана на принципе подобия треугольников. Два треугольника, имеющих параллельные стороны, признаются подобными. Однако, чтобы использовать эту формулу, треугольник должен быть остроугольным или прямоугольным. В случае тупоугольного треугольника, существует только одна высота – до наибольшего из трех его сторон.
Значение высоты треугольника и его применение в геометрии
Значение высоты треугольника имеет важное значение в геометрии. С помощью высоты треугольника можно решать различные задачи и находить значения других параметров треугольника. В основном, высота применяется для нахождения площади треугольника и доказательства различных теорем.
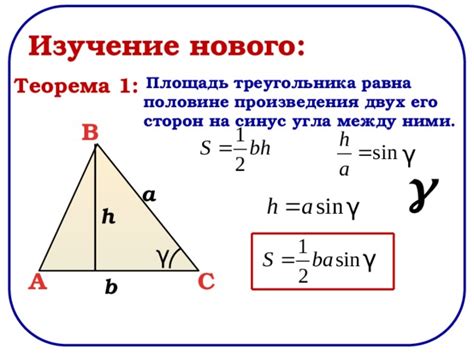
Для нахождения площади треугольника, можно использовать формулу высоты, которая гласит: площадь треугольника равна половине произведения основания треугольника и соответствующей ему высоты. Таким образом, если известны значения сторон треугольника, высота может быть найдена с помощью специальных формул и применена для вычисления площади.
Высота треугольника также используется в доказательстве различных доказательств и теорем. Например, принимая во внимание геометрические свойства высоты, можно доказать теоремы, такие как теорема о пирамиде, теорема о средних линиях треугольника и многое другое.
Таким образом, значение высоты треугольника в геометрии не может быть недооценено. Оно играет важную роль в вычислениях, доказательствах и конструкциях треугольников.
Изучение формулы высоты треугольника через стороны
Формула высоты треугольника через стороны позволяет нам найти высоту треугольника, зная длины его сторон. Эта формула основана на теореме Пифагора и может быть полезной в различных геометрических задачах и вычислениях.
Для применения формулы высоты треугольника через стороны нам необходимо знать длины всех трех сторон треугольника. Пусть a, b и c - длины сторон треугольника.
Формула высоты треугольника через стороны имеет вид:
h = 2 * (S / a)
где h - высота треугольника, S - площадь треугольника и a - длина одной из сторон треугольника.
Зная длины всех сторон треугольника и формулу высоты, мы можем легко вычислить значение высоты треугольника.
Например, пусть треугольник имеет стороны длиной 5, 12 и 13 единиц. Используем формулу высоты треугольника через стороны:
h = 2 * (S / a)
h = 2 * (30 / 5)
h = 2 * 6
h = 12
Таким образом, высота треугольника с сторонами 5, 12 и 13 равна 12 единицам.
Изучение формулы высоты треугольника через стороны позволяет нам легко решать задачи, связанные с треугольниками и их свойствами. Надеюсь, что этот обзор и примеры помогут вам лучше понять и применять данную формулу.
Обзор основных теорем и правил для применения формулы

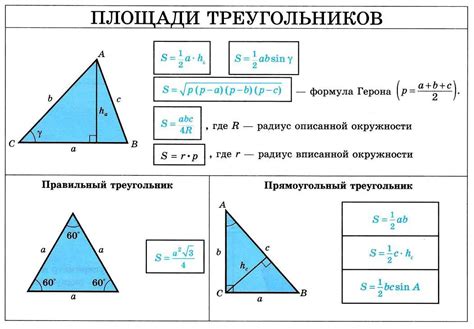
Для расчета высоты треугольника по формуле через стороны, необходимо учитывать несколько важных теорем и правил:
| Теорема о высоте треугольника | Теорема о высоте треугольника устанавливает, что высота треугольника, проведенная из вершины к основанию, является перпендикуляром к основанию. |
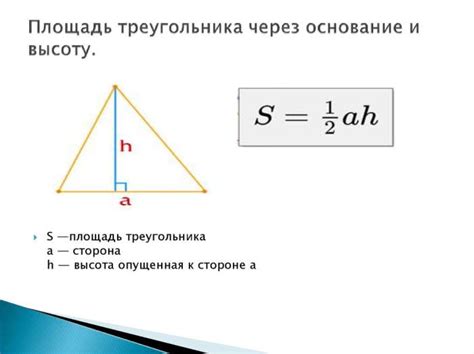
| Площадь треугольника | Площадь треугольника можно вычислить по формуле: S = 0.5 * a * h, где S - площадь треугольника, a - длина основания, h - высота треугольника. |
| Формула высоты треугольника через стороны | Формулу высоты треугольника через стороны можно записать как: h = 2 * S / c, где h - высота треугольника, S - площадь треугольника, c - длина стороны противолежащей высоте. |
| Значение высоты треугольника | Значение высоты треугольника зависит от длины основания и длины стороны противолежащей высоте. Как правило, высота треугольника меньше длины стороны противолежащей высоте. |
Правильное применение формулы позволяет точно определить высоту треугольника и использовать эту информацию в различных математических и геометрических расчетах.
Примеры решения задач с использованием формулы высоты треугольника
Ниже приведены несколько примеров решения задач, в которых используется формула высоты треугольника.
Задача: Найдите высоту треугольника ABC, если известны стороны AB = 8 см, BC = 6 см и AC = 10 см.
Решение: Применим формулу высоты треугольника:
- Полупериметр треугольника p = (AB + BC + AC) / 2 = (8 + 6 + 10) / 2 = 24 / 2 = 12 см
- Площадь треугольника S = √(p * (p - AB) * (p - BC) * (p - AC)) = √(12 * (12 - 8) * (12 - 6) * (12 - 10)) = √(12 * 4 * 6 * 2) = √(576) = 24 см²
- Высота треугольника h = 2 * S / AB = 2 * 24 / 8 = 6 см
Ответ: Высота треугольника ABC равна 6 см.
Задача: Найдите высоту прямоугольного треугольника DEF, если известны стороны DE = 10 см и DF = 8 см.
Решение: Для прямоугольного треугольника высота равна половине произведения катетов, поэтому:
- Высота треугольника h = (DE * DF) / 2 = (10 * 8) / 2 = 80 / 2 = 40 см
Ответ: Высота прямоугольного треугольника DEF равна 40 см.
Задача: В треугольнике XYZ сторона XY равна 12 см, а высота, опущенная на эту сторону, равна 8 см. Найдите площадь треугольника XYZ.
Решение: Используем формулу для площади треугольника через сторону и высоту:
- Площадь треугольника S = (XY * h) / 2 = (12 * 8) / 2 = 96 / 2 = 48 см²
Ответ: Площадь треугольника XYZ равна 48 см².
Разнообразные способы доказательства формулы

Один из способов доказательства формулы заключается в использовании подобия треугольников. Предположим, что у нас есть треугольник ABC, а его высота проведена из вершины A к основанию BC. Обозначим высоту через h, а стороны треугольника через a, b, и c. Заметим, что треугольники ABC и AHC являются подобными по двум углам, так как угол AHC равен прямому углу, а угол CAB равен основному углу. Используя соответствующие стороны подобных треугольников, можем составить пропорцию:
AC / BC = AH / AB
Заметим, что сторона AC равна h (высоте треугольника), сторона BC равна a (основанию треугольника), а сторона AB равна c (другой стороне треугольника). Таким образом, получаем пропорцию:
h / a = AH / c
Умножая обе части пропорции на a и деля на c, получаем окончательную формулу:
h = (a * AH) / c
Другой способ доказательства формулы заключается в использовании площадей треугольников. Пусть треугольник ABC имеет стороны a, b, и c, а его высота проведена из вершины A к основанию BC и равна h. Известно, что площадь треугольника ABC равна:
S_ABC = (1/2) * a * h
Заметим, что площадь треугольника ABC также может быть выражена через стороны треугольника по формуле Герона:
S_ABC = sqrt(s * (s - a) * (s - b) * (s - c))
где s - полупериметр треугольника, равный (a + b + c) / 2. Запишем это равенство:
(1/2) * a * h = sqrt(s * (s - a) * (s - b) * (s - c))
Возводя данное равенство в квадрат и упрощая выражения, получаем формулу для высоты треугольника через стороны:
h = (2 * sqrt(s * (s - a) * (s - b) * (s - c))) / a
Как видно из доказательств, формула высоты треугольника через стороны основывается на принципах подобия и площадей треугольников. Эта формула позволяет находить высоту треугольника, используя только его стороны, что является очень удобным для решения различных задач и заданий.
Доказательство формулы высоты треугольника через стороны
Формула для вычисления высоты треугольника может быть выражена через стороны треугольника и называется формулой Герона. Для доказательства этой формулы можно использовать принцип подобия треугольников.
Представим треугольник ABC, где стороны обозначаются как AB, BC и AC. Пусть h - высота, проведенная из вершины A.
Используя прямой угол, треугольникы ABC и AHB подобны. Коэффициент подобия между этими треугольниками равен отношению длин отрезков BH и BC. Таким образом, мы можем записать:
AB/AC = BH/BC
С помощью формулы подобия треугольников, мы можем переписать это выражение:
h/AC = BH/BC
Обратите внимание, что h - это длина высоты, а AC, BH и BC - это длины сторон треугольника.
Теперь мы можем переписать это выражение для высоты:
h = (BH/BC) * AC
Это и есть формула высоты треугольника через стороны. Она позволяет нам вычислить высоту треугольника, зная длины его сторон.
Доказательство этой формулы основано на принципе подобия треугольников и может быть использовано для вычисления высоты треугольника в различных задачах и приложениях.



