Геометрическая прогрессия - это последовательность чисел, в которой каждый следующий элемент получается умножением предыдущего на постоянное число q. Это важное понятие в математике, которое нашло применение во многих областях науки и практических задачах, таких как финансы, физика, информатика и т.д.
Каждая геометрическая прогрессия может быть описана формулой:
an = a1 * q^(n-1),
где a1 - первый член прогрессии, n - номер элемента, an - n-й член прогрессии, q - постоянное число, называемое знаменателем прогрессии.
Формула суммы геометрической прогрессии позволяет найти сумму всех элементов прогрессии, используя знаменатель q и количество элементов n:
Что такое геометрическая прогрессия?
Геометрическая прогрессия имеет следующий вид:
- a
- a * q
- a * q^2
- a * q^3
- ...
Здесь a – первый член прогрессии, а q – знаменатель. Знаменатель может быть как положительным, так и отрицательным числом. Если |q| > 1, то прогрессия называется возрастающей, если 0
Формула суммы геометрической прогрессии позволяет вычислить сумму первых n членов прогрессии и имеет вид:
S_n = a * (1 - q^n) / (1 - q),
где S_n – сумма первых n членов прогрессии.
Геометрические прогрессии широко применяются в математике, физике, экономике и других науках.
Значение геометрической прогрессии в математике
Одно из основных значений геометрической прогрессии заключается в ее использовании для нахождения суммы бесконечного ряда элементов. Формула суммы геометрической прогрессии позволяет эффективно вычислить сумму всех элементов прогрессии, даже если их количество бесконечно.
Геометрическая прогрессия также широко применяется в финансовых расчетах, экономике и статистике. Например, она может использоваться для моделирования роста населения, прогнозирования доходов или расчета аннуитетных платежей.
В геометрии геометрическая прогрессия используется для построения специальных кривых, таких как спираль Архимеда и экспоненциальные кривые. Эти кривые имеют множество приложений в различных областях, таких как физика, биология и инженерия.
Значение геометрической прогрессии в математике также проявляется в ее связи с другими математическими объектами и концепциями. Например, геометрическая прогрессия связана с экспоненциальной функцией и логарифмами, а также с бесконечными рядами и конечными суммами.
Таким образом, геометрическая прогрессия играет важную роль в математике и обладает широким спектром применений, от расчетов до моделирования и построения кривых.
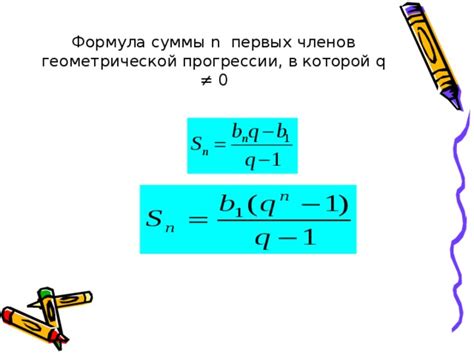
Формула для нахождения суммы геометрической прогрессии
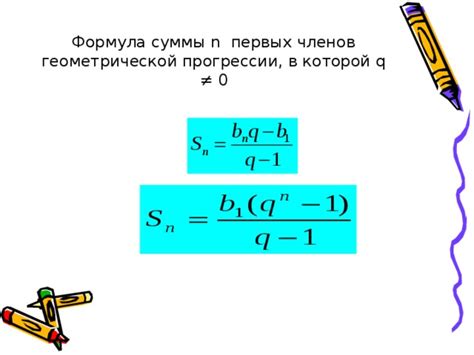
Формула суммы геометрической прогрессии позволяет вычислить сумму всех членов данной прогрессии на основе первого члена (а1), знаменателя (q) и количества членов (n).
Формула имеет следующий вид:
S = a1(1 - qn) / (1 - q)
где:
- S - сумма геометрической прогрессии;
- a1 - первый член прогрессии;
- q - знаменатель прогрессии;
- n - количество членов прогрессии.
Формула очень полезна при решении задач, связанных с прогрессиями, например, при расчете суммы процентов, ежемесячного платежа по кредиту или накопительного плана.
Использование данной формулы помогает упростить и ускорить процесс вычисления сумм геометрических прогрессий и предоставляет возможность получить точные результаты.
Общее понятие о факторе прогрессии (q)
Фактор прогрессии обозначается символом q. В геометрической прогрессии каждый следующий член получается умножением предыдущего на фактор прогрессии. Если первый член геометрической прогрессии равен a, то в общем виде члены прогрессии можно записать как: a, aq, aq^2, aq^3, ..., где q - фактор прогрессии.
Значение фактора прогрессии может быть как положительным, так и отрицательным. Если |q| 1 прогрессия называется расходящейся.
Фактор прогрессии играет важную роль при расчетах суммы геометрической прогрессии. Сумма геометрической прогрессии может быть вычислена по формуле: S_n = a * (1 - q^n) / (1 - q), где S_n - сумма первых n членов прогрессии, a - первый член прогрессии, q - фактор прогрессии.
Значение фактора прогрессии (q) в формуле суммы геометрической прогрессии
Значение фактора прогрессии (q) влияет на то, как увеличиваются или уменьшаются члены прогрессии. Если q больше единицы, то каждый следующий член прогрессии будет больше предыдущего. Если q меньше единицы, то каждый следующий член прогрессии будет меньше предыдущего. Если q равно единице, то члены прогрессии останутся постоянными.
Фактор прогрессии (q) можно выразить через любые два последовательных члена геометрической прогрессии с помощью следующей формулы:
q = (следующий член прогрессии) / (предыдущий член прогрессии)
Зная значение фактора прогрессии (q), можно использовать его в формуле суммы геометрической прогрессии для нахождения суммы всех членов прогрессии.
Значение фактора прогрессии (q) является важным параметром при работе с геометрическими прогрессиями, поскольку позволяет определить характер изменения и величину членов прогрессии.
Пример:
У нас есть геометрическая прогрессия со следующими значениями: 1, 2, 4, 8, 16. Здесь каждый следующий член прогрессии равен предыдущему члену, умноженному на 2. Значение фактора прогрессии (q) равно 2, так как каждый следующий член прогрессии равен 2 предыдущему члену.
Используя значение фактора прогрессии (q) и формулу суммы геометрической прогрессии, мы можем найти сумму всех членов этой прогрессии.
Примеры использования формулы для нахождения суммы геометрической прогрессии
Формула нахождения суммы геометрической прогрессии может быть полезной во многих ситуациях. Рассмотрим несколько примеров использования данной формулы:
Пример 1: Пусть у нас есть геометрическая прогрессия с первым членом a = 2 и множителем q = 3. Нам необходимо найти сумму первых 5 членов этой прогрессии.
Используя формулу суммы геометрической прогрессии:
S_n = a * (1 - q^n) / (1 - q),
где S_n - сумма первых n членов прогрессии, a - первый член прогрессии, q - множитель прогрессии, n - количество членов, получаем:
S_5 = 2 * (1 - 3^5) / (1 - 3) = 2 * (1 - 243) / (-2) = -482 / (-2) = 241.
Таким образом, сумма первых 5 членов данной геометрической прогрессии равна 241.
Пример 2: Пусть у нас есть геометрическая прогрессия с первым членом a = 1 и множителем q = 0.5. Нам необходимо найти сумму всех членов этой прогрессии.
Используя формулу суммы геометрической прогрессии:
S = a / (1 - q),
где S - сумма всех членов прогрессии, a - первый член прогрессии, q - множитель прогрессии, получаем:
S = 1 / (1 - 0.5) = 1 / 0.5 = 2.
Таким образом, сумма всех членов данной геометрической прогрессии равна 2.
Пример 3: Пусть у нас есть геометрическая прогрессия с первым членом a = 4 и множителем q = 2. Нам необходимо найти сумму первых 10 членов этой прогрессии.
Используя формулу суммы геометрической прогрессии:
S_n = a * (1 - q^n) / (1 - q),
где S_n - сумма первых n членов прогрессии, a - первый член прогрессии, q - множитель прогрессии, n - количество членов, получаем:
S_10 = 4 * (1 - 2^10) / (1 - 2) = 4 * (1 - 1024) / (-1) = -4096 / (-1) = 4096.
Таким образом, сумма первых 10 членов данной геометрической прогрессии равна 4096.
Это лишь некоторые примеры использования формулы для нахождения суммы геометрической прогрессии. В реальной жизни формула может применяться для решения задач в финансах, экономике, физике и других науках. Она позволяет нам быстро и точно вычислять сумму членов геометрической прогрессии, что является важным инструментом в различных областях знания.
