Dbce квадрат - это фигура, образованная конечным количеством точек C, d, b и e, которые образуют треугольник Cde. В данной статье мы рассмотрим формулу для нахождения площади квадрата Dbce, способы её расчёта и значения углов треугольника Cde.
Формула для нахождения площади квадрата Dbce имеет следующий вид:
S = d * e
Для расчёта площади квадрата необходимо знать значение длины сторон d и e. При этом, если сторона d равна стороне e, то квадрат Dbce называется равносторонним.
Значения углов треугольника Cde зависят от соотношений длин сторон d и e. В случае, если сторона d больше стороны e, то угол Cde будет острым. Если сторона d меньше стороны e, то угол Cde будет тупым. А если стороны d и e равны, то угол Cde будет прямым.
Итак, в данной статье мы рассмотрели формулу для нахождения площади квадрата Dbce, способы расчёта этой площади и значения углов треугольника Cde в зависимости от длин сторон. Используйте эти знания для решения задач и конструирования различных геометрических фигур.
Dbce квадрат: как рассчитать его значение?

Для расчета значения стороны Dbce необходимо знать длины сторон треугольника Cde и значения его углов.
Если известны значение угла Cde и длина стороны Cde, то можно использовать тригонометрические функции для нахождения значения стороны Dbce. Например, если известны длина стороны Cde и угол Cde, то длина стороны Dbce может быть найдена по формуле:
Dbce = Cde / sin(Cde)
Где sin(Cde) - синус угла Cde.
Если известны длины сторон Cde и Ecd, то можно использовать теорему Пифагора для нахождения длины стороны Dbce. Теорема Пифагора утверждает, что квадрат длины гипотенузы равен сумме квадратов длин катетов. Таким образом, для нахождения значения стороны Dbce можно использовать формулу:
Dbce = √(Cde² + Ecd²)
Где √ - квадратный корень.
Зная значения углов треугольника Cde, можно найти значения углов треугольника Dbce. Угол Dbc будет равен 90 градусов, угол Dbe можно найти как разность 180 градусов и суммы углов Dbc и Cbe:
Dbe = 180 - Dbc - Cbe
Таким образом, используя указанные формулы и значения углов и сторон треугольника Cde, можно рассчитать значение стороны Dbce и значения углов треугольника Dbce.
Формула и расчёт Dbce квадрата с помощью углов треугольника Cde
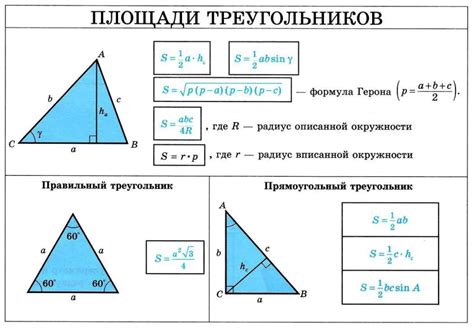
Угол Cde измеряется в градусах и обозначается символом α.
Определим, что Db = Bc = Ce = Ed = a, где a - сторона квадрата Dbce.
Также угол Cde равен 90 градусам (α = 90°).
Формула исходит из того, что в квадрате все стороны равны, а углы прямые:
P = 4a, где P - периметр квадрата, a - сторона квадрата.
S = a*a, где S - площадь квадрата, a - сторона квадрата.
Таким образом, для вычисления периметра и площади Dbce квадрата с помощью углов треугольника Cde достаточно знать длину одной из его сторон (a), а также угол Cde (α = 90°).
Значения углов треугольника Cde и их влияние на Dbce квадрат
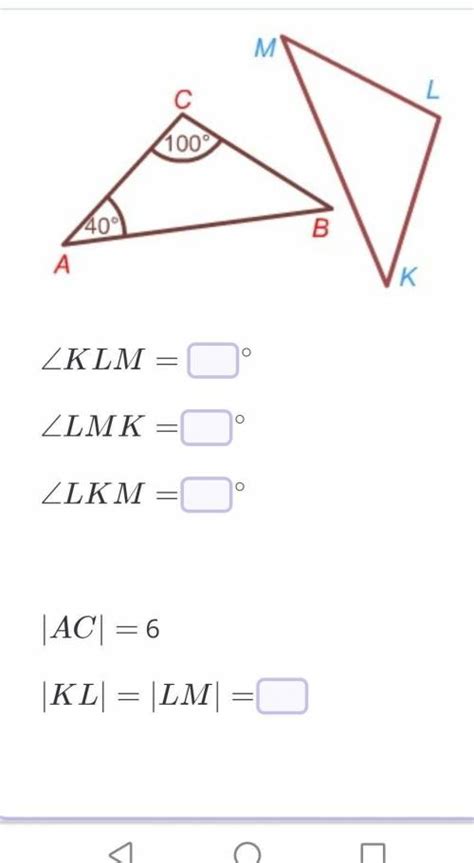
Углы треугольника Cde могут иметь различные значения, которые влияют на форму квадрата Dbce, образуемого этим треугольником.
Первый угол треугольника Cde:
α
Он определяет угол наклона верхней стороны квадрата Dbce. Если угол α маленький, то сторона квадрата Dbce будет практически параллельна оси C. Если угол α большой, то сторона Dbce будет сильно наклонена. Чем большее значение угла α, тем более наклоненной будет верхняя сторона квадрата Dbce.
Второй угол треугольника Cde:
β
Он определяет угол наклона правой стороны квадрата Dbce. Если угол β маленький, то правая сторона квадрата Dbce будет практически перпендикулярна оси D. Если угол β большой, то правая сторона Dbce будет значительно отклонена от перпендикулярности. Чем большее значение угла β, тем более наклоненной будет правая сторона квадрата Dbce.
Третий угол треугольника Cde:
γ
Он определяет угол наклона нижней стороны квадрата Dbce. Если угол γ маленький, то нижняя сторона квадрата Dbce будет практически параллельна оси C. Если угол γ большой, то нижняя сторона Dbce будет сильно наклонена. Чем большее значение угла γ, тем более наклоненной будет нижняя сторона квадрата Dbce.
Таким образом, значения углов треугольника Cde определяют наклон сторон квадрата Dbce относительно осей C и D. Эти углы влияют на форму и геометрию квадрата Dbce, делая его либо более параллельным оси C, либо более отклоненным от нормального положения.
Dbce квадрат: его свойства и особенности
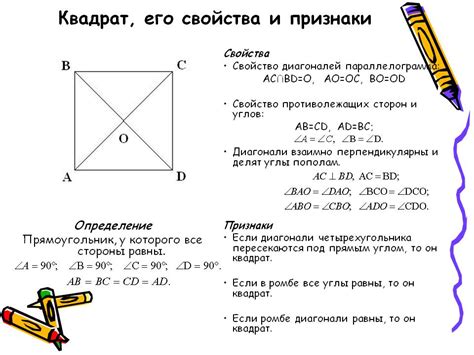
Основные свойства Dbce квадрата:
- Равные стороны: Все стороны Dbce квадрата имеют равную длину. Это свойство делает Dbce квадрат симметричным относительно своей оси.
- Равные углы: Все углы Dbce квадрата имеют равный размер. Каждый угол равен 90 градусам, что делает Dbce квадрат прямоугольным.
- Диагонали: Диагонали Dbce квадрата являются взаимоперпендикулярными и равными. Они делят квадрат на четыре равных треугольника.
- Площадь: Площадь Dbce квадрата можно вычислить, возведя в квадрат длину любой его стороны.
- Периметр: Периметр Dbce квадрата можно найти, умножив длину одной стороны на 4.
Dbce квадрат является основой для многих геометрических фигур и имеет множество применений в различных областях науки и техники. Он используется в строительстве, архитектуре и геодезии. Изучение свойств Dbce квадрата помогает понять основы геометрии и дает основу для изучения более сложных фигур.
Примеры расчетов Dbce квадрата с разными значениями углов треугольника Cde
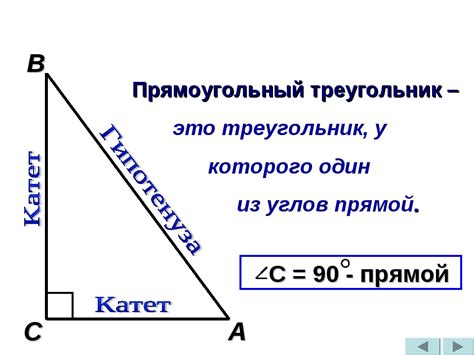
Для расчета Dbce квадрата с разными значениями углов треугольника Cde используется следующая формула:
Dbce = 2 * d * cos(E)
где:
- Dbce - длина стороны квадрата;
- d - длина стороны треугольника Cde;
- E - угол между сторонами треугольника Cde.
В таблице ниже представлены несколько примеров расчетов Dbce квадрата при различных значениях углов треугольника Cde:
| Значение угла E (в градусах) | Длина стороны треугольника Cde (d) | Длина стороны квадрата (Dbce) |
|---|---|---|
| 45 | 5 | 7.07 |
| 60 | 7 | 7 |
| 30 | 10 | 8.66 |
Из приведенных примеров видно, что при разных значениях углов треугольника Cde, длина стороны квадрата Dbce также изменяется. Это связано с тем, что Dbce зависит от угла E и длины стороны треугольника Cde.



