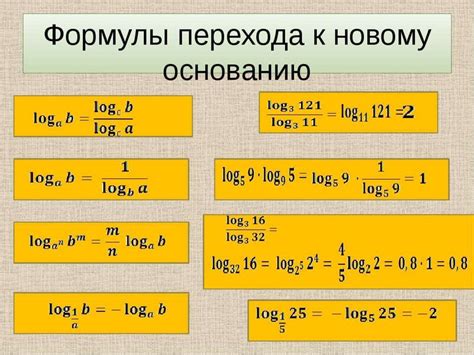
Логарифм – это одна из основных математических функций, которая позволяет нам найти ответ на вопрос: в какую степень нужно возвести число, чтобы получить заданное число. Одним из наиболее популярных логарифмов является логарифм по основанию 2.
Если говорить о логарифме 32 по основанию 2, то это означает, что мы ищем число, возводя которое в степень 2, получим 32. Математически это можно записать следующим образом: 2^x = 32, где x – искомый логарифм, равный логарифму 32 по основанию 2.
Чтобы найти значение логарифма 32 по основанию 2, нужно решить уравнение 2^x = 32. Для этого нам понадобится метод десятичных логарифмов. Применяя его, мы получаем следующий расчет: x = log₂32 = log₂(2^5) = 5.
Определение логарифма

Общая формула для вычисления логарифма:
| logb(x) = y | - где: |
| b - основание логарифма | |
| x - аргумент логарифма | |
| y - результат (показатель степени) |
В случае, когда основание логарифма b не указано, считается, что оно равно 10 (логарифм называется десятичным).
Основание логарифма

Основание логарифма определяет, в какой системе счета проводятся вычисления. Наиболее распространены логарифмы по основанию 10 (десятичные логарифмы) и логарифмы по основанию e (натуральные логарифмы), где e – математическая константа, приближенное значение которой равно 2,71828.
Логарифмы по основанию 2 также являются важными и широко применяются в математике и компьютерных науках. Они позволяют решать множество задач, связанных с двоичной системой счисления и информационными технологиями.
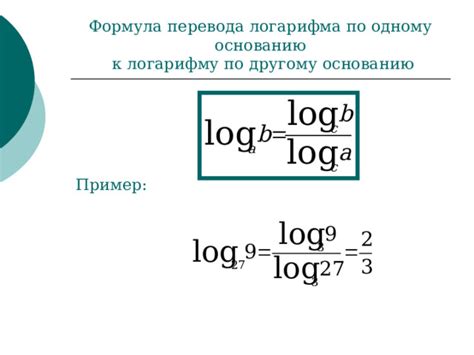
Для вычисления логарифма числа 32 по основанию 2 можно воспользоваться формулой:
log2(32) = x
Чтобы найти значение логарифма, нужно найти показатель степени, в которую нужно возвести основание (2), чтобы получить число (32). В данном случае результат будет равен 5, так как 25 = 32.
Таким образом, логарифм 32 по основанию 2 равен 5.
Формула логарифма по основанию 2
Логарифм по основанию 2 выражает степень, в которую нужно возвести число 2, чтобы получить данное число. Формула логарифма по основанию 2 выглядит следующим образом:
log2(x) = y
где:
- log2 - логарифм по основанию 2
- x - число, для которого ищем логарифм
- y - результат, степень, в которую нужно возвести 2, чтобы получить число x
Например, если мы хотим найти логарифм по основанию 2 числа 32, мы используем формулу:
log2(32) = y
Чтобы решить данное уравнение, мы ищем значение y, которое будет удовлетворять уравнению:
2y = 32
Раскрывая 2 в виде степени, получаем:
2y = 25
так как 25 = 32, значит, ответом на данное уравнение будет:
y = 5
Таким образом, логарифм числа 32 по основанию 2 равен 5.
Использование формулы для вычисления логарифма 32 по основанию 2

Формула для вычисления логарифма по основанию 2 имеет вид:
log2 32 = y
Чтобы найти значение логарифма 32 по основанию 2, необходимо найти степень, в которую нужно возвести основание (2), чтобы получить результат (32). В данном случае необходимо найти значение показателя степени (y).
Решение данной задачи можно провести путем последовательного возведения основания в степень, пока не будет достигнуто значение 32:
- 21 = 2
- 22 = 4
- 23 = 8
- 24 = 16
- 25 = 32
Таким образом, логарифм 32 по основанию 2 равен 5, так как основание 2 нужно возвести в степень 5, чтобы получить значение 32.
Используя формулу и проводя вычисления, можно определить значение логарифма любого числа по заданному основанию.
Пример расчетов логарифма 32 по основанию 2
Чтобы найти логарифм числа 32 по основанию 2, нам необходимо выяснить, в какую степень нужно возвести число 2, чтобы получить 32. То есть, мы ищем значение x в уравнении 2^x = 32.
Для решения этого уравнения, мы можем записать число 32 как степень 2: 2^5 = 32. Значит, логарифм 32 по основанию 2 равен 5.
Таким образом, логарифм числа 32 по основанию 2 равен 5.



