Евклидова геометрия, названная в честь древнегреческого математика Евклида, является основой классической геометрии. В евклидовой геометрии основное понятие – прямая линия, на которой любые две точки могут быть соединены самым коротким путем, то есть отрезком прямой линии. Другими словами, в евклидовой геометрии выполняется пятый постулат Евклида, который гласит, что через любую точку, не лежащую на данной прямой, можно провести только одну прямую, параллельную данной.
Однако, неевклидова геометрия различается с евклидовой по своим основополагающим принципам. Неевклидова геометрия представляет собой геометрию, в которой не выполняется пятый постулат Евклида. Изменение этого постулата приводит к появлению новых и отличных от евклидовой свойств геометрии. В неевклидовой геометрии существуют геометрии с неограниченным или ограниченным числом параллельных прямых, а также геометрии с отрицательной или положительной кривизной.
Неевклидова геометрия имеет широкий спектр применений в физике и космологии. Она позволяет рассматривать пространство и время с точки зрения общей теории относительности, где пространство может быть кривым и зависеть от распределения масс, а время может течь с различной скоростью в разных областях.
Основы евклидовой геометрии
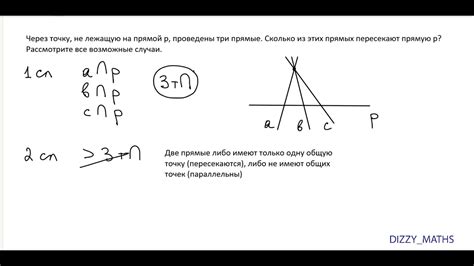
Основными принципами евклидовой геометрии являются:
- Аксиома о пространстве: существует бесконечное трехмерное евклидово пространство.
- Аксиома о точке: точка - это объект без размеров, обозначаемый заглавной буквой латинского алфавита.
- Аксиома об отрезке: отрезок - это часть прямой между двумя точками. Он имеет длину и может быть измерен с помощью единицы измерения.
- Аксиома об угле: угол - это область пространства между двумя лучами с общим началом, измеряемая в градусах или радианах.
- Аксиома о прямой: прямая - это бесконечно продолжающаяся и однородная фигура, состоящая из бесконечного числа точек.
Определение и принципы

Евклидова геометрия основана на системе аксиом, сформулированных греческим математиком Евклидом в III веке до н.э. Основной принцип евклидовой геометрии заключается в том, что через любые две точки можно провести прямую, а на прямой можно взять только одну точку, не принадлежащую этой прямой.
Неевклидова геометрия отличается от евклидовой тем, что она строится на других аксиомах. Основные принципы неевклидовой геометрии сформулированы двумя математиками - Бертраном и Лобачевским в начале XIX века. Главное отличие неевклидовой геометрии от евклидовой заключается в изменении аксиом, касающихся параллельных прямых. В неевклидовой геометрии существуют различные способы определения параллельных линий, и при этом выполняться могут различные аксиомы, не противоречащие логике и координационной геометрии.
Таким образом, отличие между евклидовой и неевклидовой геометрией заключается в аксиомах, на которых они основаны, и в свойствах параллельных прямых.
| Евклидова геометрия | Неевклидовая геометрия |
|---|---|
| Основана на аксиомах Евклида | Основана на других аксиомах |
| Утверждает, что через любые две точки можно провести прямую | Существуют различные способы определения параллельных линий |
| На прямой можно взять только одну точку, не принадлежащую этой прямой |
Элементы и свойства
Евклидова геометрия и неевклидова геометрия предлагают различные способы изучения и описания пространства. Вот некоторые из основных элементов и свойств, которые отличают эти два вида геометрии:
| Элемент/Свойство | Евклидова геометрия | Неевклидовая геометрия |
|---|---|---|
| Аксиомы | Евклидовы аксиомы - набор правил, на которых основана классическая геометрия Евклида. | Неевклидовы аксиомы - набор правил, нарушающих одну или несколько из евклидовых аксиом. |
| Постулаты | В евклидовой геометрии существуют три основных постулата, которые определяют понятия прямой, плоскости, и расстояния. | В неевклидовой геометрии постулаты могут быть модифицированы или заменены, чтобы создать топологические и геометрические пространства с другими свойствами. |
| Расстояние | В евклидовой геометрии расстояние между двумя точками считается прямой линией и вычисляется с использованием теоремы Пифагора. | В неевклидовой геометрии расстояние может определяться по-разному. Например, в гиперболической геометрии расстояние между точками изменяется соответственно кривизне пространства. |
| Сумма углов | В евклидовой геометрии сумма углов треугольника всегда равна 180 градусам. | В неевклидовой геометрии сумма углов может быть больше или меньше 180 градусов в зависимости от геометрических свойств пространства. |
Элементы и свойства евклидовой и неевклидовой геометрии позволяют представлять и анализировать различные виды пространств и форм. Неевклидова геометрия стала основой для развития новых математических и физических теорий, а евклидова геометрия остается применимой в большинстве практических задач и конструкций.
Евклидова геометрия в пространстве

Пространство в евклидовой геометрии представляет собой множество всех возможных точек, имеющих три координаты: x, y и z. Основные принципы евклидовой геометрии включают аксиомы о существовании прямой, соединяющей две точки, и о существовании прямой, параллельной данной прямой и проходящей через данную точку. Также важным принципом является аксиома о равенстве углов и длин отрезков.
В евклидовой геометрии можно изучать различные фигуры, такие как прямые, плоскости, окружности, их взаимное расположение и свойства. Для измерения длины отрезков и углов в евклидовой геометрии используется евклидово расстояние и меру угла.
Евклидова геометрия является основой для многих других областей математики и находит применение в физике, инженерии и других науках. Однако в реальном мире все объекты и пространства не всегда соответствуют модели евклидовой геометрии. Это привело к разработке неевклидовых геометрий, которые изучают пространства с нестандартной геометрией.
Равенство и параллельность
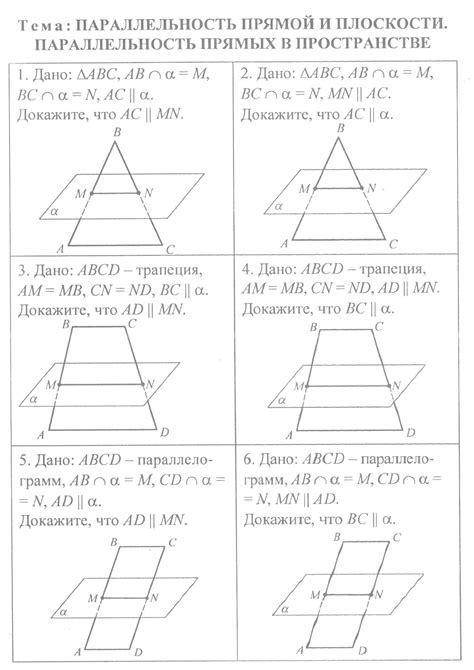
В неевклидовой геометрии, такой как гиперболическая геометрия и эллиптическая геометрия, отсутствует свойство равенства прямых. В гиперболической геометрии нет параллельных прямых, и любые две прямые обязательно пересекаются. В эллиптической геометрии, наоборот, все прямые являются параллельными и не пересекаются.
Понятие параллельности в неевклидовой геометрии имеет существенные отличия от евклидовой геометрии. В гиперболической геометрии параллельные прямые располагаются на постоянном расстоянии друг от друга, увеличиваясь при удалении. В эллиптической геометрии параллельные прямые сходятся и пересекаются в бесконечности, а расстояние между ними уменьшается с удалением.
Связь между прямыми и плоскостями
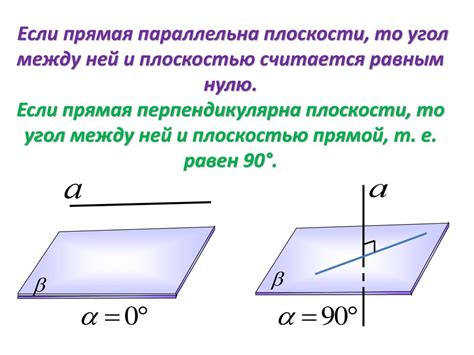
Евклидова геометрия:
В евклидовой геометрии связь между прямыми и плоскостями основана на аксиоме Евклида, известной как аксиома параллельных прямых. Согласно этой аксиоме, через любую точку, не принадлежащую данной прямой, проходит единственная параллельная ей прямая. Таким образом, прямые, лежащие в одной плоскости, никогда не пересекаются и называются параллельными.
Пример: На клетчатой бумаге можно провести две параллельные прямые, которые никогда не пересекутся, даже при продолжении насквозь.
Неевклидовая геометрия:
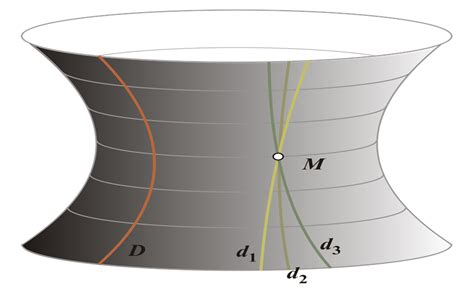
В неевклидовой геометрии связь между прямыми и плоскостями отличается от евклидовой геометрии. Например, в геометрии Лобачевского введена аксиома о параллельных прямых, которая гласит, что через любую точку, не лежащую на данной прямой, можно провести неограниченное количество прямых, которые не пересекают данную прямую. В такой геометрии прямые, лежащие в одной плоскости, не являются параллельными и могут пересекаться.
Пример: На сфере можно провести две прямые, которые на первый взгляд пересекаются, однако при продолжении на поверхности сферы образуют замкнутую кривую, не пересекающую себя.
Неевклидова геометрия
Главное отличие неевклидовых геометрий заключается в том, что они предполагают существование пространств с неевклидовой геометрией, которые не следуют аксиомам Евклида. Такие пространства исследуются в рамках различных неевклидовых геометрий, таких как сферическая геометрия и гиперболическая геометрия.
Сферическая геометрия рассматривает пространство на поверхности сферы. Одной из основных отличительных черт сферической геометрии является то, что сумма углов треугольника в сферической геометрии всегда превышает 180 градусов.
Гиперболическая геометрия, напротив, рассматривает пространство с постоянной отрицательной кривизной. В гиперболической геометрии сумма углов треугольника всегда меньше 180 градусов.
Неевклидова геометрия имеет важное значение в современной физике, особенно в области общей теории относительности. Применение неевклидовой геометрии позволяет описывать кривизну пространства и времени в уравнениях Эйнштейна.
Особенности и отличия

Основное отличие между евклидовой и неевклидовой геометрией заключается в параллельных линиях. В евклидовой геометрии существует аксиома, которая утверждает, что через точку, не принадлежащую прямой, проходит только одна прямая, параллельная данной. В неевклидовой геометрии же, наоборот, существуют параллельные прямые, проходящие через данную точку. Это противоречит постулату евклидовой геометрии и является основным отличием этих двух ветвей.
Также неевклидова геометрия имеет другие особенности, такие как кривизна пространства и отличающиеся свойства треугольников. В то время как в евклидовой геометрии сумма углов треугольника равна 180 градусам, в неевклидовой геометрии она может быть больше или меньше этого значения.



