Взаимное расположение плоскостей – одна из основных задач в геометрии, которая требует внимания и точных расчетов. Плоскости могут пересекаться, быть параллельными или скрещиваться под углом. Определить пересечение плоскостей можно с помощью различных методов, которые используются в математике и инженерии.
Одним из основных методов определения пересечения плоскостей является аналитический метод. Он основан на использовании координатной системы и алгебраических уравнений плоскостей. Для определения пересечения двух плоскостей необходимо составить и решить систему уравнений, состоящую из уравнений плоскостей. Если система имеет решение, то плоскости пересекаются в точке или прямой, в зависимости от их взаимного положения.
Для упрощения расчетов и определения пересечения плоскостей можно также использовать графический метод. С его помощью плоскости представляются в виде графиков на плоскости, что позволяет визуально определить их взаимное положение. При этом пересечение плоскостей будет обозначаться точкой или линией, их параллельность – параллельными линиями, а скрещивание под углом – наклонными линиями.
Взаимное расположение двух плоскостей
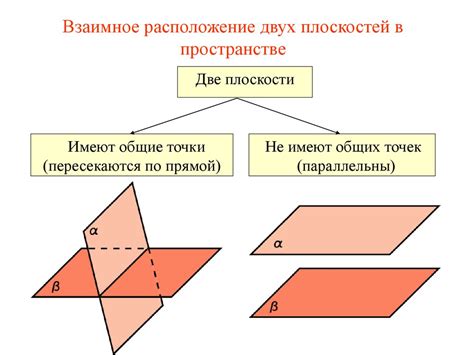
Взаимное расположение двух плоскостей может быть определено с помощью различных методов и алгоритмов. Рассмотрим некоторые из них:
- Способ 1: Метод плоскостных координат. Для определения взаимного расположения двух плоскостей можно ввести плоскостные координаты и записать уравнения этих плоскостей в виде общего уравнения плоскости. Затем можно рассмотреть систему этих уравнений и применить методы решения системы линейных уравнений для определения пересечения или параллельности плоскостей.
- Способ 2: По углу между нормалями. Если известны нормали к плоскостям, то взаимное расположение можно определить по углу между нормалями. Если угол между нормалями равен 90 градусам, то плоскости пересекаются. Если угол равен 0 градусам, то плоскости параллельны. В остальных случаях плоскости могут быть скользящими или пересекающимися в прямом направлении.
- Способ 3: Использование точек. Для определения пересечения плоскостей можно использовать точки. Если существует хотя бы одна общая точка на обеих плоскостях, то они пересекаются. Если общая точка отсутствует, то плоскости могут быть параллельны.
Различные методы и алгоритмы позволяют определить взаимное расположение двух плоскостей и выявить их пересечение или параллельность. Они находят применение в различных областях, включая геометрию, компьютерную графику и космическую навигацию.
Как определить пересечение?
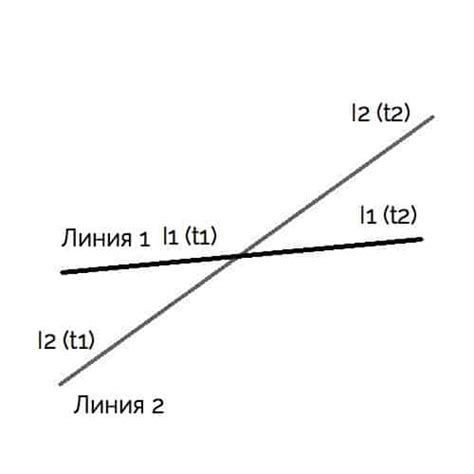
Для определения пересечения двух плоскостей необходимо найти общую точку или линию, которая одновременно принадлежит обеим плоскостям. Существует несколько способов решения этой задачи.
1. Метод аналитической геометрии.
Можно использовать уравнения плоскостей и систему уравнений для определения точки пересечения. Зная уравнения обеих плоскостей, можно составить систему уравнений и найти значения переменных, соответствующие точке пересечения плоскостей.
2. Метод векторов.
Для определения пересечения можно использовать векторное произведение нормалей плоскостей. Если векторное произведение равно нулевому вектору, значит плоскости совпадают или параллельны друг другу. Если векторное произведение не равно нулевому вектору, то оно определяет нормаль точки пересечения, а координаты этой точки можно найти из системы уравнений, составленной из уравнений плоскостей.
3. Графический метод.
Можно построить две плоскости на графике и найти точку пересечения, используя пересечение прямых, полученных проекцией плоскостей на плоскость проекций.
В любом случае, для определения пересечения плоскостей потребуется анализ уравнений или графиков, и в некоторых случаях может потребоваться использование дополнительных методов.
Методы определения пересечения двух плоскостей
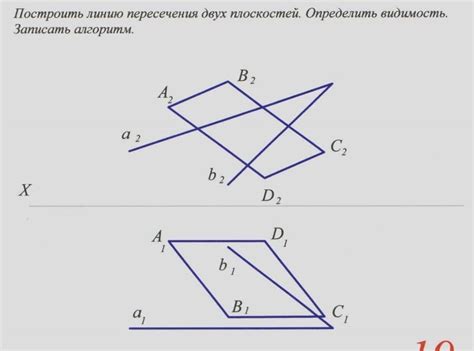
Пересечение двух плоскостей может быть определено различными методами. Некоторые из них включают:
- Метод аналитической геометрии: данный метод основан на использовании уравнений плоскостей. Путем решения системы линейных уравнений, определяются координаты пересечения плоскостей.
- Метод векторов: с помощью векторных операций можно вычислить точку пересечения плоскостей. Для этого необходимо найти пересечение нормалей к плоскостям.
- Метод геометрической интерпретации: данный метод основан на графическом представлении плоскостей. Путем построения пересекающихся прямых или плоскостей, определяется точка пересечения.
Выбор метода зависит от специфики задачи и доступных инструментов. Некоторые методы могут быть более эффективными или удобными в конкретных случаях. Важно учитывать особенности каждого метода и выбрать наиболее подходящий для данной ситуации.
Проверка условий пересечения плоскостей
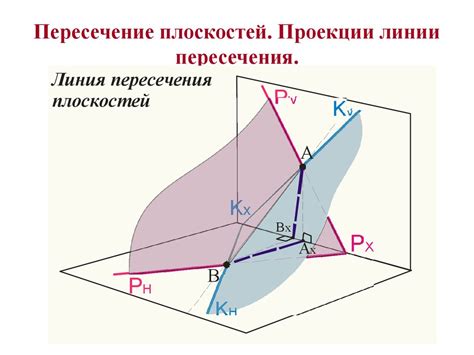
Пересечение двух плоскостей возможно, если выполняются определенные условия.
Одно из основных условий - плоскости должны быть не параллельны друг другу. Если уравнения плоскостей имеют одинаковые коэффициенты при переменных, то они параллельны и не пересекаются. Для определения этого условия можно выполнить сравнение коэффициентов при переменных в уравнениях плоскостей.
Второе условие - плоскости не должны совпадать. Если уравнения плоскостей одинаковы, то плоскости совпадают и также не пересекаются. Для проверки этого условия можно выполнить сравнение уравнений плоскостей.
Если оба условия не выполняются, то плоскости пересекаются и точка пересечения может быть найдена путем решения системы уравнений, состоящей из уравнений плоскостей.
Для наглядного представления условий пересечения плоскостей, можно воспользоваться таблицей:
| Условие | Плоскости пересекаются? |
|---|---|
| Плоскости не параллельны и не совпадают | Да |
| Плоскости параллельны | Нет |
| Плоскости совпадают | Нет |
Геометрическая интерпретация пересечения плоскостей
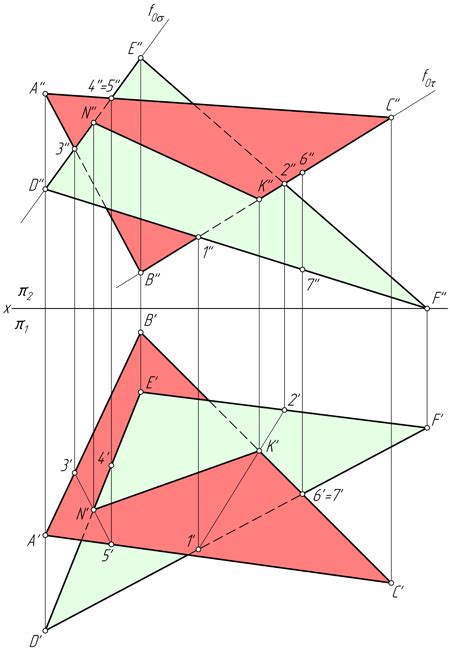
Две плоскости могут пересекаться или быть параллельными друг другу в трехмерном пространстве. Геометрическая интерпретация пересечения плоскостей заключается в определении, каким образом они взаимодействуют и какие точки принадлежат обеим плоскостям.
Если две плоскости пересекаются, то они имеют одну общую прямую-пересечение. Точки этой прямой лежат одновременно на обеих плоскостях. Форма и расположение прямой-пересечения зависит от угла между плоскостями и их направляющих векторов.
В случае, когда две плоскости параллельны друг другу, они никогда не пересекаются. В этом случае, плоскости можно представить как две параллельные бесконечные плоскости, которые не имеют общих точек.
Геометрическое представление пересечения плоскостей позволяет визуализировать и понять их взаимное расположение и связь друг с другом. Это важно для решения геометрических задач и применения математических методов в различных областях, таких как инженерия, архитектура, физика и компьютерная графика.
Расстояние между плоскостями
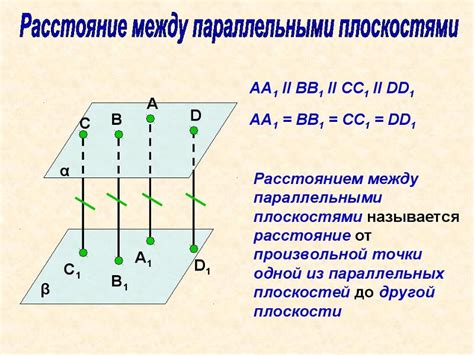
Расстояние между двумя параллельными плоскостями можно определить с помощью формулы, которая основана на их нормальных векторах и константах. Для этого нужно знать уравнения данных плоскостей в виде:
| Уравнение плоскости | ax + by + cz + d = 0 |
|---|
при условии, что векторы (a, b, c) и (a', b', c') являются нормальными векторами плоскостей.
Расстояние между плоскостями можно найти по следующей формуле:
d = |d'| / √(a^2 + b^2 + c^2)
где d' - это расстояние от начала координат до одной из плоскостей, а (a, b, c) - нормальный вектор этой плоскости.
Таким образом, зная уравнения плоскостей и их нормальные векторы, можно легко определить расстояние между плоскостями и использовать это знание, например, для построения графических моделей или решения геометрических задач.
Примеры реального пересечения плоскостей
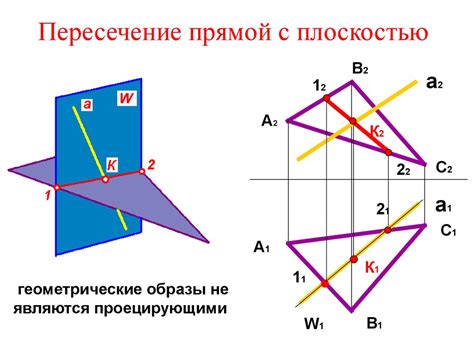
Взаимное расположение плоскостей и их пересечение широко встречается в различных областях науки и техники. Вот несколько примеров, иллюстрирующих реальные ситуации, где важно определить пересечение двух плоскостей:
| Пример | Область применения |
|---|---|
| Проектирование зданий | В архитектуре и строительстве взаимное расположение плоскостей играет важную роль при проектировании зданий. Например, при создании плана этажа, необходимо учесть пересечение различных плоскостей, таких как стены, полы и потолок, чтобы создать функциональное и эстетически приятное пространство. |
| Машиностроение | В инженерной отрасли пересечение плоскостей используется в процессе конструирования и создания деталей машин и механизмов. Например, при разработке кузова автомобиля необходимо учесть соприкосновение плоскостей, чтобы обеспечить правильные геометрические характеристики и функциональность конструкции. |
| Геодезия | В геодезии и картографии пересечение плоскостей применяется для определения координат и геометрических параметров при измерении и картографировании земной поверхности. Например, при создании топографических карт необходимо учесть пересечение плоскости земли с плоскостью горизонта, чтобы получить точные данные о рельефе местности и расположении объектов. |
Это лишь некоторые примеры применения взаимного расположения плоскостей и их пересечения. В каждой отрасли науки и техники существуют свои специфические задачи и методы определения пересечения плоскостей, которые помогают решать сложные проблемы и достигать качественных результатов.



