Пересечение двух прямых является одной из важных операций в геометрии. Данная операция позволяет определить точку, в которой данные прямые пересекаются. Знание о способах проверки пересечения прямых и понимание значения этого пересечения есть необходимость для решения множества математических и практических задач.
Одним из основных способов проверки пересечения двух прямых является аналитический метод. Он основан на решении системы уравнений, которая состоит из уравнений данных прямых. Для определения пересечения прямых используются последовательные шаги решения системы с использованием методов математического анализа, включая методы подстановки и методы сложения.
Значение пересечения прямых наиболее часто выражается координатами точки, в которой прямые пересекаются. Однако, это значение может иметь и другое толкование. Например, в контексте физики, пересечение двух прямых может означать точку, в которой два объекта сталкиваются. Поэтому изучение и понимание значения пересечения прямых позволяет применять эту операцию в различных областях науки и техники.
Значение пересечения двух прямых на плоскости
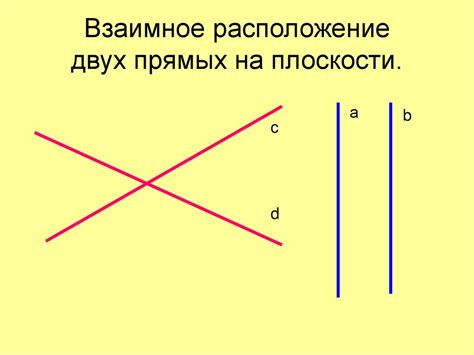
Если две прямые пересекаются, то их точка пересечения определяется математически. Для этого нужно решить систему уравнений, составленных по уравнению прямых. Решением этой системы будут координаты точки пересечения (x, y) на плоскости.
Значение пересечения двух прямых может иметь разные геометрические интерпретации:
- Если точка пересечения находится внутри отрезков, образованных прямыми, то это может означать, что объекты пересекаются внутри заданной области.
- Если точка пересечения находится на продолжении одного или обоих отрезков, то это может означать, что объекты пересекаются вне заданной области.
- Если точка пересечения находится вне отрезков и не лежит на их продолжении, то это может означать, что объекты не пересекаются вообще.
- Если прямые параллельны, то их точки пересечения нет. Значит, объекты не пересекаются и не имеют общих точек на плоскости.
Значение пересечения двух прямых на плоскости помогает анализировать их взаимное положение и геометрические свойства. Оно может быть использовано при решении различных задач в математике и геометрии, а также в приложениях, связанных с построением и измерением объектов на плоскости.
Как определить, пересекаются ли две прямые?
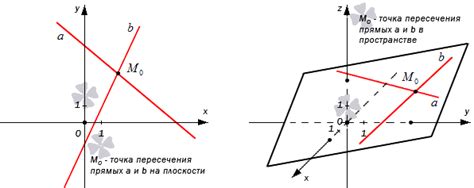
Для определения пересечения двух прямых можно использовать несколько способов:
1. Метод аналитической геометрии. Для этого необходимо записать уравнения прямых в общем виде и решить систему уравнений. Если система имеет единственное решение, то прямые пересекаются в этой точке. Если система не имеет решений или имеет бесконечное количество решений, то прямые не пересекаются.
2. Графический метод. Для этого нужно построить графики прямых на координатной плоскости и изучить их взаимное расположение. Если графики пересекаются в какой-то точке, то прямые пересекаются. Если графики не пересекаются и не параллельны, то прямые скрещиваются в бесконечности. Если графики параллельны, то прямые не пересекаются ни в какой точке.
3. Равенство параметрических уравнений. Если две прямые заданы параметрическими уравнениями и значения параметров удовлетворяют условию равенства, то прямые пересекаются. Если значения параметров не удовлетворяют условию равенства или хотя бы один из параметров равен бесконечности, то прямые не пересекаются.
Геометрический способ проверки пересечения прямых
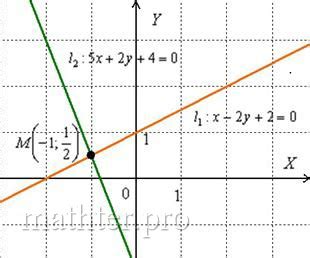
Для проверки пересечения двух прямых можно воспользоваться геометрическим методом.
В данном способе используется отрезок, называемый остатком, которым измеряют расстояние между прямыми. Если остаток равен нулю, то прямые совпадают, если остаток больше нуля, то прямые пересекаются, и если остаток меньше нуля, то прямые не пересекаются.
Для определения остатка необходимо выбрать произвольную точку на одной из прямых и провести через нее перпендикуляр к другой прямой. Далее измерить расстояние от точки пересечения перпендикуляра с другой прямой до начала перпендикуляра.
Если полученное расстояние положительное, то прямые пересекаются. Если расстояние равно нулю, то прямые совпадают. Если расстояние отрицательное, то прямые не пересекаются.
Геометрический способ проверки пересечения прямых имеет широкое применение в геометрии, особенно при решении задач, связанных с поиском точек пересечения прямых.
Метод аналитической геометрии для определения пересечения прямых
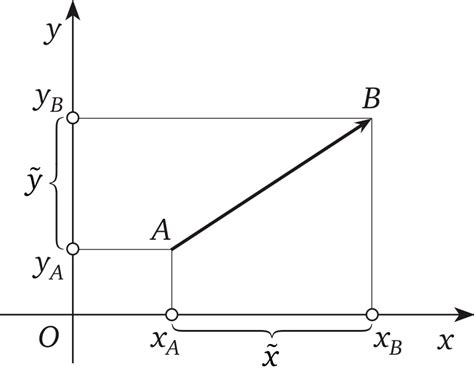
Одним из таких методов является метод с использованием уравнений прямых. Для начала, необходимо иметь уравнения двух прямых, которые пересекаются. Эти уравнения обычно представляются в виде уравнений прямых вида:
- y = k1*x + b1
- y = k2*x + b2
где k1 и k2 - коэффициенты наклона, а b1 и b2 - свободные члены уравнений.
Для того, чтобы найти точку пересечения двух прямых, необходимо решить систему уравнений, составленную из этих двух уравнений. Проще всего это сделать, используя метод подстановки или метод сложения/вычитания уравнений.
Сначала рассмотрим метод подстановки. Для этого выражаем y из одного уравнения и подставляем его в другое уравнение:
- y = k1*x + b1
- y = k2*x + b2
Затем приравниваем полученные выражения:
k1*x + b1 = k2*x + b2
Далее находим x, решая это уравнение:
x = (b2 - b1) / (k1 - k2)
И, наконец, подставляем найденное x в любое из исходных уравнений, чтобы найти y:
y = k1*x + b1
Таким образом, мы получаем точку пересечения прямых с координатами (x, y).
Другой метод, который можно использовать для нахождения точки пересечения прямых - это метод сложения/вычитания уравнений. Необходимо сложить или вычесть два уравнения между собой так, чтобы коэффициенты при одной из переменных сократились:
- k1*x + b1 = k2*x + b2
- k1*x - k2*x = b2 - b1
- (k1 - k2)*x = b2 - b1
После этого находим x, разделив обе части уравнения на (k1 - k2):
x = (b2 - b1) / (k1 - k2)
Аналогично методу подстановки, находим y, подставив найденное x в любое из исходных уравнений:
y = k1*x + b1
Применение данных методов аналитической геометрии позволяет определить точку пересечения двух прямых, что имеет большое значение в различных областях, таких как инженерия, физика, геометрия и астрономия.
Уравнения прямых и их взаимное расположение
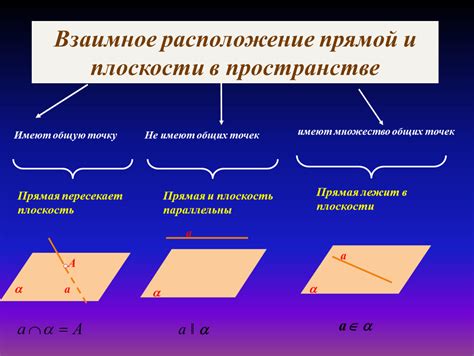
Для определения взаимного расположения двух прямых необходимо знать их уравнения. Уравнение прямой в общем виде имеет вид:
Аx + By + C = 0,
где A, B и C - это коэффициенты, определяющие угловой коэффициент и смещение прямой.
Если уравнения двух прямых заданы, можно использовать следующие приемы для определения их взаимного расположения:
- Если угловые коэффициенты (A1/A2) прямых равны, то прямые параллельны или совпадают;
- Если угловые коэффициенты (A1/A2) прямых имеют противоположные знаки, то прямые пересекаются;
- Если угловые коэффициенты прямых равны, а смещения (C1/C2) различны, то прямые скрещиваются;
- Если угловые коэффициенты прямых равны, а смещения (C1/C2) равны, то прямые совпадают;
- Если угловые коэффициенты (A1/A2) прямых бесконечны и смещения противоположны, то прямые параллельны и смещены;
- Если угловые коэффициенты (A1/A2) прямых бесконечны и смещения равны, то прямые совпадают.
Знание уравнений прямых и их взаимного расположения очень полезно при решении задач геометрии, особенно в аналитической геометрии. Это позволяет определить точки пересечения прямых, а также определить, параллельны ли они или совпадают.
Классификация пересечения прямых

- Лежать вне осей координат;
- Находиться на оси координат;
- Проходить через точку пересечения двух других прямых;
- Совпадать с одной из прямых;
- Совпадать с другой прямой и не иметь точки пересечения;
- Не иметь точки пересечения и находиться параллельно другой прямой;
- Не иметь точки пересечения и находиться перпендикулярно другой прямой;
Классификация пересечения прямых является важной при решении геометрических задач и проведении анализа геометрических фигур. Выявление типа пересечения позволяет определить дополнительные свойства прямых и использовать их в дальнейших вычислениях и конструкциях.
Взаимное расположение прямых в пространстве
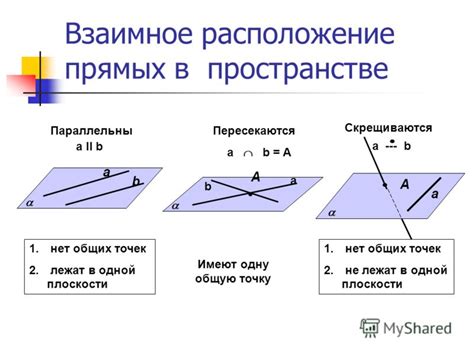
В пространстве прямые могут располагаться по-разному относительно друг друга: они могут быть параллельными, пересекаться или быть скрещивающимися.
• Параллельные прямые - это прямые, которые лежат в одной плоскости, но не пересекаются ни при каком расположении. Они не имеют общих точек и могут быть описаны как лежащие на одной прямой с разными направляющими векторами.
• Пересекающиеся прямые - это прямые, которые имеют одну общую точку. Такие прямые могут иметь разные направляющие векторы, но обязательно пересекаются в одной точке в пространстве.
• Скрещивающиеся прямые - это прямые, которые не параллельны, но также не пересекаются ни при каком расположении. Они могут иметь разные направляющие векторы и лежать в разных плоскостях. Узнать, что прямые скрещивающиеся, можно при помощи косинуса угла между векторами.
Понимание взаимного расположения прямых в пространстве помогает в решении многих геометрических задач, а также играет важную роль в техническом моделировании, архитектуре и других областях, где требуется работать с трехмерными объектами.
Практические примеры и задачи на пересечение прямых
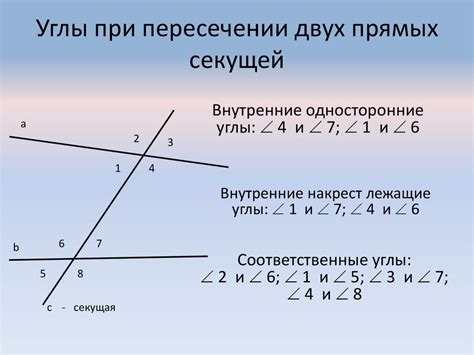
Понимание понятия пересечение прямых необходимо не только для упрощения графической интерпретации геометрических конструкций, но и для решения практических задач, связанных с анализом и моделированием различных явлений и процессов. Ниже представлены несколько примеров и задач, которые помогут лучше освоить эту тему.
Пример 1:
Найти координаты точки пересечения прямых 2x + 3y - 5 = 0 и 3x - 4y + 7 = 0.
| Уравнение прямой | Коэффициенты |
|---|---|
| 2x + 3y - 5 = 0 | a = 2, b = 3, c = -5 |
| 3x - 4y + 7 = 0 | a = 3, b = -4, c = 7 |
Определяем определитель:
D = ab - ba = 2 * (-4) - 3 * 3 = -8 - 9 = -17
Так как определитель не равен нулю, прямые не параллельны и пересекаются в точке. А для нахождения координат точки пересечения можно воспользоваться формулами Крамера:
x = (bc - cb) / D = (3 * (-5) - 3 * 7) / (-17) = (-15 - 21) / -17 = -36 / -17 ≈ 2.12
y = (ac - ca) / D = (2 * 7 - (-5) * 3) / (-17) = (14 + 15) / -17 = 29 / -17 ≈ -1.71
Ответ: Координаты точки пересечения прямых равны примерно (2.12, -1.71).
Пример 2:
Даны уравнения трех плоскостей:
2x + 3y - 4z + 5 = 0
x - 3y + 2z - 7 = 0
4x + 2y + 3z - 1 = 0
Найти точку пересечения этих плоскостей.
| Уравнение плоскости | Коэффициенты |
|---|---|
| 2x + 3y - 4z + 5 = 0 | a = 2, b = 3, c = -4, d = -5 |
| x - 3y + 2z - 7 = 0 | a = 1, b = -3, c = 2, d = 7 |
| 4x + 2y + 3z - 1 = 0 | a = 4, b = 2, c = 3, d = -1 |
Для определения точки пересечения плоскостей составим однородную систему уравнений из коэффициентов плоскостей:
2x + 3y - 4z = -5
x - 3y + 2z = 7
4x + 2y + 3z = 1
Используя метод Гаусса, приведем систему к треугольному виду:
[ 2 3 -4 -5 | 0 ] --> [ 2 3 -4 -5 | 0 ]
[ 1 -3 2 7 | 0 ] --> [ 0 -9 5 17 | 0 ]
[ 4 2 3 1 | 0 ] --> [ 0 -9 5 17 | 0 ]
Теперь приведем систему к диагональному виду:
[ 2 3 -4 -5 | 0 ] --> [ 2 3 -4 -5 | 0 ]
[ 0 -9 5 17 | 0 ] --> [ 0 1 -5.56 -1.89 | 0 ]
[ 0 0 1.67 15.44 | 0 ] --> [ 0 0 1 -9.26 | 0 ]
Получили, что z = -9.26.
Подставляем это значение во второе уравнение и находим y:
y = -1.89 + 5.56z = -1.89 + 5.56 * (-9.26) ≈ -55.51
Подставляем найденные значения в первое уравнение и находим x:
x = (5 + 4z - 3y) / 2 = (5 + 4 * (-9.26) - 3 * (-55.51)) / 2 ≈ 77.62
Ответ: Точка пересечения плоскостей имеет координаты примерно (77.62, -55.51, -9.26).
Задача:
Два поезда одновременно вышли из пунктов А и Б и двигаются навстречу друг другу по параллельным прямым путям. За 8 часов они встретились на расстоянии 960 км от пункта А. Если скорость первого поезда на 20 км/ч меньше скорости второго, найдите скорости каждого поезда.
Решение:
Пусть скорость второго поезда будет равна V км/ч. Тогда скорость первого поезда будет равна V - 20 км/ч. Расстояние между поездами с каждым часом уменьшается на величину равную сумме их скоростей. За 8 часов расстояние между поездами уменьшается на 960 км.
Расстояние = Время * Скорость
960 = 8 * (V + V - 20)
960 = 8 * (2V - 20)
960 = 16V - 160
16V = 960 + 160
16V = 1120
V = 1120 / 16
V = 70
Скорость первого поезда: V - 20 = 70 - 20 = 50 км/ч
Скорость второго поезда: V = 70 км/ч
Ответ: Скорость первого поезда составляет 50 км/ч, а скорость второго - 70 км/ч.



