Дополнительный луч - это понятие, которое используется в геометрии 7-го класса для описания особого типа луча. Лучи - это отрезки, имеющие один фиксированный конец и бесконечно продолжающиеся в противоположном направлении. Дополнительный луч отличается от обычного луча тем, что он имеет общую точку с другим лучом и продолжается в противоположную сторону.
Для понимания дополнительного луча, нужно представить два луча, имеющих общую начальную точку, расположенные на одной прямой. Расширяя эти лучи в противоположном направлении, мы получаем дополнительные лучи. Они имеют общую начальную точку и продолжаются в разные стороны, образуя угол между собой.
Дополнительные лучи могут быть использованы для решения различных задач в геометрии. Например, они могут помочь определить противоположные углы, параллельные и пересекающиеся прямые линии, а также принципы конструкции и измерения углов. Важно понимать, что дополнительные лучи являются вспомогательными геометрическими объектами, которые помогают анализировать и понимать различные геометрические фигуры и свойства.
Определение и основные свойства дополнительного луча
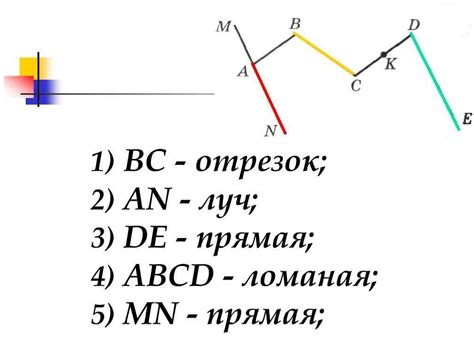
Основные свойства дополнительного луча:
- Дополнительные лучи образуют дополнительный угол, который всегда равен 180 градусам.
- Дополнительные лучи лежат на одной прямой и направлены в противоположные стороны.
- Дополнительные лучи не могут быть параллельными, так как они должны пересекаться в вершине угла.
- Дополнительные лучи могут быть ориентированы в разных направлениях, но вместе они всегда образуют прямую линию.
Дополнительный луч является важным понятием в геометрии, так как он используется для определения и измерения углов. Знание основных свойств дополнительного луча помогает понять геометрические конструкции и решать задачи связанные с углами и их измерением.
Пример:
Допустим, у нас есть два пересекающихся луча с общей вершиной. Образованный ими угол может быть измерен и, согласно свойству дополнительных углов, сумма этого угла и угла, который дополняет его до 180 градусов, также будет равна 180 градусам.
Способы нахождения дополнительного луча

| Способ | Описание |
|---|---|
| Использование угла | Дополнительный луч может быть найден путем измерения угла между начальным лучом и его продолжением. Найденный угол будет равен дополнительному углу, образованному дополнительным лучом. |
| Использование прямой | Дополнительный луч также может быть найден путем продления начального луча до пересечения с другой известной прямой. Точка пересечения будет являться конечной точкой дополнительного луча. |
| Использование геометрических свойств | Дополнительный луч может быть найден путем применения геометрических свойств и теорем. Например, если известно, что начальный и дополнительный лучи являются сторонами угла, то можно использовать свойства углов и сторон для нахождения дополнительного луча. |
Независимо от выбранного метода, нахождение дополнительного луча позволяет расширить известную информацию о геометрической фигуре и отношениях между ее элементами. Это может быть полезным при решении различных геометрических задач и конструировании.
Угол между дополнительным лучом и прямой
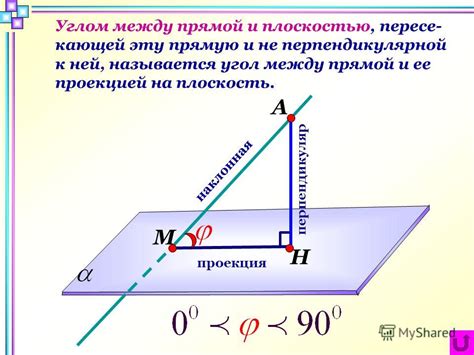
Представим себе, что имеется прямая линия, и на ней выбрана точка. Если от этой точки провести два луча, которые имеют общую вершину и не пересекаются, то их можно рассматривать как два угла. Один из них называется основным углом, а другой - дополнительным углом.
Угол между дополнительным лучом и прямой может быть либо прямым, либо величиной меньше 90°. Это связано с определенными свойствами дополнительных углов.
Если сумма двух углов равна 180°, то они называются смежными углами. В данном случае, основной угол и дополнительный угол являются смежными углами, так как сумма их внутренних углов равна 180°.
Угол между дополнительным лучом и прямой может быть использован при решении различных задач, связанных с геометрией, например, для определения углов между прямыми или для нахождения неизвестных углов в треугольниках и многоугольниках.
Приложения дополнительного луча в геометрии
1. Определение углов
С помощью дополнительного луча можно определить различные виды углов. Например, при наложении дополнительного луча на сторону угла, он делит его на два угла. Таким образом, дополнительный луч помогает определить прямой угол, острый угол, тупой угол и другие виды углов.
2. Классификация отрезков и линий
С помощью дополнительного луча можно классифицировать отрезки и линии. Например, если дополнительный луч пересекает отрезок, то отрезок можно назвать отрезком, а если дополнительный луч пересекает линию, то линию можно назвать прямой.
3. Определение расположения точек
Дополнительный луч помогает определить, находится ли точка на одной стороне отрезка или линии, или на противоположной стороне. Если точка находится на дополнительном луче, то она находится на его продолжении.
4. Решение геометрических задач
Дополнительный луч пригоден для решения различных геометрических задач, например, для построения параллельных и перпендикулярных линий, определения видимой граней при вычислении объемов и площадей геометрических фигур и др.
Таким образом, дополнительный луч является важным инструментом в геометрии, который находит свое применение при классификации углов и линий, определении расположения точек и решении геометрических задач.
Расположение дополнительного луча относительно других лучей
1. Если основной луч и дополнительный луч лежат на одной прямой, то они называются соседними или смежными лучами. В этом случае основной луч и дополнительный луч начинаются из одной точки и направлены в одном направлении.
2. Если основной луч и дополнительный луч не лежат на одной прямой, то они называются неконгруэнтными лучами. В этом случае основной луч и дополнительный луч принимают разные направления и не пересекаются.
3. Если основной луч и дополнительный луч пересекаются, то они называются пересекающимися лучами. В этом случае основной луч и дополнительный луч образуют угол и вместе с этими лучами образуют плоский угол.
Таким образом, расположение дополнительного луча может быть соседним, неконгруэнтным или пересекающимся в зависимости от положения основного луча и сторон угла.
Связь дополнительного луча с другими геометрическими фигурами
- С прямой: дополнительный луч может быть продолжением прямой, если они имеют одно и то же начало и направление. В этом случае он создает бесконечную линию.
- С углом: дополнительный луч может быть одной из сторон угла, с которой он образует угол. Он может быть продолжением стороны или противоположной стороной угла.
- Со сторонами многоугольника: дополнительный луч может быть продолжением одной из сторон многоугольника, если он имеет то же начало и направление. Он также может быть параллельным или пересекать стороны многоугольника.
- С окружностью: дополнительный луч может быть проведен внутри окружности, проходить через ее центр или быть проведенным извне окружности.
Связь дополнительного луча с другими геометрическими фигурами позволяет решать различные задачи и устанавливать свойства этих фигур. Понимая связь между дополнительным лучом и другими элементами, можно легче анализировать и визуализировать геометрические конструкции.
Примеры задач с использованием дополнительного луча

Рассмотрим несколько примеров задач, в которых применяется понятие дополнительного луча в геометрии:
Задача: В треугольнике ABC проведена высота CH, которая пересекает сторону AB в точке D. Докажите, что луч ED является дополнительным лучом к углу BCD.
Решение: По определению, дополнительный луч - это луч, который суммируется с исходным лучом и образует прямую линию. Угол BCD является прямым углом, значит, для того чтобы луч ED был дополнительным к этому углу, он должен быть на прямой линии с лучом BC. Так как луч BC является продолжением стороны AB, то луч ED будет его продолжением. Следовательно, луч ED является дополнительным лучом к углу BCD.
Задача: Найдите значение угла x, если известно, что дополнительный луч дает угол 90°.
Решение: По определению, если угол x и его дополнительный угол в сумме дают 180°, то дополнительный угол будет равен 180° - 90° = 90°. Следовательно, угол x равен 90°.
Задача: В треугольнике ABC проведены высоты AD и BE, пересекающиеся в точке H. Докажите, что угол DHB является дополнительным к углу AHC.
Решение: По определению, дополнительный угол - это угол, который суммируется с исходным углом и образует прямой угол. Угол AHC является прямым углом, следовательно, для того чтобы угол DHB был дополнительным к этому углу, он должен быть на прямой линии с лучами AD и BE. Так как лучи AD и BE являются высотами треугольника, то луч DH будет продолжением луча AD, а луч HB - продолжением луча BE. Таким образом, луч DHB будет лежать на прямой линии с лучами AD и BE, что является условием для дополнительного угла. Следовательно, угол DHB является дополнительным к углу AHC.
Выше приведены лишь некоторые примеры задач, в которых используется понятие дополнительного луча в геометрии. Оно является важным инструментом для доказательства различных геометрических свойств и вычисления значений углов.



