Математическая теория множеств изучает свойства и отношения множеств. Одним из основных понятий в этой теории является операция разности множеств. Но как доказать, что разность двух конечных множеств также является конечным множеством? Для этого необходимо применить логическое рассуждение, основанное на аксиомах множественной алгебры.
Предположим, что у нас есть два конечных множества А и В. Для начала, давайте вспомним, что для конечных множеств выполняется условие, что количество элементов каждого множества можно выразить натуральным числом. Пусть |A| и |B| обозначают количество элементов в каждом множестве соответственно.
Теперь рассмотрим разность множеств А и В. Обозначим эту разность как A \ B. Операция разности заключается в удалении из множества А всех элементов, которые принадлежат множеству В. Если множества А и В имеют конечное число элементов, то каждый элемент множества В можно удалить из множества А ровно один раз.
Таким образом, мы можем утверждать, что разность двух конечных множеств также является конечным множеством. Ведь после удаления конечного числа элементов каждого множества, останется только конечное количество элементов в результате операции разности. Такое рассуждение является строго логическим доказательством того, что разность двух конечных множеств конечна.
Определение конечных множеств
Конечные множества могут состоять из любых элементов: чисел, букв, слов, объектов и т.д. Главное условие - количество элементов в таком множестве должно быть конечным.
Для обозначения конечных множеств используют фигурные скобки {}. Внутри фигурных скобок перечисляют элементы множества через запятую. Например, конечное множество, состоящее из элементов "a", "b" и "c", может быть записано как {a, b, c}.
Конечные множества часто используются в математике, логике и компьютерных науках. Они представляют собой простой и удобный способ описания конкретного количества элементов, что позволяет проводить операции с ними, в том числе находить разность между двумя конечными множествами.
Операция разности множеств

Пусть у нас есть два конечных множества A и B. Разность множеств обозначается как A \ B или A - B и определяется следующим образом:
Для каждого элемента x из множества A, если этот элемент не принадлежит множеству B, он включается в результат.
Иными словами, результатом операции разности множеств будет множество, содержащее только те элементы, которые принадлежат множеству A, но не принадлежат множеству B.
Важно отметить, что разность множеств может быть пустым множеством, если все элементы множества A также принадлежат множеству B. В этом случае разность множеств будет равна пустому множеству.
По определению, конечное множество содержит конечное количество элементов. Поэтому разность двух конечных множеств также будет содержать конечное количество элементов. Таким образом, можно с уверенностью утверждать, что разность двух конечных множеств является конечным множеством.
Доказательство конечности разности множеств

Для доказательства конечности разности двух конечных множеств необходимо рассмотреть каждый элемент множества и установить, что в разности множеств эти элементы будут не повторяться.
Предположим, что у нас есть два конечных множества A и B. Разность множеств A и B обозначается как A \ B. Разность множеств состоит из всех элементов, которые присутствуют в множестве A, но отсутствуют в множестве B.
Предположим, что множество A содержит n элементов, а множество B содержит m элементов. Нам нужно доказать, что разность множеств A \ B содержит конечное количество элементов.
Пусть элементы множества A обозначены как a1, a2, ..., an и элементы множества B обозначены как b1, b2, ..., bm. Тогда разность множеств A \ B можно представить как (a1, a2, ..., an) \ (b1, b2, ..., bm).
Если все элементы множества A уникальны и не повторяются, то в разности множеств A \ B не будет повторений элементов множества A. То есть конечное множество A будет содержать только те элементы, которые отсутствуют в множестве B.
Таким образом, разность множеств A \ B будет состоять из конечного количества элементов из множества A, присутствие которых в нем не зависит от количества элементов множества B. Следовательно, разность двух конечных множеств также будет конечным множеством.
Примеры конечных множеств и их разностей

Рассмотрим несколько примеров конечных множеств и их разностей:
Множество A: {1, 2, 3}
Множество B: {2, 3, 4}
Разность A и B: A - B = {1}
Множество C: {a, b, c, d}
Множество D: {b, c}
Разность C и D: C - D = {a, d}
Множество E: {red, green, blue}
Множество F: {green, yellow}
Разность E и F: E - F = {red, blue}
Как видно из этих примеров, разность двух конечных множеств содержит только те элементы, которые присутствуют в первом множестве, но отсутствуют во втором. Данные примеры подтверждают, что разность двух конечных множеств всегда является конечным множеством.
Связь с другими понятиями в теории множеств

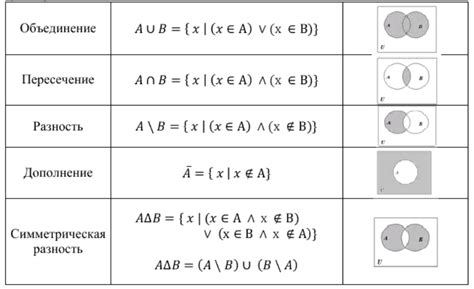
Пересечение множеств – это операция, которая находит общие элементы двух множеств. Как и разность множеств, пересечение может быть применено к конечным множествам. Важно отметить, что разность двух конечных множеств можно представить с помощью пересечения и дополнения – универсального множества.
- Разность множеств можно вычислить как пересечение первого множества с дополнением второго множества.
- То есть, разность множеств A и B может быть записана как A ∩ (U \ B), где U – универсальное множество.
Дополнение множества – это операция, которая находит элементы, принадлежащие универсальному множеству, но не принадлежащие данному множеству. В случае разности двух конечных множеств, дополнение второго множества представляет собой элементы, которые не являются частью разности.
- Таким образом, дополнение второго множества может быть записано как U \ B, где B – второе множество, а U – универсальное множество.
Симметрическая разность – это операция, которая находит элементы, принадлежащие только одному из двух множеств. В случае разности двух конечных множеств, симметрическая разность является объединением разностей двух множеств.
- То есть, симметрическая разность множеств A и B может быть записана как (A \ B) ∪ (B \ A).
Таким образом, разность двух конечных множеств имеет связь с операциями пересечения, дополнения и симметрической разности. Эти операции позволяют вычислить разность множеств, исходя из их общих и уникальных элементов. Они представляют собой важные понятия в теории множеств и широко используются в математике, логике и других областях.
1. Разность двух конечных множеств также является конечным множеством. Для доказательства этого факта достаточно рассмотреть процедуру вычеркивания элементов одного множества из другого. Поскольку изначальные множества содержат лишь конечное число элементов, процесс удаления элементов также будет иметь конечное число шагов. Таким образом, оставшаяся после вычеркивания разность двух конечных множеств будет также конечной.
2. Разность двух конечных множеств может быть пустым множеством. В случае, когда одно множество полностью содержит все элементы другого множества, после вычеркивания останется пустое множество. Это подтверждает факт конечности разности, поскольку пустое множество является конечным по определению.
3. Мощность разности двух конечных множеств может быть меньше мощности одного из исходных множеств. Если одно множество содержит лишь часть элементов другого множества, то после вычеркивания оно становится меньше по размеру. Это также говорит о конечности разности, поскольку мощность множества ограничена числом его элементов.



