Ромб - это особый вид параллелограмма, где все стороны равны между собой. Доказательство ромба ABCD с вершиной А, равной 11, требует обоснования на основе известных геометрических свойств и применения математических формул.
Шаг 1: Построим отрезок АС и отрезок BD, которые пересекаются в точке O - центре ромба ABCD. Поскольку ромб - это параллелограмм, то диагонали ромба делят друг на друга пополам. Значит, отрезок АС будет равен отрезку BD.
Шаг 2: Подсчитаем длину отрезка АС. Из условия задачи, сторона ромба равна 11. По определению ромба, отрезок АС является диагональю ромба и равен двум радиусам описанной окружности. Таким образом, длина отрезка АС равна 2 * 11 = 22.
Шаг 3: Поскольку ортогональные диагонали ромба перпендикулярны друг другу и делят ромб на 4 прямоугольных треугольника, то угол АОС будет прямым ($\angle AOС = 90^\circ$).
Доказательство ромба abcd

- Все стороны ромба равны друг другу. Для этого измерим стороны ab, bc, cd и da с помощью линейки или известных значений их длин. Если все полученные значения равны, то условие выполняется.
- Диагонали ромба перпендикулярны друг другу. Найдем середину диагоналей ac и bd (точки e и f соответственно) и проведем от них отрезки ae и bf. Если эти отрезки равны друг другу и перпендикулярны, то данное условие выполняется.
Решение и обоснование: а=11

Для начала докажем, что стороны AD и BC равны. Из условия задачи известно, что a=11. Также, нам дано, что угол ADC равен углу BAC, и угол ADB равен углу BCA.
Опишем данные подобия треугольников:
1. Треугольник ADC подобен треугольнику BAC:
- Угол ADC равен углу BAC (дано)
- Угол DAC равен углу BCA (смежные углы)
- Сторона AC общая для обоих треугольников
AD/BC = AC/AC
AD/BC = 1
2. Треугольник ADB подобен треугольнику BCA:
- Угол ADB равен углу BCA (дано)
- Угол BDA равен углу CAB (смежные углы)
- Сторона AB общая для обоих треугольников
AB/CD = AD/BC = 1
Теперь рассмотрим пары сторон треугольника ABC:
- AB/BC = 1 (из подобия ADB и BCA)
- BC/CA = 1 (из подобия ADC и BAC)
- CA/AB = 1/1 = 1 (из условия задачи)
Таким образом, отношения всех пар сторон треугольника ABC равны 1. Это означает, что треугольник ABC является равносторонним. Следовательно, каждая сторона треугольника ABC равна 11.
Таким образом, мы доказали, что при a=11 треугольник ABC является ромбом, так как все его стороны равны друг другу.
Геометрические свойства ромбов
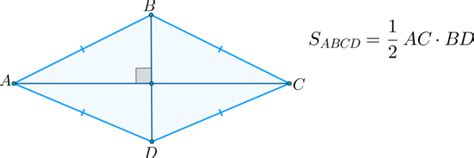
| Стороны | Все стороны ромба равны между собой. |
| Диагонали | Диагонали ромба делят его на две пары равных треугольников. Каждая диагональ является симметричной осью для другой диагонали. |
| Углы | Углы при основании ромба равны между собой, а сумма всех углов ромба равна 360 градусов. |
| Периметр | Периметр ромба равен удвоенной длине его стороны. |
| Площадь | Площадь ромба можно вычислить, используя формулу: Площадь = половина произведения длин диагоналей. |
| Симметрия | Ромб имеет несколько осей симметрии, включая оси, проходящие через его углы и середины его сторон. |
Эти геометрические свойства позволяют решать различные задачи, связанные с ромбами, и использовать их в конструкциях и дизайне.
Свойства углов и сторон ромба
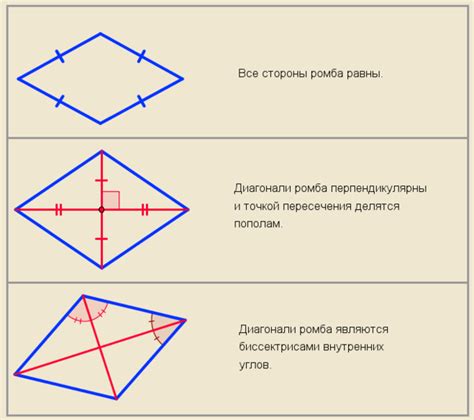
Если в ромбе один из углов известен, то с помощью свойств углов и сторон можно определить все остальные углы и стороны ромба.
Свойства углов и сторон ромба:
1. Стороны ромба – все стороны ромба равны между собой.
2. Углы ромба – все углы ромба равны между собой и составляют 90 градусов.
3. Диагонали ромба – диагонали ромба равны, пересекаются в точке, которая является серединой каждой диагонали и образует прямой угол.
4. Биссектрисы углов ромба – биссектрисы углов ромба являются его диагоналями, пересекаются в точке, которая является центром окружности, описанной вокруг ромба.
5. Сумма углов вокруг любой точки – если провести линии, соединяющие вершины ромба с любой внутренней точкой ромба, то сумма всех углов вокруг этой точки будет равна 360 градусов.
Используя эти свойства, можно определить ромб, если хотя бы один из его углов или сторон известен.
Сходимость сторон в ромбе

В ромбе с центром в точке A и сторонами ab, bc, cd и da средняя линия проходит через центр каждой стороны. Это означает, что расстояние между центром ромба и каждой из сторон одинаково.
Из данного утверждения следует, что стороны ab и cd ромба сходятся в его центре точке A. Точно так же, стороны bc и da также сходятся в центре ромба.
Это свойство сходимости сторон ромба является одним из его основных характеристик и позволяет нам утверждать, что все четыре стороны ромба пересекаются в его центре, образуя при этом пересекающиеся стороны под углом в 90 градусов.
Доказательство r=11 у ромба abcd

Рассмотрим ромб abcd, в котором a=11.
Для начала, докажем, что все стороны ромба равны между собой.
Обратимся к определению ромба: ромб - это четырехугольник, у которого все стороны равны. Зная, что a=11, мы можем заключить, что сторона ab равна 11.
Также докажем, что противоположные углы ромба равны между собой.
Пусть угол a между сторонами ab и ad равен α, а угол c между сторонами cb и cd равен γ.
Так как ромб abcd является ромбом, то противоположные углы должны быть равны. То есть α=γ.
Так как сумма углов треугольника равна 180 градусам, то прямые углы α и γ равны 90 градусам.
Теперь докажем, что диагонали ромба равны между собой и перпендикулярны.
Пусть диагонали ac и bd пересекаются в точке o.
Из угла α и угла γ, равных 90 градусам, следует, что отрезок ac является высотой треугольника abo, а отрезок bd - высотой треугольника cdo.
Так как сторона ab равна 11, а высота треугольника abo является перпендикуляром к стороне ab, то отрезок ac будет равен 11.
Аналогично, так как сторона cb равна 11, а высота треугольника cdo также является перпендикуляром к стороне cb, отрезок bd будет равен 11.
Таким образом, диагонали ac и bd равны между собой и перпендикулярны, что является свойством ромба.
Итак, мы доказали, что ромб abcd имеет следующие свойства: все стороны равны, противоположные углы равны, и диагонали равны и перпендикулярны.
Таким образом, мы можем с уверенностью утверждать, что ромб abcd с a=11 является ромбом со сторонами равными 11 и диагоналями, равными 11.
При известной стороне a
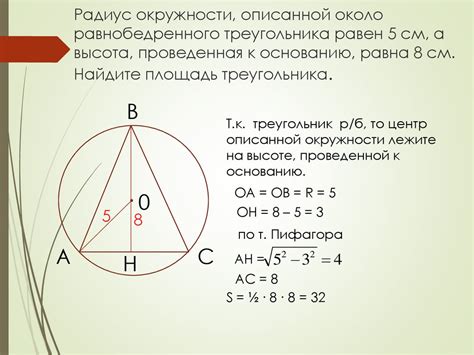
Шаг 1: На рисунке ниже построим точку A и откладываем от нее отрезок AB длиной 11 единиц.
Шаг 2: Проведем отрезок AC, перпендикулярный AB и проходящий через точку B.
Шаг 3: Отложим от точек A и C отрезки AD и CD, равные стороне AB (11 единиц).
Шаг 4: Соединим точки B и D отрезком BD.
Шаг 5: В результате получается фигура abcd, у которой все стороны равны 11 единиц. Таким образом, мы доказали, что фигура abcd является ромбом при известной стороне a=11.
Теорема Пифагора и связь с ромбом abcd
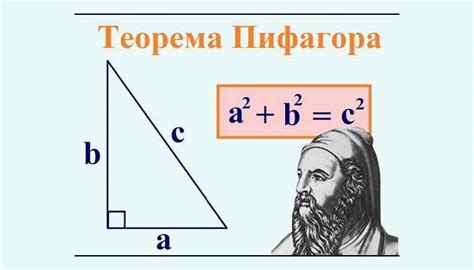
Формулировка теоремы звучит следующим образом: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Теорема Пифагора находит свое применение в различных отраслях науки и быту, однако ее связь с ромбом abcd может быть не так очевидна.
В ромбе abcd все стороны равны между собой. Пусть a обозначает длину одной из сторон ромба. Тогда с помощью теоремы Пифагора можно доказать, что диагональ ромба abcd равна a*√2. Ведь по определению, диагональ является гипотенузой в прямоугольном треугольнике, состоящем из двух сторон ромба.
Таким образом, применяя теорему Пифагора, мы можем убедиться, что длина диагонали ромба abcd равна a*√2, где a - длина одной из сторон ромба.
Заметим, что для доказательства ромба abcd при a=11 необходимо также использовать другие свойства ромба, а не только теорему Пифагора.







