В математике одной из важнейших задач является определение взаимной простоты двух чисел. Взаимная простота двух чисел означает, что они не имеют общих делителей, кроме 1. Такая характеристика является важным условием для многих математических и инженерных задач.
Давайте рассмотрим числа 468 и 875 и проверим, являются ли они взаимно простыми. Первым шагом в решении этой задачи является разложение каждого числа на простые множители.
Число 468 можно разложить на простые множители следующим образом: 2 * 2 * 3 * 3 * 13. А число 875 разложим как 5 * 5 * 5 * 7. Теперь мы можем сравнить простые множители обоих чисел.
Определение и особенности простых чисел
Главная особенность простых чисел заключается в том, что они не могут быть представлены как произведение других чисел, отличных от 1 и самого числа. Это означает, что простые числа являются основными строительными блоками для всех остальных чисел, поскольку любое число может быть раскладено на простые множители.
Важно отметить, что существует бесконечное количество простых чисел. Это связано с тем, что если бы было конечное число простых чисел, то можно было бы найти самое большое простое число и умножить его на все другие простые числа, получив таким образом новое простое число, что противоречит исходному предположению о наличии конечного числа простых чисел.
Простые числа играют важную роль в различных областях математики и криптографии. Они используются для построения криптографических алгоритмов, защищающих информацию от несанкционированного доступа.
Теорема о невзаимной простоте

Теорема о невзаимной простоте утверждает, что если два числа не имеют общих делителей, то они называются взаимнопростыми или невзаимно простыми. Другими словами, если наибольший общий делитель (НОД) двух чисел равен единице, то числа считаются взаимнопростыми.
Доказательство этой теоремы состоит в приведении рассуждений, основываясь на свойствах НОД и делителей.
Пусть у нас есть два числа a и b, и их НОД равен единице. Предположим, что у нас есть общий делитель c, который не равен единице. Тогда c делит и a, и b. Но если c делит и a, и b, то он также должен делить и их разность (a - b), так как (a - b) = q * c, где q - целое число. Итак, мы получаем, что c делит и (a - b).
Разложение чисел на простые множители

Для разложения числа на простые множители можно использовать разные методы, включая перебор делителей и применение алгоритмов. Начиная с наименьшего простого числа, мы делим исходное число на эти числа до тех пор, пока не получим простое число в результате деления или пока число не станет равным единице. Получившееся произведение простых множителей и будет разложением исходного числа на простые множители.
Например, число 468 можно разложить на простые множители 2 и 3: 468 = 2 * 2 * 3 * 3 * 13. А число 875 разлагается на множители 5 и 7: 875 = 5 * 5 * 5 * 7.
Разложение чисел на простые множители важно в различных областях математики и находит применение, например, в теории чисел, алгебре и криптографии. Это позволяет анализировать свойства чисел и выполнять различные арифметические операции, а также решать задачи с использованием общих факторов чисел.
Важно: взаимная простота чисел означает, что эти числа не имеют общих простых множителей, то есть их разложения на простые множители не имеют общих простых множителей.
Доказательство взаимной простоты числа 468

Чтобы доказать взаимную простоту числа 468 с другим числом, нужно проверить их общие простые делители. Очевидно, что число 468 делится на 2 без остатка, так как оно четное. Поэтому число 468 не взаимно просто ни с одним другим четным числом, включая число 875.
Таким образом, числа 468 и 875 не являются взаимно простыми числами, поскольку они имеют общий делитель - число 2.
Доказательство взаимной простоты числа 875
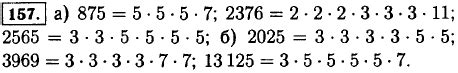
Число 875 разлагается на простые множители: 5 * 5 * 5 * 7. Заметим, что числа 5 и 7 являются простыми числами, и они не делятся нацело на 468.
Таким образом, нет общих делителей у чисел 875 и 468, кроме единицы. Значит, число 875 является взаимно простым с числом 468.
Сравнение разложений на простые множители

В нашем случае, число 468 может быть разложено на простые множители как 2 * 2 * 3 * 3 * 13, а число 875 - как 5 * 5 * 5 * 7.
Сравнивая разложения на простые множители, мы можем установить, что в обоих случаях отсутствуют общие простые множители. Таким образом, числа 468 и 875 являются взаимно простыми.
| Число | Разложение на простые множители |
|---|---|
| 468 | 2 * 2 * 3 * 3 * 13 |
| 875 | 5 * 5 * 5 * 7 |



