Трапеция - это многоугольник, у которого две противоположные стороны параллельны. Одна из особенностей трапеции заключается в том, что углы при ее основаниях равны друг другу. Данное утверждение является одним из основных свойств трапеции и может быть доказано с помощью геометрических построений и рассуждений.
Для начала рассмотрим трапецию ABCD, где AB и CD - основания, а BC и AD - боковые стороны. Рассмотрим углы A и D, расположенные у оснований. Чтобы доказать их равенство, построим параллельную прямую EF к основаниям трапеции.
Так как AB и CD параллельны, то прямая EF также является параллельной этим основаниям и перпендикулярной боковой стороне BC. Обозначим точки пересечения прямой EF с боковой стороной BC и основаниями AB и CD соответственно как G, H и I. Из свойства параллельных прямых следует, что углы BGC и BAC равны, так как они являются соответственными.
Также, так как прямые BC и FD перпендикулярны, то углы BGC и FGD, а также угол ABC, образованный прямыми BC и AG, равны. Из равенства углов BGC и FGD следует, что угол A и угол D также равны между собой.
Равенство углов в трапеции
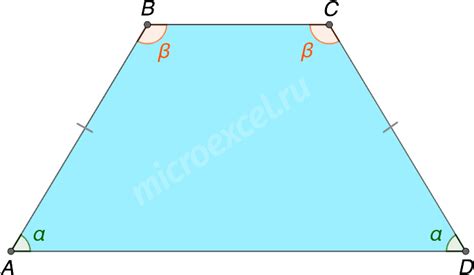
В трапеции с основаниями AB и CD углы при основании равны. Это свойство позволяет утверждать, что две пары углов, образованных диагоналями трапеции и ее основаниями, также равны друг другу.
Докажем данное равенство углов. Рассмотрим трапецию ABCD, где AB и CD - основания, а AC и BD - диагонали.
Из свойств трапеции, мы знаем, что противоположные стороны параллельны, т.е. AB



