Трапеция - это четырехугольник, у которого две стороны параллельны, а две другие - нет. Одно из свойств трапеции заключается в том, что напротив параллельных сторон лежат равные по длине отрезки. В данной статье мы будем рассматривать особый случай трапеции - когда одна из параллельных сторон является основанием, а другая - боковой стороной.
На первый взгляд может показаться, что площади треугольников внутри трапеции не могут быть равными. Однако, существует доказательство этого факта. Давайте рассмотрим трапецию ABCD, где AB - основание, а CD - боковая сторона.
Пусть точка M - середина боковой стороны CD, а точка N - точка пересечения диагоналей AC и BD. Из свойств трапеции следует, что точка N лежит на серединном перпендикуляре к основанию AB, а точка M лежит на серединном перпендикуляре к боковой стороне CD. Заметим, что треугольники ANC и BMD являются подобными, так как углы CAN и BDM прямые.
Свойства трапеции
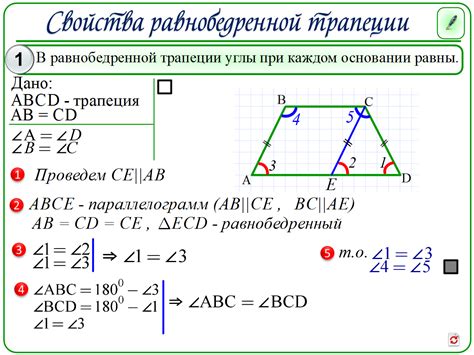
В трапеции две противоположные стороны (боковые стороны) являются параллельными. Это означает, что длина одной боковой стороны равна длине противоположной боковой стороны.
2. Вершины трапеции лежат на одной прямой
Вершины трапеции A, B, C и D лежат на одной прямой, называемой основанием, которая может быть горизонтальной или наклонной.
3. Базы трапеции
Базы трапеции - это две параллельные стороны, которые не являются основаниями. Одна из баз обычно называется верхней базой, а другая - нижней базой.
4. Углы трапеции
Углы трапеции могут быть прямыми углами, острыми углами или тупыми углами. Сумма прямых углов в трапеции всегда равна 180 градусам.
5. Высота трапеции
Высота трапеции - это перпендикуляр, опущенный из одной вершины трапеции на основание или его продолжение. Высота может находиться внутри трапеции или за ее пределами.
Что такое трапеция?
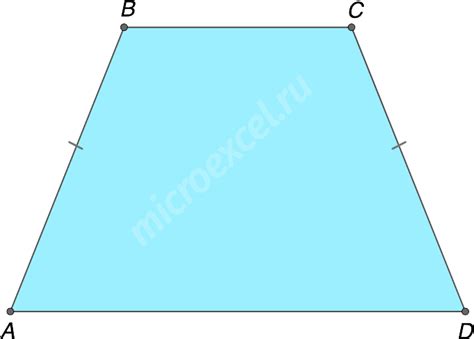
Трапеция может быть исходной фигурой, на основе которой можно строить другие геометрические фигуры, такие как прямоугольник, параллелограмм или ромб.
Другие свойства трапеции включают следующее:
- Трапеция имеет два угла, сумма которых равна 180 градусам.
- Диагонали трапеции не являются равными.
- Углы, образованные диагоналями и основаниями, равны.
Знание свойств трапеции позволяет проводить различные геометрические рассуждения и доказывать равенства площадей треугольников внутри нее.
Особенности трапеции
1. Боковые стороны. В трапеции боковые стороны не параллельны, причем одна из них всегда длиннее другой. Однако, параллельными являются верхняя и нижняя стороны, которые называются основаниями трапеции.
2. Углы. В трапеции существуют особые соотношения между ее углами. Углы при основаниях трапеции являются противоположными, то есть лежат на противоположных сторонах трапеции, но расположены между основаниями. Углы с одной и той же вершиной находятся по разные стороны от параллельных сторон трапеции и называются нижними и верхними осевыми углами.
3. Высота. Высотой трапеции называется отрезок, проведенный перпендикулярно между основаниями. Особенностью высоты трапеции является то, что она равна расстоянию между основаниями. Это свойство позволяет использовать высоту для нахождения площади трапеции.
Трапеция – это простая, но интересная геометрическая фигура, имеющая ряд особенностей, которые могут быть использованы при решении различных задач и доказательств в геометрии.
Площадь трапеции
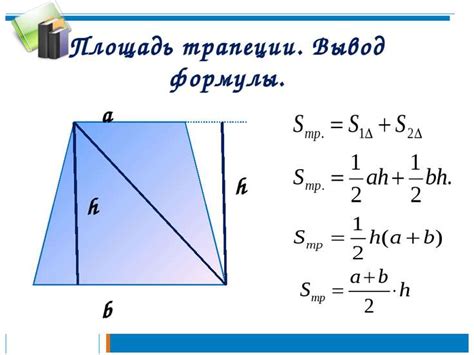
Площадь трапеции вычисляется по формуле:
S = ((a + b) * h) / 2
где:
- a и b - основания трапеции
- h - высота трапеции
Для нахождения площади трапеции необходимо знать длины оснований и высоту. Основания трапеции - это параллельные отрезки, один из которых называется верхним основанием, а другой - нижним основанием. Высота трапеции - это перпендикуляр, опущенный на нижнее основание и проведенный из верхней вершины.
Зная длины оснований трапеции и высоту, можно легко вычислить её площадь по данной формуле.
Формула для вычисления площади
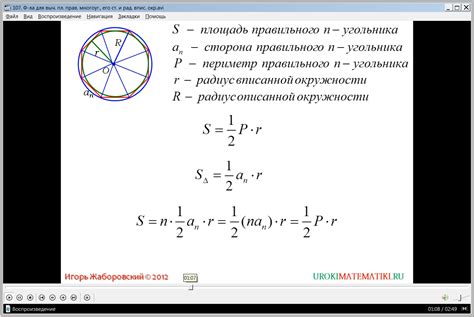
Для вычисления площади треугольника можно использовать простую формулу:
Площадь треугольника = (основание × высота) ÷ 2
Где:
- Основание - это одна из сторон треугольника, которая лежит на основании трапеции. Его длина обозначается символом "a".
- Высота - это расстояние между основанием и противоположным ему углом треугольника. Ее обозначение - символом "h".
Таким образом, зная длину основания и высоту треугольника, можно легко вычислить его площадь, используя приведенную формулу.
Данная формула основана на том факте, что площадь треугольника равна половине площади прямоугольника, у которого высота равна высоте треугольника, а основание равно основанию треугольника.
Эта формула позволяет эффективно вычислять площади треугольников, что важно при решении задач, связанных с геометрией и трапециями.
Доказательство равенства площадей
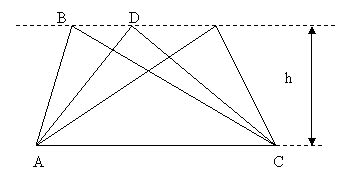
Доказательство равенства площадей треугольников в трапеции основано на свойствах параллельных линий и треугольников.
Для начала, рассмотрим трапецию ABCD, где AB и CD - параллельные стороны, а BC и AD - непараллельные стороны.
Возьмем точки E и F на стороне BC и AD соответственно таким образом, что отрезок EF параллелен боковым сторонам AB и CD.
Также, проведем отрезок GH, который будет параллелен сторонам BC и AD и проходить через середину стороны EF.
Полученные треугольники EGF и GHF будут одинаковыми, так как у них равны боковые стороны и углы.
Теперь рассмотрим площади треугольников ABC, ADE и BCF.
Площадь треугольника ABC равна половине произведения длин оснований AB и CD, так как это свойство трапеции.
Площадь треугольника ADE равняется половине произведения длины основания AD и высоты, опущенной на это основание.
Площадь треугольника BCF также равна половине произведения длины основания BC и высоты, опущенной на это основание.
Так как основание AB равно основанию CD, а высоты, опущенные на основания AD и BC равны между собой (так как GH проходит через середину EF), то площади треугольников ABC, ADE и BCF также равны между собой.
Таким образом, доказано равенство площадей треугольников в трапеции ABCD.
Примеры применения

Доказательство равенства площадей треугольников в трапеции может быть полезным при решении различных геометрических задач. Рассмотрим несколько примеров применения данного доказательства.
Пример 1:
Необходимо найти площадь треугольника, образованного диагоналями трапеции.
Решение: в соответствии с доказательством, площадь треугольника, образованного диагоналями трапеции, равна половине площади самой трапеции. Поэтому достаточно найти площадь трапеции и разделить её на 2.
Пример 2:
Дана трапеция, в которой известны длины всех сторон. Требуется найти площадь треугольника, образованного биссектрисой угла между боковыми сторонами.
Решение: сначала найдем меру угла между боковыми сторонами. Далее, используя формулу площади треугольника через стороны и углы, найдем площадь треугольника. Однако, при наличии доказательства равенства площадей треугольников в трапеции, можно просто найти площадь всей трапеции и разделить её на 2.
Такие примеры применения доказательства равенства площадей треугольников в трапеции позволяют упростить решение геометрических задач, связанных с треугольниками и трапециями.
Задача на вычисление площади треугольников

Для вычисления площади треугольника необходимо знать длины его сторон или другие характеристики, такие как высота, радиус вписанной окружности и т.д.
Если известны длины всех трех сторон треугольника, то для вычисления его площади можно использовать формулу Герона.
Формула Герона:
S = sqrt(p * (p - a) * (p - b) * (p - c))
где a, b и c - длины сторон треугольника, а p - полупериметр, вычисляемый по формуле p = (a + b + c) / 2.
Используя эту формулу, можно вычислить площади треугольников, зная длины всех их сторон.
Важно помнить, что для вычисления площадей треугольников в других случаях, например, когда известна высота или радиус вписанной окружности, следует использовать другие формулы.
Вычисление площади треугольников является важным элементом в решении различных геометрических задач и нахожении равенств площадей в трапеции.



