Введение

Равенство треугольников – это основное свойство геометрии, которое позволяет сравнивать и классифицировать различные треугольники. В данной статье мы рассмотрим доказательство равенства треугольников АВД и АСД и выведем необходимые условия для их равенства.
Доказательство
Предположим, что у нас есть треугольник АВД и треугольник АСД. Чтобы доказать их равенство, нам необходимо показать, что все их стороны и углы равны друг другу.
- Строим сторону АВ, затем проводим прямую, параллельную стороне АС, проходящую через точку D. Обозначим точку пересечения этой прямой с прямой СВ как Е.
- Используя теорему Фалеса, доказываем, что отрезок ЕВ делит сторону АС пополам.
- Также, используя теорему Фалеса, доказываем, что отрезок ЕД делит сторону АВ пополам.
- Из предыдущих шагов следует, что стороны АВ и АС равны, так как они разделены точкой Е на две равные части.
- Далее, доказываем, что углы АВД и АСД равны друг другу. Для этого мы можем использовать аксиому о равенстве углов, говорящую о том, что две пары углов равны, если их стороны параллельны и пересекаются.
- Так как сторона ВЕ параллельна стороне АС и пересекает сторону АД в точке D, мы можем доказать равенство углов АВД и АСД.
Заключение
Таким образом, построив прямую, параллельную одной из сторон и проходящую через вершину, мы доказали равенство треугольников АВД и АСД. Используя теорему Фалеса и аксиому о равенстве углов, мы получили необходимые условия для равенства треугольников. Это доказательство является фундаментальным в геометрии и находит широкое применение в различных математических и инженерных задачах.
Геометрические построения
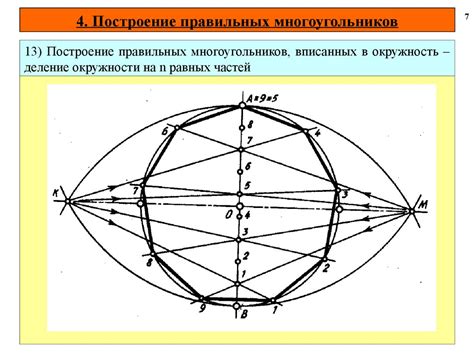
Геометрические построения проводятся с использованием геометрических инструментов, таких как линейка и циркуль. С их помощью можно проводить прямые, отрезки, углы, окружности и многое другое.
Одним из наиболее распространенных геометрических построений является построение серединного перпендикуляра к отрезку. Для этого нужно нарисовать два окружности с радиусом, равным половине длины отрезка, с центрами в его концах. Затем проводится линия, соединяющая центры окружностей, которая и будет серединным перпендикуляром к данному отрезку.
Геометрические построения активно используются при доказывании различных геометрических теорем, таких как теорема Пифагора или равенство треугольников. Используя геометрические построения, можно визуализировать и понять различные геометрические свойства и законы.
Важно помнить, что геометрические построения являются абстрактным представлением объектов и фигур и не всегда могут быть точно воспроизведены на плоскости.
Тщательное выполнение геометрических построений позволяет проводить точные измерения и сравнения различных фигур и объектов, что является неотъемлемой частью геометрии и многих других наук.



