Подобие треугольников – одно из основных понятий в геометрии, которое позволяет сравнить их формы и размеры без учета их абсолютных значений. Доказательство подобия треугольников АВС и А1В1С1 является важным шагом в решении задач, связанных с изучением их свойств и применением в различных областях науки и техники.
Для доказательства подобия треугольников АВС и А1В1С1 используются несколько способов, одним из которых является определение соответствующих сторон и углов. Предположим, что треугольник АВС и треугольник А1В1С1 имеют соответствующие стороны, длины которых обозначены как АВ=A1В1, ВС=В1С1 и СА=С1А1. А также соответствующие углы, которые обозначены как ∠АА1=∠ВВ1=∠СС1.
Следующим шагом является проверка, что пропорциональность соответствующих сторон треугольников совпадает:
АВ / А1В1 = ВС / В1С1 = СА / С1А1
Что такое доказательство подобия треугольников?
Доказательство подобия треугольников часто применяется в геометрии для нахождения неизвестных сторон или углов треугольников. Если известны соответствующие стороны или углы двух треугольников, то можно установить их подобие и использовать пропорциональные отношения для нахождения значений неизвестных величин.
Доказательство подобия треугольников основывается на нескольких свойствах и теоремах. Одно из таких свойств – это равенство углов между соответствующими сторонами треугольников. Если углы между двумя соответствующими сторонами треугольников равны, то треугольники подобны.
Другое свойство, используемое при доказательстве подобия треугольников, – это пропорциональность сторон треугольников. Если отношения длин соответствующих сторон двух треугольников равны, то треугольники подобны. Это позволяет использовать пропорции для нахождения значений неизвестных сторон треугольников.
Доказательство подобия треугольников имеет много практических применений. Оно используется в геодезии, архитектуре, строительстве, визуальных эффектах в киноиндустрии и других областях. Понимание и умение проводить доказательство подобия треугольников позволяет решать сложные задачи и достигать точных результатов.
| Свойства подобных треугольников | Доказательства |
|---|---|
| Углы между соответствующими сторонами подобных треугольников равны | Теорема об угле между параллельными прямыми |
| Длины соответствующих сторон подобных треугольников пропорциональны | Теорема о прямых линиях |
| Размеры и формы подобных треугольников связаны | Теорема о подобии треугольников |
Определение подобности треугольников.
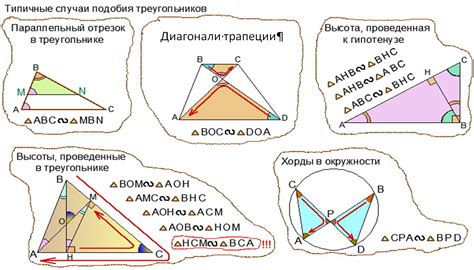
1. Соответствие углов
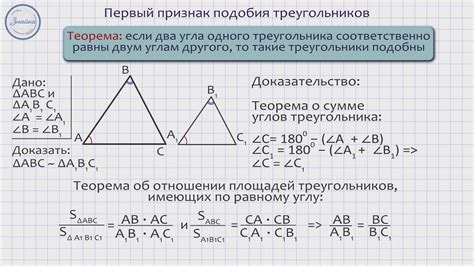
Два треугольника подобны, если их соответствующие углы равны или одинаковые по мере. То есть, угол А равен углу А1, угол В равен углу В1 и угол С равен углу С1. При этом, порядок следования букв A, B, C и A1, B1, C1 не имеет значения.
2. Соответствие сторон
Два треугольника подобны, если их соответствующие стороны пропорциональны. То есть, отношение длины стороны А к стороне А1 равно отношению длины стороны В к стороне В1, и отношение длины стороны В к стороне В1 равно отношению длины стороны С к стороне С1. Это можно записать как:
AB / A1B1 = BC / B1C1 = AC / A1C1
3. Соответствие сторон и углов
Если выполнены условия соответствия углов и соответствия сторон, то треугольники подобны.
Используя эти условия, можно доказать подобие треугольников АВС и А1В1С1 и применять его для решения задач и построения геометрических фигур.
Доказательство подобия треугольников на основе соответствующих сторон
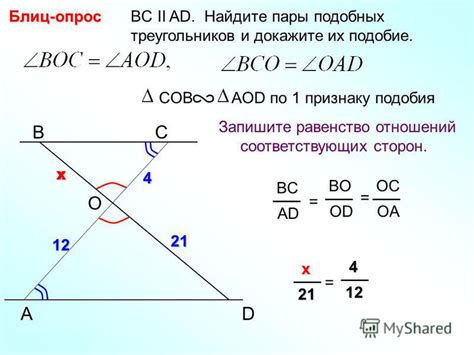
Доказательство подобия треугольников основано на сравнении и соответствии их сторон. Две фигуры называются подобными, если соответствующие углы равны, а отношение длин соответствующих сторон одинаково.
Итак, для доказательства подобия треугольников АВС и А1В1С1 на основе соответствующих сторон, необходимо проверить два условия:
1) Соответствующие углы треугольников равны. Для этого можно воспользоваться свойством треугольника: сумма углов треугольника равна 180 градусов. Сравнивая углы А и А1, B и B1, C и C1, можно убедиться, что соответствующие углы равны.
2) Отношение длин соответствующих сторон одинаково. Для этого необходимо сравнить длины сторон треугольников. Используя теорему Пифагора или другие методы, можно вычислить длины сторон АВ, ВС и СА, а также сторон А1В1, В1С1 и С1А1. Затем сравниваются эти отношения: AB/A1B1, BC/B1C1 и CA/C1A1. Если отношения сторон совпадают, то треугольники подобны по соответствующим сторонам.
Таким образом, доказательство подобия треугольников АВС и А1В1С1 на основе соответствующих сторон осуществляется сравнением углов и отношениями длин сторон. Если оба условия выполняются, то треугольники можно считать подобными.
Доказательство подобия треугольников на основе соответствующих углов

Пусть даны треугольник АВС и треугольник А1В1С1. Для доказательства подобия треугольников на основе соответствующих углов необходимо проверить, что углы треугольника АВС равны соответствующим углам треугольника А1В1С1. Для этого можно использовать таблицу:
| Треугольник АВС | Треугольник А1В1С1 |
|---|---|
| Угол А | Угол А1 |
| Угол В | Угол В1 |
| Угол С | Угол С1 |
Если все углы одного треугольника соответственно равны углам другого треугольника, то треугольники АВС и А1В1С1 подобны.
Доказательство подобия треугольников на основе соответствующих углов является одним из основных методов для определения подобия треугольников. Оно позволяет установить подобие треугольников без измерения сторон или проведения дополнительных построений.
Доказательство подобия треугольников на основе соответствующих сторон и углов

Для доказательства подобия треугольников на основе соответствующих сторон и углов можно использовать несколько методов:
1. Метод коэффициентов подобия При данном методе сравниваются соотношения длин сторон треугольников. Если все стороны двух треугольников имеют равные соотношения, то треугольники подобны. | 2. Метод углов Данный метод основан на сравнении углов треугольников. Если углы двух треугольников равны или соответственно пропорциональны, то треугольники подобны. |
3. Метод параметров Данный метод основан на сравнении параметров треугольников, таких как площадь, периметр, радиус описанной окружности и другие. Если данные параметры двух треугольников равны или соответствуют друг другу, то треугольники подобны. | 4. Метод пропорциональности Этот метод заключается в сравнении пропорциональности сторон и углов треугольников. Если стороны и углы двух треугольников соответственно пропорциональны, то треугольники подобны. |
Все указанные методы позволяют доказать подобие треугольников на основе соответствующих сторон и углов. Они представляют собой важный инструмент для решения задач геометрии и нахождения неизвестных значений в подобных треугольниках.
Применение доказательства подобия треугольников в практике

Одна из основных практических областей, где применяется доказательство подобия треугольников, – это геодезия и картография. С помощью этого понятия можно строить карты и планы местности, определять расстояния между объектами и измерять их размеры. Например, зная высоту солнца и длину его тени, можно определить высоту любого предмета, используя принципы подобия треугольников.
Доказательство подобия треугольников также применяется в архитектуре и строительстве. Зная размеры одного объекта, можно определить размеры другого подобного объекта. Это позволяет строить здания, мосты и сооружения, соответствующие заданным пропорциям и требованиям.
В медицине доказательство подобия треугольников используется для определения размеров и формы внутренних органов, при рентгенологических исследованиях и томографии. Это позволяет врачам получить точные данные о состоянии пациента и принять правильное решение по поводу дальнейшего лечения.
Подобное доказательство треугольников находит применение даже в электронике и фотографии. Например, в оптических системах чтобы получить изображение, соответствующее форме и размеру объекта, применяется подобие треугольников. Это помогает создавать точные микросхемы и объективы для камеры, позволяющие получить качественные и детализированные фотографии.
Таким образом, доказательство подобия треугольников имеет практическое применение в различных областях науки и техники. Знание этого понятия позволяет решать различные задачи и получать точные данные о форме и размерах объектов.



