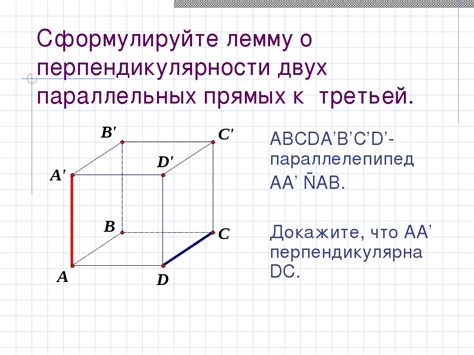
Перпендикуляр – одно из основных понятий геометрии, которое используется для описания взаимного расположения прямых и плоскостей. В данной статье рассмотрим доказательство перпендикулярности отрезка dc, который является диагональю параллелепипеда abcda1b1c1d1.
В начале необходимо вспомнить определение перпендикулярности. Две прямые (или плоскости) называются перпендикулярными, если они пересекаются под прямым углом, то есть угол между ними составляет 90 градусов. В случае параллелепипеда это означает, что отрезок dc должен быть перпендикулярен плоскости, в которой он лежит.
Докажем перпендикулярность отрезка dc при помощи прямых углов. Рассмотрим одну из граней параллелепипеда, например, грань abc. Проведем диагональ от вершины a к вершине c и обозначим ее отрезком ac. Затем проведем вспомогательную прямую bd, которая будет пересекать отрезок ac в точке e. Таким образом, получаем пересечение двух прямых ae и bd в точке e.
Основная идея доказательства заключается в том, что если мы докажем, что углы aeb и ced равны 90 градусов, то это будет означать перпендикулярность отрезка dc плоскости abc. Убедимся в этом. Поскольку отрезок dc является диагональю параллелепипеда, то отрезки ac и bd равны между собой. А так как отрезок ac является диагональю грани abc, то угол aeb также равен 90 градусам. Осталось лишь доказать, что угол ced также равен 90 градусам.
Изучение перпендикулярности отрезка dc в параллелепипеде abcda1b1c1d1
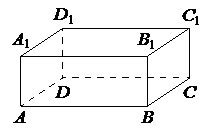
Вначале проведем анализ свойств параллелепипеда abcda1b1c1d1. Параллелепипед является трехмерным объемным телом, у которого противоположные грани параллельны и равны. Каждая грань представляет собой параллелограмм. Отрезок dc - это одна из диагоналей параллелепипеда, проходящая через противоположные вершины.
Далее, мы должны рассмотреть векторные операции. Вектор - это математический объект, который имеет направление и длину. Вектор может быть представлен с помощью координат или с помощью начальной и конечной точек. Сложение векторов осуществляется покомпонентно, а скалярное произведение векторов позволяет определить их перпендикулярность.
Для доказательства перпендикулярности отрезка dc мы можем воспользоваться свойствами параллелепипеда и векторными операциями. Перпендикулярность отрезка dc будет доказана, если скалярное произведение его направляющего вектора и направляющего вектора диагонали, проходящей через противоположные вершины, равно нулю.
Определение и свойства параллелепипеда
У параллелепипеда есть несколько свойств:
- Равенство диагоналей: Диагонали параллелепипеда равны между собой и пересекаются в точке, которую делим на две равные части.
- Перпендикулярные грани: Противоположные грани параллелепипеда перпендикулярны друг к другу.
- Параллельные грани: Соседние грани параллелепипеда параллельны друг другу.
- Равные противоположные грани: Параллельные грани параллелепипеда равны друг другу в площади.
- Равные противоположные ребра: Ребра, соединяющие противоположные вершины параллелепипеда, равны между собой в длине.
Параллелепипед используется в геометрии и в различных областях науки и техники, таких как архитектура, инженерия и физика. Изучение его свойств и особенностей позволяет решать задачи, связанные с вычислениями объема, площади поверхности, и определением взаимного положения граней и ребер.
Перпендикулярность в геометрии: определение и основные характеристики
Основной характеристикой перпендикулярности является ее свойство сохраняться при повороте и смещении. Если две линии или плоскости перпендикулярны, то они останутся такими же даже после поворота или смещения.
Перпендикулярность часто используется для решения геометрических задач, например, для нахождения высоты треугольника или построения пересечения прямой и плоскости. Также она играет важную роль в различных областях, таких как архитектура, инженерия и физика.
| Примеры перпендикулярных линий и плоскостей: |
|---|
| Два отрезка, которые пересекаются под прямым углом: |
| Две перпендикулярные плоскости, задаваемые уравнениями: |
| Плоскость 1: ax + by + cz + d1 = 0 |
| Плоскость 2: ax + by + cz + d2 = 0 |
Важно отметить, что перпендикулярность может быть обратной. Если два отрезка или плоскости образуют прямой угол друг с другом, они считаются перпендикулярными. Если же угол между ними не равен 90 градусов, они называются неперпендикулярными.
Способы доказательства перпендикулярности отрезка
Перпендикулярность отрезка DC в параллелепипеде ABCDA1B1C1D1 может быть доказана разными способами. Ниже представлены два основных способа доказательства:
1. Использование свойств параллелограмма:
Для доказательства перпендикулярности отрезка DC можно воспользоваться свойствами параллелограмма. Параллелограмм ABCD имеет две парами параллельных сторон AB и CD, AC и BD. При этом диагонали AC и BD делятся пополам. Также известно, что противоположные стороны параллелограмма равны по длине.
Таким образом, отрезок DC является диагональю параллелограмма ABCD и делится пополам точкой O. В свою очередь, точка O является серединой отрезка AB.
Из свойств параллелограмма следует, что диагонали параллелограмма пересекаются в точке, делящей их пополам и образующей прямой угол. Таким образом, отрезок DC перпендикулярен стороне AB параллелепипеда.
2. Использование свойства проекций в прямоугольных треугольниках:
Другим способом доказательства перпендикулярности отрезка DC является использование свойств проекций в прямоугольных треугольниках.
Если провести из точек A и D перпендикуляры на прямой отрезок DC, то получатся два прямоугольных треугольника: прямоугольный треугольник ABC и прямоугольный треугольник D1C1O.
Из свойства прямоугольных треугольников следует, что в таких треугольниках катеты, проведенные к прямому углу, являются высотой и основанием.
Таким образом, отрезок DC является основанием прямоугольного треугольника ABC, а отрезок D1C1 является высотой прямоугольного треугольника D1C1O.
Из свойства высоты и основания прямоугольного треугольника следует, что высота является перпендикуляром к основанию. Следовательно, отрезок DC перпендикулярен стороне AB параллелепипеда.
Общие признаки параллелепипедов и способы определения их перпендикулярности
Основными признаками параллелепипедов являются:
| Признак | Описание |
|---|---|
| Параллельность граней | У параллелепипеда все грани являются параллельными и попарно равными. |
| Прямолинейность ребер | Все ребра параллелепипеда являются прямолинейными отрезками. |
| Прямые углы | У параллелепипеда все углы являются прямыми углами. |
| Равные плоскости | Любые две противоположные грани параллелепипеда образуют плоскость, которая равна по площади. |
Перпендикулярность отрезка в параллелепипеде можно определить по следующим способам:
- Использование свойств векторного произведения. Если векторное произведение двух векторов, лежащих на отрезках, равно нулю, то отрезки перпендикулярны.
- Проверка на равенство длин отрезков. Если два отрезка, лежащих на сторонах параллелограмма, равны по длине, то они перпендикулярны.
- Использование формулы для определения угла между двумя векторами. Если угол между двумя векторами, лежащими на отрезках, равен 90 градусов, то отрезки перпендикулярны.
Доказательство перпендикулярности отрезка dc с помощью основных свойств параллелепипеда
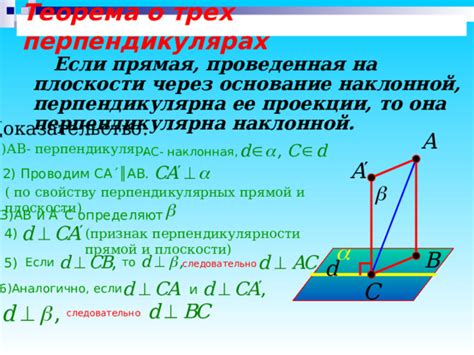
В данном случае рассмотрим грани abcd и a1b1c1d1. Они являются прямоугольниками, а их стороны ab и a1b1, bc и b1c1, ad и a1d1, dc и d1c1 являются параллельными.
Из основных свойств параллелепипеда следует, что прямые, соединяющие соответствующие вершины на противоположных гранях, перпендикулярны этим граням.
Таким образом, отрезок dc, соединяющий противоположные вершины на гранях abcd и a1b1c1d1, будет перпендикулярен этим граням.
Методы вычисления угла между отрезками
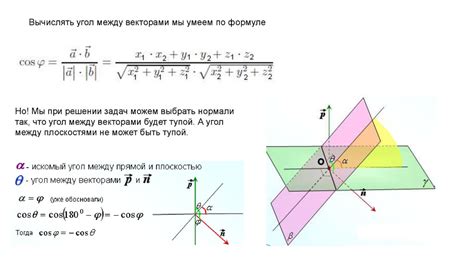
Для вычисления угла между отрезками можно использовать различные методы. Рассмотрим некоторые из них:
1. Формула косинусов.
Если известны длины отрезков и длина их общего отрезка, то угол между ними можно вычислить с помощью формулы косинусов:
cos(α) = (b^2 + c^2 - a^2) / (2 * b * c)
где α - угол между отрезками, a, b, c - длины отрезков.
2. Скалярное произведение векторов.
Если даны координаты начальных и конечных точек отрезков, угол между ними можно вычислить с помощью скалярного произведения векторов:
cos(α) = (AB * CD) / (|AB| * |CD|)
где α - угол между отрезками, AB - вектор, соединяющий начальную и конечную точки первого отрезка, CD - вектор, соединяющий начальную и конечную точки второго отрезка, |AB| и |CD| - длины этих векторов.
3. Теорема косинусов.
Если известны длины сторон треугольника, в котором лежат отрезки, и длины отрезков, угол между ними можно вычислить с помощью теоремы косинусов:
cos(α) = (b^2 + c^2 - a^2) / (2 * b * c)
где α - угол между отрезками, a, b, c - длины сторон треугольника.
Одним из этих методов можно найти угол между отрезками dc в параллелепипеде abcda1b1c1d1 и доказать его перпендикулярность.
Алгоритм построения перпендикуляра
Для построения перпендикуляра нужно выполнить следующие шаги:
1. Взять отрезок dc, который требуется проверить на перпендикулярность.
2. Найти середину отрезка dc и обозначить ее точкой m.
3. Найти вектор, соединяющий точки a и m. Обозначить его вектором am.
4. Найти вектор, соединяющий точки d и m. Обозначить его вектором dm.
5. Вычислить скалярное произведение векторов am и dm.
6. Если скалярное произведение равно нулю, то отрезок dc перпендикулярен плоскости a1b1c1d1.
7. Если скалярное произведение не равно нулю, то отрезок dc не перпендикулярен плоскости a1b1c1d1.
Таким образом, алгоритм позволяет определить перпендикулярность отрезка dc в параллелепипеде abcda1b1c1d1.
Практические примеры и задачи на доказательство перпендикулярности отрезка dc
Пример 1:
Рассмотрим параллелепипед abcda1b1c1d1. Известно, что отрезок ab паралленен отрезку c1d1. Построим отрезок dd1. Докажем, что отрезок dd1 перпендикулярен отрезку dc.
Решение: Для доказательства перпендикулярности отрезков dd1 и dc используем определение перпендикулярности. Если отрезки перпендикулярны, то их скалярное произведение равно нулю. Расчет скалярного произведения даст нам результат, подтверждающий перпендикулярность отрезков.
Пример 2:
В параллелепипеде abcda1b1c1d1 проведены отрезки ab и c1d1, пересекающиеся в точке e. Докажите, что отрезок dc перпендикулярен отрезку ae2.
Решение: В данной задаче также используется определение перпендикулярности отрезков через скалярное произведение. Нужно найти векторы, соответствующие отрезкам dc и ae2, и расчитать их скалярное произведение. Если оно равно нулю, то отрезки перпендикулярны.
Задача 1:
В параллелепипеде abcda1b1c1d1 проведены отрезки ab и d1d2, пересекающиеся в точке e. Найдите условие, при котором отрезок d2c1 будет перпендикулярен отрезку ae.
Решение: Чтобы отрезок d2c1 был перпендикулярен отрезку ae, нужно, чтобы их скалярное произведение было равно нулю. Получив это условие, мы сможем найти соответствующие координаты точек.



