Перпендикулярность диагоналей четырехугольника – это свойство, при котором диагонали этой фигуры пересекаются под прямым углом. То есть, если мы проведем прямые, соединяющие противоположные вершины, то они пересекутся в точке, образуя два прямых угла. Для доказательства этого свойства мы воспользуемся понятием векторов.
Вектор – это математический объект, который характеризует направление и величину движения в пространстве. В данной задаче мы будем использовать двумерные векторы, которые представляются с помощью двух чисел – координат. Координаты вектора обозначаются как (x, y), где x – это горизонтальная составляющая, а y – вертикальная составляющая вектора. Используя свойства векторов, мы сможем доказать перпендикулярность диагоналей четырехугольника.
Диагонали четырехугольника
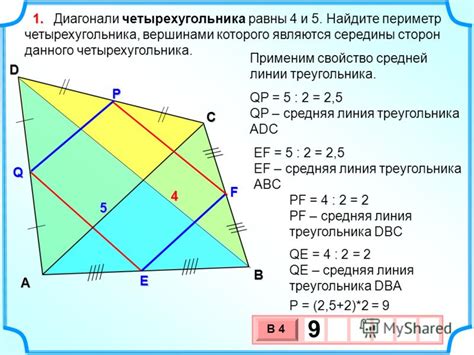
Чтобы доказать перпендикулярность диагоналей четырехугольника, можно воспользоваться понятием вектора.
Вектор - это математический объект, характеризующийся направлением и величиной. Векторы могут служить инструментом для описания геометрических конструкций, таких как диагонали.
Применяя понятие вектора к четырехугольнику, для доказательства перпендикулярности его диагоналей, нужно установить, что вектор, соединяющий середины диагоналей, перпендикулярен одной из диагоналей.
Для этого обозначим вершины четырехугольника как A, B, C и D, а середины диагоналей как M и N. Проведем векторы AB, BC, CD и DA, а также векторы AM и BN.
Если векторы AM и BN перпендикулярны одной из диагоналей, то их скалярное произведение будет равно нулю:
- AM · AB = 0
- BN · BC = 0
- CM · CD = 0
- DN · DA = 0
Если выражения AM · AB = 0 и BM · BA = 0 истинны, то это означает, что векторы AM и BN перпендикулярны диагонали AC. Таким образом, мы доказали перпендикулярность диагонали AC и одной из ее серединных пересекающихся диагоналей.
Аналогично можно доказать перпендикулярность диагонали BD и ее серединной пересекающейся диагонали.
Таким образом, через векторы можно доказать перпендикулярность диагоналей четырехугольника.
Определение и свойства

Диагональ - это отрезок, соединяющий две несоседние вершины четырехугольника.
Перпендикулярность диагоналей четырехугольника - это особое свойство, при котором диагонали пересекаются в точке, и образуют прямые углы друг с другом.
Для доказательства перпендикулярности диагоналей четырехугольника можно использовать векторный подход. Вектор - это математический объект, который характеризуется направлением и длиной.
С помощью векторов мы можем задать диагонали четырехугольника и проверить, что их скалярное произведение равно нулю. Если скалярное произведение диагоналей равно нулю, то это означает, что диагонали перпендикулярны друг другу.
Таким образом, векторный метод позволяет нам доказать перпендикулярность диагоналей четырехугольника с использованием математических операций с векторами.
Положение четырехугольника
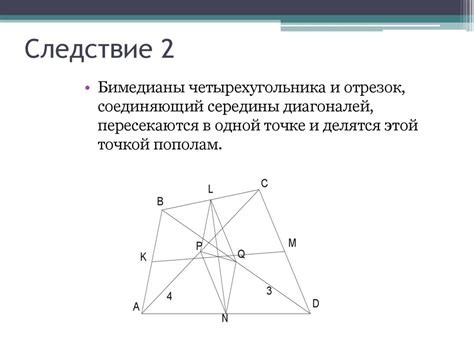
Положение четырехугольника можно описать при помощи координат вершин. Для этого можно задать координаты каждой вершины в виде упорядоченных пар чисел (x, y), где x - координата по горизонтали, y - координата по вертикали.
Также положение четырехугольника можно описать при помощи векторов. Вектор - это направленный отрезок, который содержит информацию о его длине и направлении. При задании положения четырехугольника через векторы используются векторы, соединяющие вершины четырехугольника.
Положение четырехугольника может быть различным: остроугольным, тупоугольным или прямоугольным. Также четырехугольник может быть выпуклым или невыпуклым. В зависимости от положения его диагоналей можно определить, является ли четырехугольник параллелограммом, квадратом или прямоугольником.
Рассмотрим четырехугольник ABCD. Если его диагонали AC и BD перпендикулярны, то четырехугольник ABCD называется перпендикулярным. Векторные методы позволяют доказать, что диагонали перпендикулярны путем сравнения векторных произведений AB и CD с нулем.
Перпендикулярность диагоналей
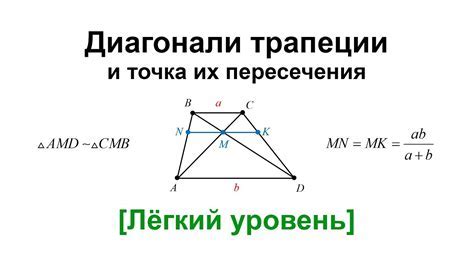
Для доказательства перпендикулярности диагоналей в четырехугольнике через векторы необходимо использовать определение перпендикулярности и алгебраический подход.
Пусть дан четырехугольник ABCD, где точки A, B, C и D являются вершинами четырехугольника, а точки AC и BD - его диагонали.
Векторче BA будет направлен от A к B, а вектор BA - от B к A. Аналогичные обозначения используются для остальных векторов.
Используя свойства векторов, можно записать, что сумма векторов AB и BC равна вектору AC: AB + BC = AC.
Аналогично, сумма векторов BA и AD будет равна вектору BD: BA + AD = BD.
Заметим, что эти два уравнения образуют систему уравнений с двумя неизвестными векторами AB и BC.
Если предположить, что диагонали AC и BD перпендикулярны, то векторы AC и BD будут ортогональными, что означает, что их скалярное произведение равно нулю: AC · BD = 0.
Раскрывая скалярное произведение и подставляя значения векторов, получим следующее выражение: (AB + BC) · (BA + AD) = 0.
Раскрывая скобки и группируя слагаемые, получим: AB · BA + AB · AD + BC · BA + BC · AD = 0.
Учитывая, что AB · BA = |AB|² и BC · BA = 0 (перпендикулярные векторы), уравнение примет вид: |AB|² + AB · AD = 0.
Таким образом, мы получили, что сумма квадрата длины вектора AB и скалярного произведения векторов AB и AD равна нулю.
Это возможно только в случае, когда векторы AB и AD являются ортогональными, то есть перпендикулярными.
Таким образом, мы доказали, что если диагонали AC и BD перпендикулярны, то векторы AB и AD также перпендикулярны.
Обратно, если векторы AB и AD перпендикулярны, то по тем же шагам можно показать, что диагонали AC и BD также перпендикулярны.
Таким образом, мы доказали перпендикулярность диагоналей в четырехугольнике через векторы.
Взаимное положение векторов
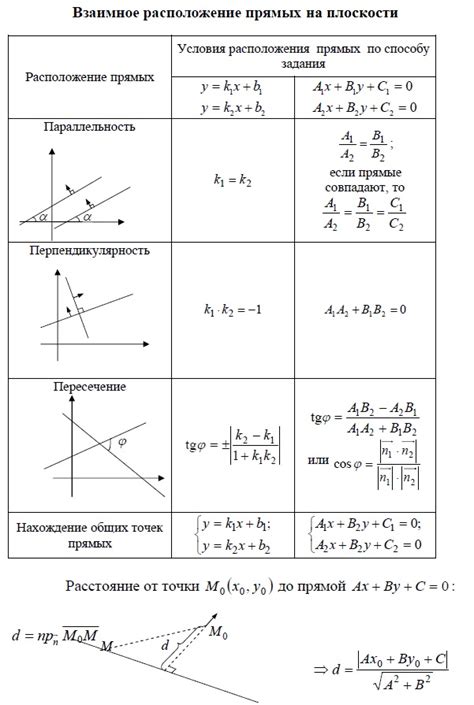
Векторы могут находиться в различных взаимных положениях. Рассмотрим основные случаи:
- Коллинеарные векторы: если два вектора лежат на одной прямой или параллельны друг другу, они являются коллинеарными.
- Перпендикулярные векторы: векторы, которые образуют прямой угол друг с другом, называются перпендикулярными.
- Диагональные векторы: если вектор делит другой вектор пополам, они называются диагональными.
- Компланарные векторы: векторы, лежащие в одной плоскости, называются компланарными.
Доказательство через векторы
Для доказательства перпендикулярности диагоналей четырехугольника можно воспользоваться методом векторных вычислений. Для этого нам понадобятся знания о свойствах векторов и основных операциях над ними.
Пусть у нас есть четырехугольник ABCD, и нам нужно доказать, что его диагонали AC и BD перпендикулярны. Чтобы это сделать, мы будем использовать условие перпендикулярности двух векторов, которое гласит: если скалярное произведение двух векторов равно нулю, то они перпендикулярны.
Вектор AB мы можем выразить, используя координаты его концов:
AB = B - A
Аналогично, вектор CD можно записать как:
CD = D - C
Теперь мы можем найти скалярное произведение этих двух векторов:
AB · CD = (B - A) · (D - C)
Обозначим координаты точек A(x1, y1), B(x2, y2), C(x3, y3) и D(x4, y4). Тогда мы можем вычислить складывание и вычитание соответствующих координат:
AB · CD = (x2 - x1, y2 - y1) · (x4 - x3, y4 - y3)
По свойствам скалярного произведения, мы можем рассмотреть его как сумму произведений соответствующих координат:
AB · CD = (x2 - x1) * (x4 - x3) + (y2 - y1) * (y4 - y3)
Если скалярное произведение равно нулю, то получается следующее уравнение:
(x2 - x1) * (x4 - x3) + (y2 - y1) * (y4 - y3) = 0
Если мы докажем, что это уравнение выполняется для нашего четырехугольника ABCD, то это будет означать, что его диагонали перпендикулярны.
Таким образом, мы доказали перпендикулярность диагоналей четырехугольника ABCD с помощью векторных вычислений.
Примеры четырехугольников
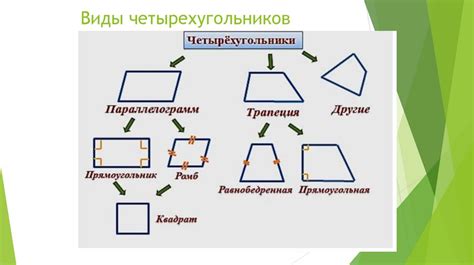
1. Прямоугольник: Это четырехугольник, у которого все углы прямые (равны 90 градусам). Два противоположных угла и две противоположные стороны равны между собой.
2. Квадрат: Это четырехугольник, у которого все стороны равны между собой и все углы прямые (равны 90 градусам). Все его диагонали равны и перпендикулярны друг другу.
3. Ромб: Это четырехугольник, у которого все стороны равны между собой, но не все углы прямые. Диагонали ромба перпендикулярны друг другу и делят его на четыре равных треугольника.
4. Трапеция: Это четырехугольник, у которого две стороны параллельны друг другу, а две другие - не параллельны. Диагонали трапеции не обязательно перпендикулярны между собой.
Это лишь несколько примеров четырехугольников, их разнообразие бесконечно. Каждый четырехугольник обладает своими уникальными свойствами и может иметь различные комбинации углов и сторон.



