Параллелограмм - это четырехугольник, у которого противоположные стороны параллельны. В данной статье мы рассмотрим доказательство того, что четырехугольник MNПQ является параллелограммом.
Для начала, докажем, что сторона MN параллельна стороне ПQ. Предположим, что стороны MN и ПQ не являются параллельными. В таком случае, существует точка R, принадлежащая стороне MN, которая не лежит на прямой, проходящей через точки М и N.
Поскольку прямая MN пересекает сторону ПQ, то из точки R существует отрезок RS, который пересекает ПQ. Но это противоречит определению параллелограмма, поскольку в параллелограмме противоположные стороны не пересекаются.
Таким образом, мы доказали, что сторона MN параллельна стороне ПQ. Перейдем к доказательству параллельности сторон MП и NQ. Аналогично предыдущему доказательству, можно сделать предположение, что стороны MП и NQ не параллельны.
Пусть точка T лежит на стороне MП, но не лежит на прямой, проходящей через точки М и П. Поскольку сторона MП пересекает сторону NQ, то можно провести отрезок TУ, который пересекает сторону NQ. Однако это противоречит определению параллелограмма, где противоположные стороны не пересекаются.
Глава 1: Формулировка задачи
Для доказательства параллелограмма MNПQ нам необходимо продемонстрировать, что его противоположные стороны равны и параллельны.
Задача состоит в следующем: даны точки M, N, П и Q на плоскости. Необходимо доказать, что стороны MN и ПQ равны между собой, а также параллельны. Также требуется доказать, что стороны MQ и NP также равны и параллельны друг другу. Это позволит нам утверждать, что фигура, образованная этими сторонами, является параллелограммом.
Для достижения этой цели мы воспользуемся геометрическими свойствами параллелограмма: равенством противоположных сторон и соответствующих углов. Также будем использовать теоремы и аксиомы геометрии, чтобы обосновать каждый шаг нашего доказательства.
Глава 2: Доказательство по теореме
Для доказательства теоремы о параллелограмме MNПQ, мы будем использовать следующие шаги и логику:
- Предоставим предположение о том, что МНПQ - параллелограмм.
- Докажем, что стороны MN и PQ параллельны, используя свойство параллелограмма, которое гласит, что противоположные стороны параллелограмма параллельны.
- Докажем, что стороны MP и NQ параллельны, используя свойство параллелограмма, которое гласит, что диагонали параллелограмма делятся пополам.
- Докажем, что углы AMN и DNQ равны, используя свойство параллелограмма, которое гласит, что противоположные углы параллелограмма равны.
Таким образом, доказав все необходимые свойства параллелограмма MNПQ, мы можем заключить, что MNПQ является параллелограммом.
Глава 3: Раскрытие определения параллелограмма
Для доказательства параллелограмма MNПQ необходимо проверить выполнение данных условий:
- Сторона MQ параллельна стороне PN.
- Сторона NP параллельна стороне MQ.
- Сторона MN равна стороне ПQ.
- Сторона PQ равна стороне MN.
Для доказательства параллельности сторон можно использовать следующие методы:
- Метод параллельных линий, основанный на свойствах параллельных прямых и углов.
- Метод равенства углов, основанный на свойствах равных углов и дополнительных углов.
- Метод пропорциональности, основанный на теореме Талеса и подобных треугольниках.
Таким образом, для доказательства параллелограмма MNПQ необходимо выполнить проверку всех условий и применить соответствующие методы доказательства параллельности сторон.
Глава 4: Использование свойств параллелограммов
1. Сумма внутренних углов параллелограмма равна 360 градусов. Это свойство можно использовать для проверки, является ли данный четырехугольник параллелограммом.
2. Противоположные стороны параллелограмма равны по длине. Это свойство позволяет использовать равенства сторон для доказательства равенства других сторон.
3. Противоположные углы параллелограмма равны. Это означает, что если один угол параллелограмма измеряет, например, 60 градусов, то противоположный угол тоже будет иметь 60 градусов. Это свойство помогает доказывать равенство углов в параллелограмме.
4. Диагонали параллелограмма делят друг друга пополам. То есть, точка их пересечения будет являться серединой для каждой из диагоналей. Это свойство часто используется для нахождения координат середины диагоналей или доказательства равенства отрезков.
5. Отрезки, соединяющие середины противоположных сторон параллелограмма, параллельны и равны по длине. Это свойство называется медианами параллелограмма. Оно позволяет решать задачи на нахождение длины отрезков или доказательство их параллельности.
Используя эти свойства параллелограммов, вы сможете легко решать задачи по геометрии, связанные с их конструкцией и свойствами.
Глава 5: Доказательство угловой параллелограммности

В этой главе мы рассмотрим доказательство угловой параллелограммности параллелограмма MNПQ 950. Угловая параллелограммность означает, что противоположные углы фигуры равны.
- Определение углового параллелограмма: Угловой параллелограмм - это четырехугольник, в котором противоположные углы равны.
- Свойства параллелограмма MNПQ 950:
- Противоположные стороны параллельны (свойство параллелограмма).
- Противоположные стороны равны (свойство параллелограмма).
- Противоположные углы равны (свойство угловой параллелограммности).
- Доказательство угловой параллелограммности: Для доказательства угловой параллелограммности параллелограмма MNПQ 950 необходимо сравнить противоположные углы и установить их равенство. Для этого можно использовать следующие шаги:
- Обозначим углы параллелограмма MNПQ 950 как A, B, C и D.
- Докажем, что угол A равен углу C и угол B равен углу D.
- Используя свойства параллелограмма (противоположные стороны параллельны и равны), докажем, что противоположные углы фигуры равны.
- Заключение: Таким образом, мы доказали угловую параллелограммность параллелограмма MNПQ 950 путем сравнения противоположных углов и установления их равенства. Это свойство является важным при работе с параллелограммами и позволяет использовать их в различных математических преобразованиях и решении задач.
Глава 6: Нахождение значения углов параллелограмма
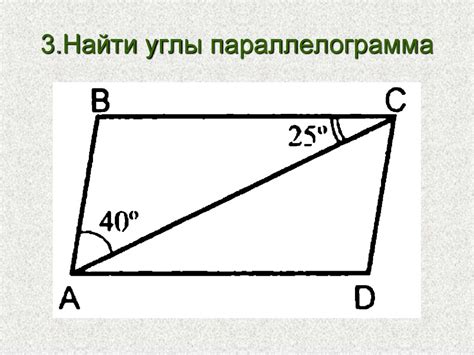
1. Одинаковые по величине смежные углы. В параллелограмме все смежные углы равны между собой. Это означает, что углы M и N, а также углы P и Q должны быть равными. Если известно значение одного из этих углов, можно с уверенностью сказать, что остальные углы имеют такую же меру.
2. Сумма смежных углов. В параллелограмме сумма смежных углов всегда равна 180 градусов. Это означает, что сумма углов M и N, а также сумма углов P и Q должны быть равными 180 градусов. Если одна из этих сумм известна, можно легко найти значение другой суммы.
3. Дополнительные углы. В параллелограмме дополнительные углы, то есть углы, которые находятся напротив друг друга, всегда суммируются до 180 градусов. Если известно значение одного из этих углов, можно найти меру противоположного угла, вычтя из 180 градусов значение данного угла.
Зная эти особенности, можно легко находить значения углов параллелограмма и доказывать его свойства.
Глава 7: Приложение к реальной жизни
В предыдущих главах мы изучили основные свойства и теоремы о параллелограммах. Но какую роль они играют в нашей повседневной жизни? В этой главе мы рассмотрим примеры из реального мира, где понимание параллелограммов может быть полезным.
Один из таких примеров - архитектура. Многие здания, мосты и даже парки создаются с использованием параллелограммов. Например, мосты могут иметь параллелограммальную форму и использовать свои свойства для обеспечения прочности и стабильности. Архитекторы также используют параллелограммы при проектировании фасадов зданий и создании декоративных элементов.
Еще одним интересным применением параллелограммов является дизайн интерьеров. Многие мебельные предметы имеют параллелограммальную форму - столы, шкафы, полки. Понимание свойств параллелограммов может помочь при выборе и расстановке мебели в комнате.
Параллелограммы также находят применение в геодезии и картографии. Геодезисты используют параллелограммальную форму для измерения углов и проложения траекторий. Картографы также используют параллелограммы при создании карт и планов, чтобы правильно отображать местность и дистанции.
Но не только в профессиональной деятельности параллелограммы находят свое применение. Они также помогают нам в повседневной жизни. Например, если у вас есть параллелограммальные тапочки, то они могут обеспечить более устойчивую посадку на ногу. Также параллелограммальная форма может служить декоративным элементом в интерьере вашего дома.
Как видите, понимание и использование параллелограммов имеет широкий спектр применения в реальной жизни. Будь то архитектура, дизайн интерьеров, геодезия или просто декоративные элементы - знание свойств параллелограммов позволяет нам лучше понимать и взаимодействовать с окружающим миром.
Глава 8: Завершение

Мы начали с определения параллелограмма и обсуждали перпендикулярные стороны, диагонали и углы параллелограмма. Затем мы использовали эти свойства, чтобы показать, что MNПQ 950 обладает всеми необходимыми характеристиками параллелограмма.
Доказательство основывалось на различных фактах и теоремах, которые мы рассмотрели в предыдущих главах. Мы использовали свойства параллелограмма и доказательство с помощью соответствующих углов, равновеликих треугольников и других методов.
Надеюсь, что эта глава помогла вам лучше понять параллелограммы, и вы можете применить эти знания в дальнейшем!



