Диаграммы Эйлера – это графический способ визуализации соотношения элементов в заданном множестве. Их разработал знаменитый швейцарский математик Леонард Эйлер. Эти диаграммы служат отличным инструментом для объяснения сложных концепций или показа взаимодействия между различными категориями данных.
Основной принцип диаграмм Эйлера – использование пересекающихся кругов для показа совпадений или отличий между элементами. Каждый круг представляет собой отдельную категорию, а пересечение кругов – совместно принадлежащие элементы нескольким категориям одновременно.
Диаграммы Эйлера широко применяются в различных областях, включая науку, статистику, бизнес-аналитику и информационную графику. С их помощью можно исследовать и анализировать любые данные с несколькими переменными, представляя информацию в простой и понятной форме.
Диаграммы Эйлера: новый способ отображения соотношения элементов

Эти диаграммы могут быть полезными для визуализации данных и выявления зависимостей или трендов между элементами. Они могут использоваться в различных областях, таких как бизнес-анализ, маркетинг, научное исследование и даже в образовании.
Преимущества использования диаграмм Эйлера заключаются в их простоте и эффективности. Они помогают легко визуализировать сложные данные и делают их более понятными для аудитории. Кроме того, диаграммы Эйлера могут быть интерактивными, что позволяет наблюдателю получать более глубокое понимание представленных данных.
Для создания диаграммы Эйлера необходимо выбрать подходящие элементы, которые нужно отобразить, и определить их относительные размеры. Затем можно использовать специальные инструменты или программное обеспечение для создания диаграммы.
Один из способов создания диаграммы Эйлера - использование програмного обеспечения, такого как Microsoft Excel или Google Sheets. С помощью этих программ можно создать круглую диаграмму и разделить ее на сегменты в соответствии с относительными размерами элементов.
Другим способом создания диаграммы Эйлера является использование специализированных онлайн-инструментов или программ, таких как Lucidchart или Canva. Эти инструменты обеспечивают большую гибкость и функциональность при создании диаграмм и позволяют добавить различные стили и визуальные эффекты.
Проблемы с традиционными графиками
Традиционные графики, такие как столбчатые, линейные или круговые диаграммы, имеют свои преимущества при отображении данных, но они также имеют свои ограничения и проблемы.
Одной из основных проблем с традиционными графиками является их ограничение на отображение только двух переменных. Например, столбчатая диаграмма может показать соотношение между двумя категориями данных, но не может показать более двух категорий или взаимосвязь между ними.
Еще одной проблемой является сложность интерпретации данных на графиках. В зависимости от выбранного масштаба осей, график может давать искаженное представление данных. Кроме того, некоторые типы графиков могут быть сложными для восприятия, особенно для людей без опыта работы с ними.
Традиционные графики также могут быть неэффективными при отображении больших объемов данных. Например, на линейной диаграмме может быть трудно визуализировать множество точек данных, особенно если они сгруппированы близко друг к другу.
И наконец, традиционные графики обычно не позволяют отображать сложные взаимосвязи или зависимости между элементами данных. Например, они не могут показать, какие элементы данных принадлежат нескольким категориям одновременно или какие элементы влияют на другие.
Для решения этих проблем некоторые исследователи и профессионалы в области визуализации данных используют диаграммы Эйлера. Эти диаграммы позволяют визуализировать сложные взаимосвязи между элементами данных и отображать больше чем две переменные. Они также могут быть более понятными и эффективными при отображении больших объемов данных.
| Изображение: | Пример диаграммы Эйлера |
В чем преимущества диаграмм Эйлера
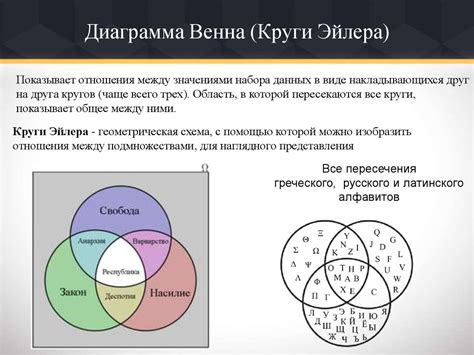
Одним из основных преимуществ диаграмм Эйлера является их простота и интуитивность. Даже неопытные пользователи смогут легко понять, как интерпретировать диаграмму и извлечь из нее нужную информацию.
Другим важным преимуществом диаграмм Эйлера является их способность компактно представлять множество данных. Благодаря использованию пересекающихся кругов или эллипсов, диаграммы Эйлера могут вместить большое количество категорий или подкатегорий, что делает их удобными для анализа сложных систем или процессов.
Диаграммы Эйлера также позволяют выделить общие и уникальные элементы в наборе данных. Просто сравнивая размеры сегментов и их пересечения, можно определить, какие элементы присутствуют только в одной категории и какие элементы соединяют различные категории.
Одной из ключевых особенностей диаграмм Эйлера является их гибкость. Их можно использовать для представления разных типов данных, таких как процентное соотношение, количественные значения или категории. При необходимости можно легко добавить новые категории или подкатегории и обновить диаграмму, что делает их универсальным инструментом для визуализации данных.
| Преимущества диаграмм Эйлера |
|
Практическое применение диаграмм Эйлера
Вот несколько практических примеров использования диаграмм Эйлера:
- Маркетинг: диаграммы Эйлера могут быть использованы для отображения доли рынка различных продуктов или услуг, уровня узнаваемости бренда или успешности маркетинговых кампаний. Это помогает представить информацию о конкурентной среде и принять решение о настройке маркетинговой стратегии.
- Управление проектами: диаграммы Эйлера могут быть использованы для идентификации основных компонентов проекта и определения их взаимной связи. Также они позволяют оценить степень завершенности каждого компонента и определить критические точки, которые следует уделить особое внимание.
- Бизнес-анализ: диаграммы Эйлера могут быть использованы для анализа данных о прибыли, расходах или объемах продаж по различным категориям. Это помогает выявить преобладающие факторы успеха и принять решение о распределении ресурсов.
- Научные исследования: диаграммы Эйлера могут быть использованы для визуализации результатов экспериментов или исследований. Они позволяют наглядно представить соотношение между различными переменными и выделить наиболее значимые зависимости.
Практическое применение диаграмм Эйлера зависит от конкретной задачи и области применения. Их гибкость и удобство использования делают их неотъемлемым инструментом для работы с данными в различных сферах деятельности.
Шаги по созданию диаграммы Эйлера

Шаг 1: Определите элементы и их соотношение.
Первым шагом в создании диаграммы Эйлера является определение элементов, которые вы хотите включить в диаграмму, и их соотношение. Элементы могут быть частями целого или представлять собой отдельные категории.
Шаг 2: Нарисуйте контур основы диаграммы.
Следующим шагом является рисование контура основы диаграммы. Основа диаграммы Эйлера обычно представляет собой эллипс или окружность, которая будет служить границей для элементов диаграммы.
Шаг 3: Закрасьте области для каждого элемента.
После того, как вы нарисовали контур основы диаграммы, вы можете приступить к закрашиванию областей для каждого элемента. Каждая область представляет собой отдельный сегмент, который соответствует определенному элементу диаграммы.
Шаг 4: Добавьте текст и легенду.
Чтобы сделать диаграмму Эйлера более понятной, можно добавить текстовые метки для каждого элемента и легенду, которая объясняет, что представляет собой каждый сегмент диаграммы.
Шаг 5: Разместите процентное соотношение.
Дополните диаграмму Эйлера, разместив процентное соотношение для каждого элемента. Это поможет читателям лучше понять долю каждого элемента в общей картины.
Шаг 6: Проверьте и откорректируйте диаграмму.
Наконец, перед публикацией или использованием диаграммы Эйлера рекомендуется проверить ее на наличие ошибок и внесении необходимых корректировок. Убедитесь, что текст читаем, процентные соотношения точны и легенда понятна.
Следуя этим шагам, вы сможете создать информативную диаграмму Эйлера, которая ясно отобразит соотношение между элементами и поможет вам лучше понять представленные данные.
В данной статье мы рассмотрели использование диаграмм Эйлера для отображения соотношения элементов. Было продемонстрировано, как создавать диаграммы Эйлера с помощью кода и инструментов, таких как Python и Matplotlib.
Мы узнали, что диаграммы Эйлера являются эффективным способом визуализации соотношения между элементами, особенно в случаях, когда элементы пересекаются между собой. При помощи таких диаграмм легко определить наличие общих элементов и их объединение.
Кроме того, были рассмотрены основные принципы создания диаграмм Эйлера, включая выбор соответствующих данных, настройку размеров и цветов диаграммы, а также добавление подписей и легенды.
Отметим, что диаграммы Эйлера могут быть использованы в различных областях, таких как маркетинг, исследования данных, биология и связанные с ними области. Они помогают наглядно представить сложные данные и делают процесс анализа более понятным и удобным.



