Дизъюнкция – это логическая операция, которая представляет собой объединение двух или более высказываний. В результате дизъюнкции получается новое высказывание, которое становится истинным в том случае, если хотя бы одно из исходных высказываний истинно.
Для наглядности можно использовать таблицу истинности, чтобы рассмотреть все возможные комбинации значений исходных высказываний и результат дизъюнкции:
Высказывание A | Высказывание B | Дизъюнкция A OR B
Истинно | Истинно | Истинно
Истинно | Ложно | Истинно
Ложно | Истинно | Истинно
Ложно | Ложно | Ложно
Давайте рассмотрим примеры, чтобы лучше понять, как работает дизъюнкция. Предположим, у нас есть два высказывания: "Сегодня солнечно" и "Сегодня ветрено". Если мы объединим эти два высказывания с помощью дизъюнкции, то получим новое высказывание: "Сегодня солнечно или сегодня ветрено". Это высказывание будет истинным, если хотя бы одно из исходных высказываний истинно. То есть, если сегодня и солнечно, и ветрено, высказывание "Сегодня солнечно или сегодня ветрено" будет также истинным.
Таким образом, дизъюнкция позволяет учесть несколько возможных вариантов истинности высказывания и получить более полное представление о логической связи между двумя или более высказываниями.
Таблица истинности дизъюнкции высказывания
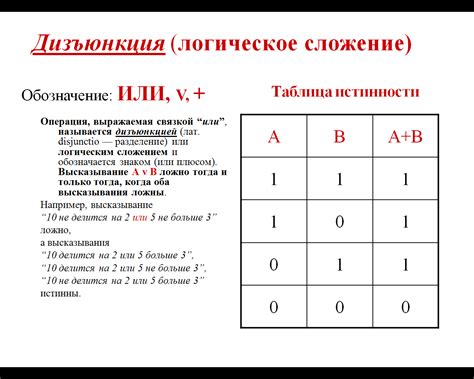
Таблица истинности дизъюнкции высказывания представляет собой способ систематизации и анализа полученных результатов в зависимости от различных комбинаций значений истинности для двух высказываний.
В случае дизъюнкции, которая обозначается символом "или" (v), имеется два высказывания A и B. Таблица истинности содержит четыре возможных комбинации:
- Оба высказывания A и B истинны (A и B)
- Высказывание A истинно, а B ложно (A и не B)
- Высказывание A ложно, а B истинно (не A и B)
- Оба высказывания A и B ложны (не A и не B)
Значение истинности дизъюнкции определено следующим образом:
- Если хотя бы одно из высказываний A и B истинно, то дизъюнкция также будет истинной.
- Только в случае, когда оба высказывания A и B ложны, дизъюнкция становится ложной.
Для лучшего понимания приведем примеры:
- Если "Сегодня солнечный день" и "Сегодня день недели - суббота", то дизъюнкция "Сегодня солнечный день или сегодня день недели - суббота" истинна, так как оба высказывания истинны.
- Если "Вкусный пирог" и "Кофе без сахара", то дизъюнкция "Вкусный пирог или кофе без сахара" истинна, так как первое высказывание истинно.
- Если "Автобус пришел вовремя" и "Поезд опоздал", то дизъюнкция "Автобус пришел вовремя или поезд опоздал" истинна, так как второе высказывание истинно.
- Если "Экзамен был сложным" и "Студент не готовился", то дизъюнкция "Экзамен был сложным или студент не готовился" ложна, так как оба высказывания ложны.
Определение и примеры

Таблица истинности для дизъюнкции содержит четыре возможных комбинации двух высказываний:
| Высказывание A | Высказывание B | Дизъюнкция (A V B) |
|---|---|---|
| Истина (T) | Истина (T) | Истина (T) |
| Истина (T) | Ложь (F) | Истина (T) |
| Ложь (F) | Истина (T) | Истина (T) |
| Ложь (F) | Ложь (F) | Ложь (F) |
В примере:
Высказывание A: Сегодня солнечно.
Высказывание B: Сегодня дождь.
Дизъюнкция (A V B): Сегодня солнечно ИЛИ сегодня дождь.
Если хотя бы одно из высказываний истинно, то дизъюнкция также будет истинной.
Составление таблицы истинности
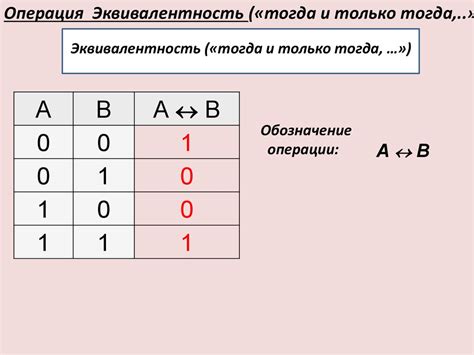
Для составления таблицы истинности дизъюнкции высказывания необходимо рассмотреть все возможные комбинации значений пропозициональных переменных, участвующих в дизъюнкции. После этого нужно определить истинностное значение самой дизъюнкции для каждой комбинации.
Предположим, у нас есть две пропозициональные переменные A и B, принимающие значения 0 или 1. Тогда возможные комбинации значений для этих переменных будут следующими:
| A | B |
|---|---|
| 0 | 0 |
| 0 | 1 |
| 1 | 0 |
| 1 | 1 |
Далее, для каждой комбинации значений переменных A и B определяем истинностное значение дизъюнкции A или B.
Например, при значениях A=0 и B=0 дизъюнкция A или B принимает значение 0. Определяя истинностное значение дизъюнкции для каждой комбинации значений переменных, получим следующую таблицу истинности:
| A | B | A или B |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Таким образом, таблица истинности для дизъюнкции высказывания A или B будет состоять из четырех строк, соответствующих всем возможным комбинациям значений переменных, и трех столбцов: столбец для значения переменной A, столбец для значения переменной B и столбец для значения дизъюнкции A или B.
Применение в логике и математике

В логике дизъюнкция высказывания позволяет объединять утверждения с помощью "или". Например, если у нас есть два утверждения: "сегодня солнечно" и "сегодня дождь", то дизъюнкция позволит нам объединить эти утверждения в одно: "сегодня солнечно или сегодня дождь". Это позволяет рассматривать различные комбинации утверждений и исследовать их логические свойства.
В математике дизъюнкция также широко используется. Например, она может быть применена для объединения двух множеств или для определения суммы двух чисел. Дизъюнктивная нормальная форма (ДНФ) – это один из основных способов представления логических функций с помощью дизъюнкции.
Дизъюнкция высказывания играет важную роль в логике и математике, позволяя анализировать и объединять утверждения, выражать логические связи и решать различные задачи. Она является неотъемлемой частью этих наук и используется во множестве различных контекстов и приложений.



