Дисперсия - это одна из наиболее фундаментальных и важных концепций в математике и статистике. Она позволяет измерять разброс значений в наборе данных и определить, насколько эти значения отклоняются от среднего значения. Дисперсия может быть полезна во многих областях, включая физику, экономику, социологию и многие другие.
Прежде чем мы погрузимся в детали, давайте рассмотрим простой пример, чтобы лучше понять, что такое дисперсия. Представьте, что вы замерили температуру воздуха в течение нескольких дней и получили следующие значения: 25, 24, 23, 26, 25. Чтобы вычислить дисперсию, сначала нужно найти среднее значение - в данном случае оно равно 24.6.
Далее, мы должны вычислить разницу каждого значения среднего значения и возведенную разницу в квадрат. В нашем примере, разницы между значениями и средним равны: 0.4, -0.6, -1.6, 1.4, 0.4. Затем мы возводим эти разницы в квадрат: 0.16, 0.36, 2.56, 1.96, 0.16.
Что такое дисперсия в математике?

Дисперсия является одной из основных характеристик, используемых для описания статистических данных. Она позволяет определить, насколько данные однородны или разнородны и какие из них могут быть репрезентативными для выборки.
Для вычисления дисперсии, нужно вычислить квадратичное отклонение каждого элемента данных от их среднего значения, затем сложить все квадратичные отклонения и разделить их на общее количество элементов данных. Математическое представление формулы дисперсии:
| Формула дисперсии: | $$\sigma^2 = \frac{\sum_{i=1}^{n}(x_i - \bar{x})^2}{n}$$ |
|---|
Где:
- $$\sigma^2$$ - дисперсия
- $$x_i$$ - каждый отдельный элемент данных
- $$\bar{x}$$ - среднее значение данных
- $$n$$ - общее количество элементов данных
Чем больше дисперсия, тем больше разброс данных. Маленькая дисперсия указывает на меньший разброс и более однородные данные. Значение дисперсии всегда будет неотрицательным числом, так как мы возводим разницу между элементами данных и их средним значением в квадрат.
Определение дисперсии
Для вычисления дисперсии необходимо выполнить следующие шаги:
- Вычислить среднее значение выборки - это сумма всех значений, деленная на количество значений.
- Вычислить разность каждого значения в выборке и среднего значения.
- Возвести каждую разность в квадрат.
- Вычислить сумму квадратов разностей.
- Разделить сумму квадратов разностей на количество значений в выборке минус один. Это даст нам дисперсию.
Дисперсия обычно обозначается символом σ² (сигма в квадрате) или VAR.
Вычисление дисперсии позволяет анализировать величину разброса данных и определить, насколько значительны отклонения от среднего значения. Большая дисперсия указывает на больший разброс данных в выборке, а маленькая дисперсия указывает на меньший разброс.
Формула расчета дисперсии
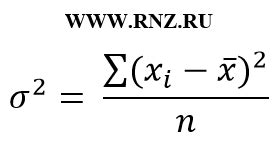
Дисперсия (σ^2) = Сумма ( (Значение - Математическое ожидание)^2 ) / Количество значений
В данной формуле:
- σ^2 обозначает дисперсию
- Значение представляет отдельное значение случайной величины
- Математическое ожидание представляет собой среднее значение случайной величины
- Сумма означает суммирование всех значений
- Количество значений представляет собой количество значений случайной величины
Полученное значение дисперсии будет показывать, насколько значения случайной величины отклоняются от их среднего значения. Чем больше полученное значение дисперсии, тем больше разброс значений и наоборот.
Примеры использования дисперсии

| Область | Пример использования |
|---|---|
| Финансы | Для оценки риска и волатильности инвестиций. Более высокая дисперсия означает более нестабильные и рискованные инвестиции, в то время как более низкая дисперсия указывает на более стабильные и предсказуемые инвестиции. |
| Наука | В экспериментах и исследованиях для измерения степени разброса данных. Дисперсия позволяет узнать, насколько точные и надежные результаты эксперимента. |
| Программирование | В алгоритмах и моделях для оценки качества работы программного кода. Дисперсия может помочь идентифицировать участки кода, которые вызывают нестабильности и ошибки. |
| Образование | Для оценки успеваемости студентов. При сравнении результатов тестов или экзаменов, дисперсия может указывать на то, насколько разнообразны оценки студентов и какие учебные материалы или методики необходимо улучшить. |
Это только несколько примеров использования дисперсии, и в реальной жизни она находит применение во многих других областях, где необходимо измерить разброс данных и оценить степень неопределенности.



