В математике понятие "вертикальные углы" играет важную роль при изучении геометрии. Оно относится к основным понятиям в области углов и помогает решать различные задачи, связанные с измерением углов и определением их свойств.
Вертикальные углы определяются в плоскости, когда две прямые линии пересекаются друг с другом. Важной особенностью вертикальных углов является то, что их значения равны друг другу. Это значит, что если два угла образуются при пересечении прямых, то они будут иметь одинаковую величину и считаться вертикальными углами.
Для определения свойств вертикальных углов необходимо знать основные правила геометрии. Если у нас есть два угла, образованных пересечением двух прямых, и мы предполагаем, что они являются вертикальными, то для доказательства этого можно использовать различные методы. Например, можно использовать аксиому, утверждающую, что вертикальные углы всегда равны друг другу.
Также существует несколько других способов определения вертикальных углов. Например, по заданию можно найти две прямые линии, пересечение которых образует углы, и затем проверить равенство этих углов. Если они окажутся равными, то это будут вертикальные углы.
Вертикальные углы: основные понятия и определения

Простым примером вертикального угла является угол, который образуется при расщеплении от прямого угла. Другими словами, когда вертикальная линия пересекает горизонтальную на примерно нижней половине, она образует два угла: прямой угол и вертикальный угол.
Свойства вертикальных углов:
1. Вертикальные углы всегда равны между собой. Это означает, что если угол А равен углу Б, то угол В также будет равен углу А.
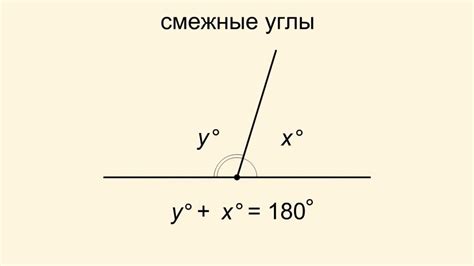
2. Сумма вертикальных углов всегда равна 180 градусам. Например, если угол А равен 40 градусам, то угол Б будет составлять 140 градусов, чтобы в сумме с углом А получилось 180 градусов.
Примеры использования вертикальных углов:
1. При построении геометрических фигур и вычислении их свойств.
2. В инженерии и строительстве для определения углов наклона или накрена поверхностей.
3. В физике и астрономии для измерения углов и определения направления.
4. В школьной математике для решения геометрических задач и упражнений.
Теперь, имея понятие о вертикальных углах и их свойствах, можно успешно использовать их в решении математических задач и более глубоком понимании пространственных отношений. Удачи в изучении геометрии!
Что такое вертикальные углы и как они образуются
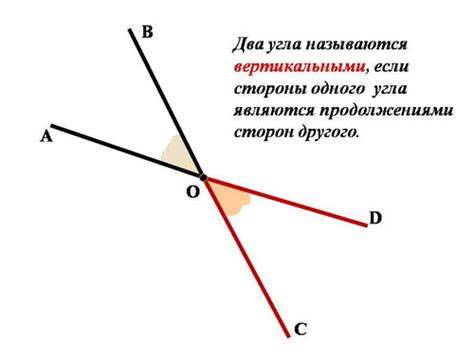
Вертикальные углы образуются при пересечении двух прямых линий, когда две параллельные прямые линии пересекаются третьей перпендикулярной прямой. При этом вертикальные углы будут располагаться по разные стороны от перпендикулярной линии и иметь равные значения. Вертикальные углы всегда состоят из противоположных друг другу углов, и их мера всегда равна.
Основным свойством вертикальных углов является то, что они всегда равны друг другу. Если два угла являются вертикальными, то их меры будут одинаковыми и равняться друг другу. Это значит, что если один угол имеет меру, например, 60 градусов, то второй угол, являющийся вертикальным к нему, также будет иметь меру 60 градусов.
Вертикальные углы широко применяются в геометрии и могут быть использованы для решения различных задач, связанных с измерением углов и конструированием фигур. Понимание свойств вертикальных углов позволяет легче решать геометрические задачи и строить правильные конструкции.
Свойства вертикальных углов: равенство имерность
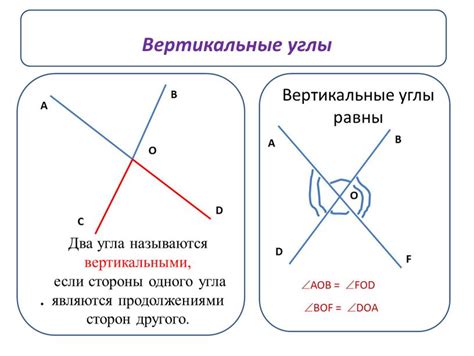
Если две прямые линии пересекаются, то вертикальные углы, образованные этим пересечением, будут равными. Это означает, что их меры (величины) будут одинаковыми.
Например, пусть имеются прямые AB и CD, пересекающиеся в точке O. Тогда угол AOC и угол BOD будут вертикальными углами и, соответственно, их меры будут равными.
Свойство равенства имерность вертикальных углов часто используется для решения геометрических задач, так как оно позволяет находить значения углов, зная лишь меры некоторых других углов или свойства фигур.
Запомните, что вертикальные углы всегда равны между собой, что делает их важным инструментом в геометрии и позволяет строить точные и точные вычисления углов.
Методы определения вертикальных углов

Определение вертикальных углов может быть достаточно простым, если вам известна информация о пересекающихся прямых или поворачивающихся линиях.
Существует несколько методов, которые позволяют определить свойства вертикальных углов:
- Метод сравнения: доказательство вертикальности двух углов можно осуществить, сравнивая их значения. Если значения углов одинаковы, то они вертикальные.
- Метод измерения: при наличии инструментов для измерения углов, можно использовать их для определения степени разницы между двумя углами. Если разница равна нулю, углы вертикальные.
- Метод доказательства: иногда можно доказать вертикальность углов с помощью геометрических свойств и теорем. Например, если две прямые пересекаются и образуют углы, у которых сумма равна 180 градусам, то они вертикальные.
- Метод параллельности: если две прямые параллельны, любые пересекающие их линии будут образовывать вертикальные углы.
Используя эти методы определения вертикальных углов, вы сможете с легкостью находить и анализировать такие углы в геометрических фигурах и конструкциях.
Работа с вертикальными углами: использование в геометрии

В геометрии, вертикальные углы занимают особое место и играют важную роль при решении задач. Знание свойств вертикальных углов позволяет определить равенство или разность значений углов и применять их в различных ситуациях.
Вертикальные углы - это углы, образованные пересечением двух прямых линий. Они расположены по разные стороны пересекающихся прямых, но имеют одинаковую меру. Другими словами, два вертикальных угла всегда равны друг другу.
Однако, следует помнить, что вертикальные углы могут быть лишь частью решения задачи, и иногда требуется использовать другие свойства углов и фигур для полного решения задачи.
Итак, работа с вертикальными углами является важной частью геометрии и может быть использована для определения равенства углов, доказательства теорем и решения различных задач.
Особенности вертикальных углов в различных фигурах

Однако, стоит отметить, что особенности вертикальных углов зависят от типа фигур, в которых они встречаются. Рассмотрим несколько примеров:
| Фигура | Описание вертикальных углов |
|---|---|
| Прямая линия | Если две прямые линии пересекаются, то все углы, образованные этой пересечением, являются вертикальными. Все вертикальные углы имеют одинаковую величину и равны 90 градусам. |
| Прямоугольник | В прямоугольнике все углы являются прямыми, следовательно, они все являются вертикальными. Все вертикальные углы в прямоугольнике равны 90 градусам. |
| Треугольник | Вертикальные углы в треугольнике могут быть равными, если одна из сторон треугольника параллельна другой. В противном случае, вертикальные углы в треугольнике имеют различные величины. |
| Пересечение прямых линий | Когда две прямые линии пересекаются, в точке пересечения образуется два пары вертикальных углов. Вертикальные углы, входящие в одну пару, равны между собой, но отличаются от вертикальных углов, входящих в другую пару. |
Таким образом, понимание особенностей вертикальных углов в различных фигурах позволяет легче определять их свойства и использовать их при решении геометрических задач.
Значение вертикальных углов в архитектуре и дизайне
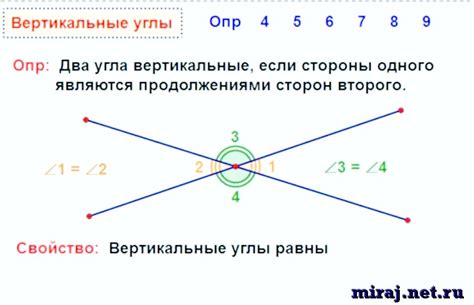
Вертикальные углы используются для создания прямых линий, которые могут быть использованы как ориентир для построения здания или объекта дизайна. Они также могут быть использованы для создания визуальных эффектов, добавляя глубину и объемность в пространстве.
Кроме того, вертикальные углы помогают определить пропорции и масштабы объектов, таких как стены, окна, двери и мебель. Они влияют на восприятие размеров и формы объектов, а также создают эффект перспективы и гармонии.
Например, в архитектуре вертикальные углы могут использоваться для создания впечатления высоты и грандиозности здания. Высокие и узкие вертикальные углы могут подчеркнуть вертикальность здания, а широкие и низкие вертикальные углы могут создать ощущение устойчивости и мощи.
В дизайне интерьера вертикальные углы могут использоваться для создания определенного настроения или стиля помещения. Например, вертикальные углы с острыми углами могут придавать помещению ощущение динамичности и энергии, в то время как вертикальные углы с закругленными краями могут создавать ощущение комфорта и безопасности.
Определить свойства и значение вертикальных углов в архитектуре и дизайне можно путем изучения принципов композиции, анализа пространственных взаимоотношений и экспериментирования с различными формами и углами.
Полезные приложения для изучения и измерения вертикальных углов
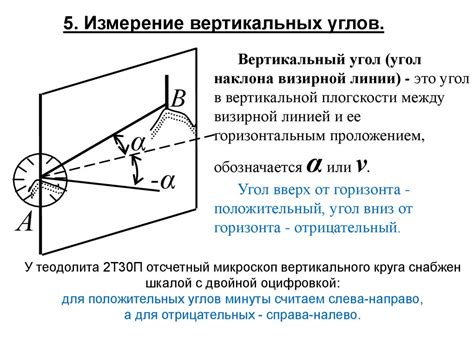
- Угломер: это приложение для смартфонов, которое позволяет измерять углы с помощью встроенных акселерометра и гироскопа. Оно позволяет быстро и легко определить вертикальные углы, а также измерить наклон поверхности.
- Угломер Pro: это расширенная версия приложения "Угломер", которая предлагает дополнительные функции, такие как сохранение измерений, преобразование различных единиц измерения и создание графиков для анализа угловых данных.
- Геодезический инструмент: это приложение, которое предлагает широкий спектр функций для измерения углов и расстояний. Оно может использоваться не только для изучения вертикальных углов, но и для выполнения сложных геодезических расчетов.
- Компас: многие приложения компаса для смартфонов также позволяют измерять углы. Они предоставляют возможность определить направление и угол наклона с помощью встроенного магнетометра и акселерометра.
Эти приложения являются полезными инструментами для изучения и измерения вертикальных углов. Они позволяют быстро и точно определить углы, их величину, а также производить различные вычисления связанные с геометрией и строительством.
Интересные факты о вертикальных углах и их применение в жизни
Как можно применить знание о вертикальных углах в жизни? Одно из практических применений этого понятия - измерение вертикальных углов с помощью угломера. Угломеры используются в строительстве и геодезии для определения угловых величин, а также для создания точных карт и планов местности.
Вертикальные углы также играют важную роль в навигации и ориентировании. Пары вертикальных углов могут использоваться для определения направления и точного местоположения объектов.
Еще один интересный факт о вертикальных углах заключается в их применении в геометрии и математике. Понимание свойств и связей вертикальных углов помогает решать задачи по геометрии и алгебре, а также в различных областях науки и техники.
| Свойства вертикальных углов |
|---|
| Вертикальные углы равны друг другу |
| Сумма мер вертикальных углов равна 180 градусам |
Изучение вертикальных углов помогает не только в понимании геометрических форм и применении их в практике, но и развивает логическое мышление и аналитические навыки. Знание свойств вертикальных углов может быть полезно не только для будущих математиков и инженеров, но и для обычных людей, в повседневной жизни.



