Вершина треугольника - это одна из основных понятий, которое учат детей в третьем классе математики. Треугольник - это геометрическая фигура, которая состоит из трех сторон и трех углов.
Каждый треугольник имеет три вершины, которые являются точками пересечения его сторон. Вершины обозначаются буквами, чаще всего как A, B и C. Благодаря вершинам треугольника можно определить его форму и свойства.
Например, если в треугольнике одна из вершин имеет угол 90 градусов, то такой треугольник называется прямоугольным. Если все три угла треугольника острые, то он является остроугольным, а если один из углов тупой, то треугольник называется тупоугольным.
Знание понятия "вершина треугольника" позволяет детям правильно определять и классифицировать различные треугольники, что является важным навыком в изучении геометрии.
Вершина треугольника: понятие и свойства
У треугольника всегда три вершины, каждая из которых образуется при пересечении двух сторон. Вершины треугольника обозначаются заглавными буквами латинского алфавита, например, A, B и C.
Вершина А образуется пересечением сторон BC и AC, вершина B - сторон AB и BC, а вершина C - сторон AB и AC.
Свойства вершин треугольника:
- Все вершины треугольника лежат на одной плоскости.
- Любые две вершины треугольника можно соединить отрезком, который будет являться стороной треугольника.
- Три вершины треугольника не лежат на одной прямой.
- Может быть только одна вершина в одной точке.
Определение вершины треугольника

Для обозначения вершин треугольника используется следующая система координат. Каждая вершина обозначается парой чисел (x, y), где x - горизонтальная координата, а y - вертикальная координата. Координаты вершин могут быть положительными, отрицательными или равными нулю.
Вершины треугольника могут быть использованы для вычисления его периметра, площади и других характеристик. Они также определяют форму и положение треугольника в пространстве.
| Вершина | Обозначение |
|---|---|
| Вершина A | (xA, yA) |
| Вершина B | (xB, yB) |
| Вершина C | (xC, yC) |
Знание координат вершин треугольника позволяет проводить точные геометрические расчеты и работать с этой фигурой на плоскости.
Как найти вершину треугольника
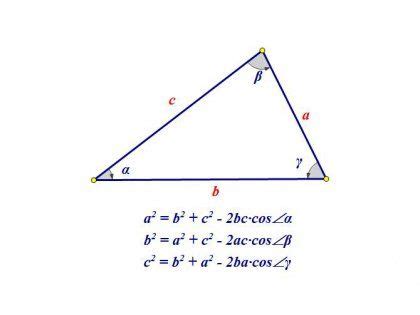
Для нахождения вершины треугольника можно воспользоваться различными методами, в зависимости от доступных данных:
- Если даны координаты всех трех вершин треугольника, можно просто найти нужную вершину по известным координатам.
- Если даны длины всех сторон треугольника и координаты одной из его вершин, можно воспользоваться формулой нахождения координат других вершин.
Найденная вершина треугольника может быть использована для решения различных математических задач, например, вычисления площади треугольника, нахождения периметра и других характеристик.
Свойства вершины треугольника

- Каждая вершина определяет две стороны треугольника. Например, вершина A определяет стороны AB и AC.
- Три вершины треугольника образуют его углы. Углы треугольника обозначаются соответствующими буквами вершин. Например, угол BAC образован вершинами B, A и C.
- Вершина треугольника может также указывать на его положение. Если треугольник расположен в плоскости, вершина может указывать на его направление или ориентацию.
Таким образом, вершина треугольника имеет важную роль в его определении и свойствах. Она помогает определить стороны треугольника, его углы и положение в пространстве.



