Геометрия – это наука о формах, размерах и отношениях фигур. Одним из важных понятий в геометрии является угол. Угол – это область плоскости, ограниченная двумя лучами, которые имеют общее начало. Углы бывают различных видов: острые, прямые, тупые и т. д. В этой статье мы рассмотрим, что такое тупой угол.
Тупой угол – это угол, который имеет величину больше 90 градусов и меньше 180 градусов. Тупой угол можно представить себе как угол, который "смотрит назад". Он выглядит шире и менее заостренным, чем острый угол, и не может быть вписан в прямую.
В геометрии тупой угол играет важную роль. Прежде всего, он является противоположностью острому углу. Острые и тупые углы вместе составляют полный угол, равный 180 градусов. Также тупой угол используется для классификации треугольников. Если в треугольнике есть хотя бы один тупой угол, то такой треугольник называется тупоугольным.
Тупой угол: свойства и примеры, полное объяснение

Свойства тупого угла:
- Тупой угол всегда имеет меру больше 90 градусов и меньше 180 градусов.
- Линии, образующие тупой угол, продолжаются за пределы угла и не пересекаются внутри него.
- Если два угла смежные и один из них тупой, то сумма их мер равна 180 градусов.
- Если тупой угол выложен как продолжение продолжения другого угла, то эти углы называются смежными углами.
- Угол, который имеет значение меньше 90 градусов, называется острый, а имеющий меру равную 90 градусам – прямой угол.
Примеры тупых углов:
- Угол, составленный сторонами прямоугольного треугольника, кроме прямого угла.
- Угол, составленный стрелками на часах в момент, когда они образуют угол, превышающий половину круга (180 градусов).
- Угол, образованный линиями, пересекающимися внутри окружности и образующий "затупление" этой окружности.
- Угол, составленный двумя прямыми линиями, образующими "разворот" в противоположных направлениях.
Тупые углы широко используются в геометрии и имеют множество приложений в повседневной жизни. Понимание и использование тупых углов полезно для решения геометрических задач и конструирования различных фигур и конструкций.
Определение и характеристики тупого угла в геометрии
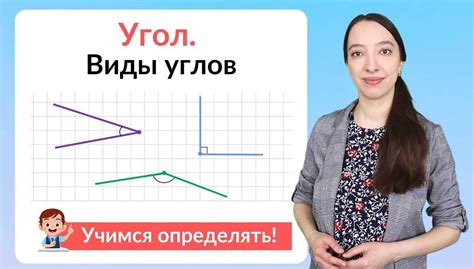
Тупой угол - это угол, значение которого больше 90 градусов и меньше 180 градусов. Можно представить тупой угол, как если бы два луча разводились в стороны, в противоположные направления, на таком расстоянии, что между ними образовывается угол, больше прямого угла (90 градусов), но меньше угла поворота на полный круг (180 градусов).
Характеристики тупого угла включают:
- Величину. Тупой угол имеет значение больше 90 градусов и меньше 180 градусов.
- Форму. Тупой угол имеет внешний вид, похожий на открытый полукруг или часть круга.
- Свойства. Тупой угол не может быть прямым или острым, так как его величина превышает 90 градусов.
- Перпендикулярность. Для тупого угла характерно то, что его стороны не являются перпендикулярными друг другу, а образуют угол больше 90 градусов.
Тупые углы находят широкое применение в геометрии и в реальном мире. Они могут использоваться для измерения углов поворота или для создания фигур и конструкций с заданным углом. Тупые углы также являются важными элементами в различных математических и научных концепциях.
Примеры и изображение тупого угла на плоскости
Примеры тупых углов включают замыкание дверей, распростертую ладонь или основание буквы "L" на клавиатуре. Представим, что мы устанавливаем дверь и угол между дверной панелью и плоскостью стены составляет 220°. Такой угол является примером тупого угла.
На плоскости тупой угол обозначается дугой или маркером, чтобы обозначить движение от одного конца отрезка к другому в положительном направлении. Изображение тупого угла на плоскости представлено ниже:
<изображение тупого угла с подписью, объясняющей его меру в градусах и описание объекта, для которого угол является примером тупого угла>
Свойства и особенности тупого угла, объяснение и доказательства
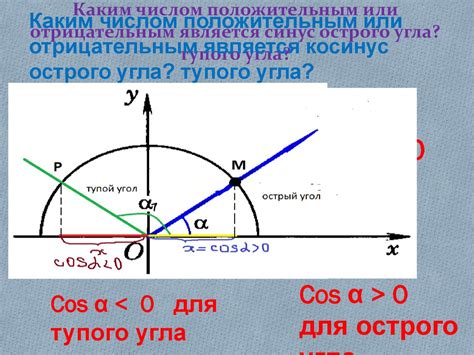
Одним из основных свойств тупого угла является то, что его мера всегда больше 90 градусов и меньше 180 градусов. Это означает, что две его стороны лежат в разных полуплоскостях.
Одним из способов объяснить это свойство является рассмотрение треугольника, в котором один из углов является тупым. Если мы возьмем две его стороны, лежащие в разных полуплоскостях, и продолжим их, то они никогда не пересекутся.
Тупой угол можно также доказать с помощью абсолютного значения синуса угла. Синус тупого угла всегда положителен и меньше 1, что свидетельствует о его большей мере, но меньшей, чем полный угол.
Еще одним свойством тупого угла является его дополнение, которое является остроугольным. То есть, если мы возьмем тупой угол и его дополнение, их сумма всегда будет равна 180 градусов.
Свойства и особенности тупого угла демонстрируют его уникальные характеристики в геометрии. Понимание и использование этих свойств помогает в решении задач и построении различных фигур.



